DE-BOOK Units, Mass, Volume, Concentration

Section Units, Mass, Volume, Concentration

[provisional cross-reference: WORK-IN-PROGRESS]

We’re about to start working on applications involving mixing solutions in tanks. That means we need to be mindful of units (for example--we can’t add miles and kilograms), mass balance, and volumes. We also can develop some intuition that will be helpful when we tackle more complicated questions.

🔗

Consider the equation \(s \cdot X = d,\) where \(s\) is a speed and has units of miles/hour. The variable \(d\) represents distance and has units miles. What units must the variable \(X\) have?
🔗

Solution.

In order to make the unit analysis work,

\begin{equation*} \ub{s}_{\frac{\text{mi}}{\text{hr}}}\cdot \ub{X}_{?} = \ub{d}_{\text{mi}}, \end{equation*}

we would need \(X\) to have units of hours.

🔗

🔗

Answer.

hours
🔗

🔗

🔗
Consider the equation \(A = B \cdot C,\) where \(A\) has units of moles/hour and \(B\) has units of gallons/hour. What must the units of \(C\) be?
🔗

Solution.

In order to make the unit analysis work,

\begin{equation*} \ub{A}_{\frac{\text{moles}}{\text{hr}}} = \ub{B}_{\frac{\text{gal}}{\text{hr}}} \cdot \ub{C}_{?}, \end{equation*}

we would need \(C\) to have units of moles/gallon.

🔗

🔗

Answer.

moles/gallon
🔗

🔗

🔗
Consider the equation \(M - N\cdot P = Z,\) where \(M\) has units of ft\(\cdot\)lb/sec, \(N\) has units of ft, \(P\) has units of lb/sec. What must the units of \(Z\) be?
🔗

Solution.

In order to make the unit analysis work,

\begin{equation*} \ub{M}_{\frac{\text{ftlb}}{\text{sec}}} - \ub{N}_{\text{ft}} \cdot \ub{P}_{\frac{\text{lb}}{\text{sec}}} = \ub{Z}_{?}, \end{equation*}

we would need \(Z\) to have units of ft\(\cdot\)lb/sec.

🔗

🔗

Answer.

ft\(\cdot\)lb/sec
🔗

🔗

🔗
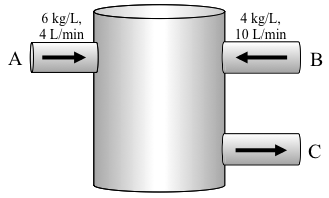
Consider the tank below, which has salt water solutions (also called brines) entering via two input lines (A and B) and has one output line (C).

🔗

🔗
If the tank level does not change, what volumetric flow rate must be leaving via the output line C?
🔗

Solution.

Brine is entering the tank at volumetric flow rate

\begin{equation*} 4 \text{L/min} + 10 \text{L/min} = 14 \text{L/min}. \end{equation*}

Since the tank level does not change, brine must leave at the same rate, 14 L/min.

🔗

🔗

Answer.

14 L/min
🔗

🔗

🔗
The concentration (in kg/L) of salt in each brine solution is shown in the figure. At what rate (in kg/min) is salt entering the tank?
🔗

Solution.

Salt is entering the tank via inlet A at a rate

\begin{equation*} 4 \frac{\text{L}}{\text{min}} \times 6 \frac{\text{kg}}{\text{L}} = 24 \frac{\text{kg}}{\text{min}}. \end{equation*}

Similarly, salt enters via inlet B at a rate

\begin{equation*} 10 \frac{\text{L}}{\text{min}} \times 4 \frac{\text{kg}}{\text{L}} = 40 \frac{\text{kg}}{\text{min}}. \end{equation*}

Altogether, then, salt enters at a rate of 64 kg/min.

🔗

🔗

Answer.

64 kg/min
🔗

🔗

🔗
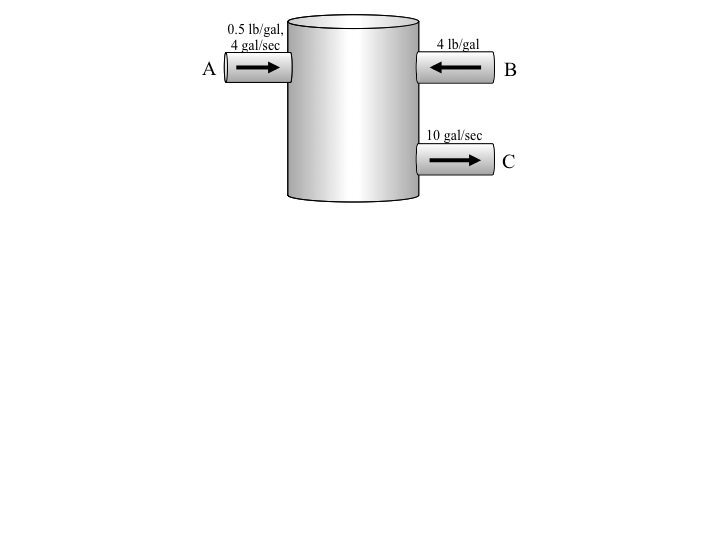
Consider the tank below, which has liquid entering via two input lines (A and B) and has one output line (C).

🔗

🔗
If the tank level does not change, what volumetric flow rate must be entering via the input line B?
🔗

Solution.

Brine is leaving the tank at volumetric flow rate 10 gal/sec. Inlet A contributes 4 gal/sec, which means that if the tank level is to remain constant, inlet B must contribute 6 gal/sec.
🔗

🔗

Answer.

6 gal/sec
🔗

🔗

🔗
The concentration (in lb/gal) of salt in each brine solution is shown in the figure. Assuming the tank level doesn’t change, at what rate (in lb/sec) is salt entering the tank?
🔗

Solution.

Salt is entering the tank via inlet A at a rate

\begin{equation*} 4 \frac{\text{gal}}{\text{sec}} \times 0.5 \frac{\text{lb}}{\text{gal}} = 2 \frac{\text{lb}}{\text{sec}}. \end{equation*}

Similarly, salt enters via inlet B at a rate

\begin{equation*} 6 \frac{\text{gal}}{\text{sec}} \times 4 \frac{\text{lb}}{\text{gal}} = 24 \frac{\text{lb}}{\text{sec}}. \end{equation*}

Altogether, then, salt enters at a rate of 26 lb/sec.

🔗

🔗

Answer.

26 lb/sec
🔗

🔗

🔗
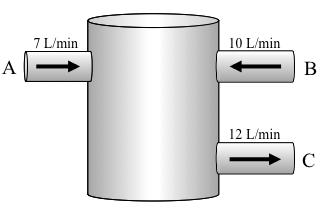
Consider the tank below, which has liquid entering via two input lines (A and B) and has one output line (C).

🔗

🔗
What happens to the level of the tank over time? Be specific.
🔗

Solution.

Liquid is entering at a rate of 7+10 = 17 L/min. It leaves at a rate of 12 L/min. That means that the amount of liquid in the tank increases at a rate of 5 L/min.
🔗

🔗

Answer.

increases (volume increases at a rate of 5 L/min)
🔗

🔗

🔗
If the tank has a capacity of 1500 L, and is empty at time \(t = 0\) minutes, write a function \(V(t)\) for volume of liquid in the tank at time \(t\) minutes.
🔗

Solution.

Since the amount of liquid in the tank increases at a rate of 5 L/min, we have

\begin{align*} V(t) \amp = \ub{\text{(initial volume)}}_{L} + \ub{\text{(rate)}}_{\frac{\text{L}}{\text{min}}} \times\ub{\text{(time)}}_{\text{min}} \\ \amp = 0 + 5t \end{align*}

Since the capacity of the tank is 1500 L, this equation only works for \(0 \le t \le 300\) minutes.

🔗

🔗

Answer.

\begin{equation*} V(t) = 5t, \hspace{1cm} 0 \le t \le 300 \end{equation*}

🔗

🔗

🔗
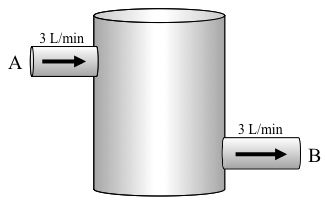
Consider the tank below, which has liquid entering via one input line (A) and is drained via one output line (B).

🔗

🔗
Suppose the tank initially contains 50 L of water that is dark red due to food coloring and that the liquid entering the tank is pure water. Imagine that we allow the pure water to enter the tank and the mixed solution to drain out of the tank for a really long time; you can think about it happening for years, if it helps. What color would you expect the water in the tank to be after a really long time?
🔗

Solution.

Over time we would expect that the water in the tank is almost identical to the incoming fluid. Therefore, we expect the tank be clear (i.e., pure water).
🔗

🔗

Answer.

clear (i.e., pure water)
🔗

🔗

🔗
Suppose the tank initially contains 50 L of pure water and that the liquid entering the tank is water that is dark red due to food coloring. Imagine that we allow the dark red water to enter the tank and the mixed solution to drain out of the tank for a really long time; you can think about it happening for years, if it helps. What color would you expect the water in the tank to be after a really long time?
🔗

Solution.

Over time we would expect that the water in the tank is almost identical to the incoming fluid. Therefore, we expect the tank to have dark red water--the same as the incoming water.
🔗

🔗

Answer.

dark red (same as incoming water)
🔗

🔗

🔗
Consider the tank below, which has liquid entering via an input line (A) and is drained via one output line (B).
Suppose the tank initially contains 50 gallons of a salt water solution (also called a brine) with concentration 6 lb/gal, and that the liquid entering the tank is pure water.
🔗

🔗
How much salt is initially in the tank?
🔗

Solution.

Initially we have

\begin{equation*} 50 \text{ gal }\times 6 \frac{\text{lb}}{\text{gal}} = 300 \text{ lb.} \end{equation*}

🔗

🔗

Answer.

300 lb
🔗

🔗

🔗
Imagine that we allow the pure water to enter the tank and the mixed solution to drain out of the tank for a really long time; you can think about it happening for years, if it helps. What concentration of salt do you expect there to be in the tank after a long time?
🔗

Solution.

Initially we have salt in the tank, but over time, no salt is added but the solution is drained, so more and more salt leaves the tank. Over time we would expect that the concentration of salt would decrease to 0 lb/gal.
🔗

🔗

Answer.

0 lb/gal
🔗

🔗

🔗
How much salt do you expect to be in the tank after a long time? (Note that this is a slightly different question than the previous question.)
🔗

🔗
Consider the tank below, which has liquid entering via one input line (A) and is drained via one output line (B).
Suppose the tank initially contains 50 L of a brine with concentration 6 kg/L, and that the liquid entering the tank is a brine with concentration 8 kg/L.
🔗

🔗
Imagine that we allow the brine to enter the tank and the mixed solution to drain out of the tank for a really long time; you can think about it happening for years, if it helps. What concentration of salt do you expect there to be in the tank after a long time?
🔗

Solution.

Over time we would expect that the fluid in the tank is almost identical to the incoming fluid. Therefore, we expect the concentration of salt to be 8 kg/L.
🔗

🔗

Answer.

8 kg/L
🔗

🔗

🔗
How much salt do you expect to be in the tank after a long time? (Note that this is a slightly different than asking about the concentration of salt. Hint: use units!)
🔗

Solution.

Since we expect the concentration to be 8 kg/L, and there are 50 L of solution in the tank (which doesn’t change because the volumetric flow rate in is equal to the volumetric flow rate out), then we expect there will be

\begin{equation*} 8 \frac{\text{kg}}{\text{L}} \times 50 \text{ L} = 400 \text{ kg}. \end{equation*}

🔗

🔗

Answer.

400 kg
🔗

🔗

🔗

🔗

You have attempted of activities on this page.

🔗

Prev TopNext