Section 7.2 The Quadratic Formula
We have learned how to solve certain quadratic equations using the square root property. In this section, we will learn another method, the quadratic formula.
Subsection 7.2.1 Solving Quadratic Equations with the Quadratic Formula
The standard form for a quadratic equation is
\begin{equation*}
ax^2+bx+c=0
\end{equation*}
where \(a\) is some nonzero number.
When \(b=0\) and the equation’s form is \(ax^2+c=0\text{,}\) then we can simply use the square root property to solve it. For example, \(x^2-4=0\) leads to \(x^2=4\text{,}\) which leads to \(x=\pm2\text{,}\) a solution set of \(\{-2,2\}\text{.}\)
But can we solve equations where \(b\neq0\text{?}\) A general method for solving a quadratic equation is to use what is known as the quadratic formula.
Fact 7.2.2. The Quadratic Formula.
For any quadratic equation \(ax^2+bx+c=0\) where \(a\neq0\text{,}\) the solutions are given by
\begin{equation*}
x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}
\end{equation*}
As we have seen from solving quadratic equations, there can be at most two solutions. Both of the solutions are included in the quadratic formula with the \(\pm\) symbol. We could write the two solutions separately:
\begin{align*}
x=\frac{-b-\sqrt{b^2-4ac}}{2a}\amp\amp\text{ or }\amp\amp x=\frac{-b+\sqrt{b^2-4ac}}{2a}
\end{align*}
This method for solving quadratic equations will work to solve every quadratic equation. It is most helpful when \(b\ne0\).
Example 7.2.3.
Linh is in a physics class that launches a tennis ball from a rooftop that is \(90.2\) feet above the ground. They fire it directly upward at a speed of \(14.4\) feet per second and measure the time it takes for the ball to hit the ground below. We can model the height of the tennis ball, \(h\text{,}\) in feet, with the quadratic equation \(h=-16x^2+14.4x+90.2\text{,}\) where \(x\) represents the time in seconds after the launch. According to the model, when should the ball hit the ground? Round the time to one decimal place.
The ground has a height of \(0\) feet. Substituting \(0\) for \(h\) in the equation, we have this quadratic equation:
\begin{equation*}
0=-16x^2+14.4x+90.2
\end{equation*}
We cannot solve this equation with the square root property, so we will use the quadratic formula. First we will identify that \(\highlight{a=-16}\text{,}\) \(\highlight{b=14.4}\) and \(\highlight{c=90.2}\text{,}\) and substitute them into the formula:
\begin{align*}
x\amp=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\\
x\amp=\frac{-(\substitute{14.4})\pm\sqrt{(\substitute{14.4})^2-4(\substitute{-16})(\substitute{90.2})}}{2(\substitute{-16})}\\
x\amp=\frac{-14.4\pm\sqrt{207.36-(-5772.8)}}{-32}\\
x\amp=\frac{-14.4\pm\sqrt{207.36+5772.8}}{-32}\\
x\amp=\frac{-14.4\pm\sqrt{5980.16}}{-32}\\
\end{align*}
These are the exact solutions but because we have a context we want to approximate the solutions with decimals.
\begin{align*}
x\amp\approx-1.966\text{ or }x\approx2.866
\end{align*}
We don’t use the negative solution because a negative time does not make sense in this context. The ball will hit the ground approximately \(2.9\) seconds after it is launched.
The quadratic formula can be used to solve any quadratic equation, but it requires that you don’t make any slip-up with remembering the formula, that you correctly identify \(a\text{,}\) \(b\text{,}\) and \(c\text{,}\) and that you don’t make any arithmetic mistakes when you calculate and simplify. We recommend that you always check whether you can use the square root property before using the quadratic formula. Here is another example.
Example 7.2.4.
Solve for \(x\) in \(2x^2-9x+5=0\text{.}\)
Explanation.
First, we check and see that we cannot use the square root property (because \(b\neq0\)) so we will use the quadratic formula. Next we identify that \(\highlight{a=2}\text{,}\) \(\highlight{b=-9}\) and \(\highlight{c=5}\text{.}\) We substitute them into the quadratic formula:
\begin{align*}
x\amp=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\\
x\amp=\frac{-(\substitute{-9})\pm\sqrt{(\substitute{-9})^2-4(\substitute{2})(\substitute{5})}}{2(\substitute{2})}\\
x\amp=\frac{9\pm\sqrt{81-40}}{4}\\
x\amp=\frac{9\pm\sqrt{41}}{4}
\end{align*}
This is fully simplified because we cannot simplify \(\sqrt{41}\) or reduce the fraction. The solution set is \(\left\{\frac{9-\sqrt{41}}{4},\frac{9+\sqrt{41}}{4}\right\}\text{.}\) We do not have a context here so we leave the solutions in their exact form.
When a quadratic equation is not in standard form we must convert it before we can identify the values of \(a\text{,}\) \(b\) and \(c\text{.}\) We will show that in the next example.
Example 7.2.5.
Solve for \(x\) in \(x^2=-10x-3\text{.}\)
Explanation.
First, we convert the equation into standard form by adding \(10x\) and \(3\) to each side of the equation:
\begin{equation*}
x^2+10x+3=0
\end{equation*}
Next, we check that we cannot use the square root property so we will use the quadratic formula. We identify that \(\highlight{a=1}\text{,}\) \(\highlight{b=10}\) and \(\highlight{c=3}\text{.}\) We substitute them into the quadratic formula:
\begin{align*}
x\amp=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\\
x\amp=\frac{-\substitute{10}\pm\sqrt{(\substitute{10})^2-4(\substitute{1})(\substitute{3})}}{2(\substitute{1})}\\
x\amp=\frac{-10\pm\sqrt{100-12}}{2}\\
x\amp=\frac{-10\pm\sqrt{88}}{2}
\end{align*}
We notice that the radical can be simplified:
\begin{align*}
x\amp=\frac{-10\pm2\sqrt{22}}{2}\\
x\amp=\frac{-10}{2}\pm\frac{2\sqrt{22}}{2}\\
x\amp=-5\pm\sqrt{22}
\end{align*}
The solution set is \(\{-5-\sqrt{22}, -5+\sqrt{22}\}\text{.}\)
Remark 7.2.6.
The irrational solutions to quadratic equations can be checked, although doing so can sometimes involve a lot of simplification and is not shown throughout this section. As an example, to check the solution of \(-5+\sqrt{22}\) from Example 5, we would replace \(x\) with \(-5+\sqrt{22}\) and check that the two sides of the equation are equal. This check is shown here:
\begin{align*}
x^2\amp=-10x-3\\
(\substitute{-5+\sqrt{22}})^2\amp\wonder{=}-10(\substitute{-5+\sqrt{22}})-3\\
(-5)^2+2(-5)(\sqrt{22})+(\sqrt{22})^2\amp\wonder{=}-10(-5+\sqrt{22})-3\\
25-10\sqrt{22}+22 \amp\wonder{=}50-10\sqrt{22}-3\\
47-10\sqrt{22}\amp\confirm{=}47-10\sqrt{22}
\end{align*}
When the radicand from the quadratic formula, \(b^2-4ac\text{,}\) which is called the discriminant, is a negative number, the quadratic equation has no real solution. Example 7 shows what happens in this case.
Example 7.2.7.
Solve for \(y\) in \(y^2-4y+8=0\text{.}\)
Explanation.
Identify that \(\highlight{a=1}\text{,}\) \(\highlight{b=-4}\) and \(\highlight{c=8}\text{.}\) We will substitute them into the quadratic formula:
\begin{align*}
y\amp=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\\
\amp=\frac{-(\substitute{-4})\pm\sqrt{(\substitute{-4})^2-4(\substitute{1})(\substitute{8})}}{2(\substitute{1})}\\
\amp=\frac{4\pm\sqrt{16-32}}{2}\\
\amp=\frac{4\pm\sqrt{-16}}{2}
\end{align*}
The square root of a negative number is not a real number, so we will simply state that this equation has no real solutions.
Sometimes a radical equation gives rise to a quadratic equation, and the quadratic formula is useful.
Example 7.2.8.
Solve for \(z\) in \(\sqrt{z}+2=z\text{.}\)
Explanation.
We will isolate the radical first, and then square both sides.
\begin{align*}
\sqrt{z}+2\amp=z\\
\sqrt{z}\amp=z-2\\
\left(\sqrt{z}\right)^{\highlight{2}}\amp=(z-2)^{\highlight{2}}\\
z\amp=z^2-4z+4\\
0\amp=z^2-5z+4\\
z\amp=\frac{5\pm\sqrt{(-5)^2-4(1)(4)}}{2}\\
\amp=\frac{5\pm\sqrt{25-16}}{2}\\
\amp=\frac{5\pm\sqrt{9}}{2}\\
\amp=\frac{5\pm3}{2}
\end{align*}
\begin{align*}
z\amp=\frac{5-3}{2}\amp\text{ or }\amp\amp z\amp=\frac{5+3}{2}\\
z\amp=1\amp\text{ or }\amp\amp z\amp=4
\end{align*}
Because we squared both sides of an equation, we must check both solutions.
\begin{align*}
\sqrt{\substitute{1}}+2\amp\wonder{=}1\amp\sqrt{\substitute{4}}+2\amp\wonder{=}4\\
1+2\amp\reject{=}1\amp2+2\amp\confirm{=}4
\end{align*}
It turned out that \(1\) is an extraneous solution, but \(4\) is a valid solution. So the equation has one solution: \(4\text{.}\) The solution set is \(\{4\}\text{.}\)
Example 7.2.9.
Solve the equation \(\sqrt{2n-6}=1+\sqrt{n-2}\) for \(n\text{.}\)
Explanation.
We cannot isolate two radicals, so we will simply square both sides, and later try to isolate the remaining radical.
\begin{align*}
\sqrt{2n-6}\amp=1+\sqrt{n-2}\\
\left(\sqrt{2n-6}\right)^{\highlight{2}}\amp=\left(1+\sqrt{n-2}\right)^{\highlight{2}}\\
2n-6\amp=1^2+2\sqrt{n-2}+\left(\sqrt{n-2}\right)^2\\
2n-6\amp=1+2\sqrt{n-2}+n-2\\
2n-6\amp=2\sqrt{n-2}+n-1\\
n-5\amp=2\sqrt{n-2}\\
\end{align*}
Note here that we can leave the factor of \(2\) next to the radical. We will square the \(2\) also.
\begin{align*}
(n-5)^{\highlight{2}}\amp=\left(2\sqrt{n-2}\right)^{\highlight{2}}\\
n^2-10n+25\amp=4(n-2)\\
n^2-10n+25\amp=4n-8\\
n^2-14n+33\amp=0
\end{align*}
\begin{align*}
n\amp=\frac{14\pm\sqrt{14^2-4(1)(33)}}{2}\\
\amp=\frac{14\pm\sqrt{196-132}}{2}\\
\amp=\frac{14\pm\sqrt{64}}{2}\\
\amp=\frac{14\pm8}{2}
\end{align*}
\begin{align*}
n\amp=\frac{14-8}{2}\amp\text{ or }\amp\amp n\amp=\frac{14+8}{2}\\
n\amp=3\amp\text{ or }\amp\amp n\amp=11
\end{align*}
So our two potential solutions are \(3\) and \(11\text{.}\) We should now verify that they truly are solutions.
\begin{align*}
\sqrt{2(\substitute{3})-6}\amp\wonder{=}1+\sqrt{\substitute{3}-2}\amp\sqrt{2(\substitute{11})-6}\amp\wonder{=}1+\sqrt{\substitute{11}-2}\\
\sqrt{6-6}\amp\wonder{=}1+\sqrt{1}\amp\sqrt{22-6}\amp\wonder{=}1+\sqrt{9}\\
\sqrt{0}\amp\wonder{=}1+1\amp\sqrt{16}\amp\wonder{=}1+3\\
0\amp\reject{=}2\amp4\amp\confirm{=}4
\end{align*}
So, \(11\) is the only solution. The solution set is \(\{11\}\text{.}\)
Reading Questions 7.2.2 Reading Questions
1.
What is the formula for the discriminant? (The part of the quadratic formula inside the radical.)
2.
Are there any kinds of quadratic equations where the quadratic formula is not the best tool to use?
3.
Given a quadratic equation, will the quadratic formula always show you two real solutions?
Exercises 7.2.3 Exercises
Review and Warmup
Exercise Group.
Write each fraction in simplified form.
1.
- \(\displaystyle \frac{12}{40}\)
- \(\displaystyle \frac{-32}{-4}\)
- \(\displaystyle \frac{-40}{8}\)
- \(\displaystyle \frac{-14}{-24}\)
2.
- \(\displaystyle \frac{14}{20}\)
- \(\displaystyle \frac{40}{-8}\)
- \(\displaystyle \frac{-8}{2}\)
- \(\displaystyle \frac{-8}{-40}\)
3.
Write each fraction in simplified form.
- \(\displaystyle \frac{12}{20}\)
- \(\displaystyle \frac{-70}{30}\)
- \(\displaystyle \frac{-10}{-12}\)
- \(\displaystyle \frac{72}{28}\)
4.
Write each fraction in simplified form.
- \(\displaystyle \frac{-39}{30}\)
- \(\displaystyle \frac{-16}{-24}\)
- \(\displaystyle \frac{55}{40}\)
- \(\displaystyle \frac{33}{36}\)
Exercise Group.
Evaluate the given expression for the given values.
5.
\({b^{2}-4ac}\) for \(a=4\text{,}\) \(b=7\text{,}\) and \(c=1\)
6.
\({b^{2}-4ac}\) for \(a=5\text{,}\) \(b=9\text{,}\) and \(c=4\)
7.
\({b^{2}-4ac}\) for \(a=5\text{,}\) \(b=-7\text{,}\) and \(c=-2\)
8.
\({b^{2}-4ac}\) for \(a=-5\text{,}\) \(b=-5\text{,}\) and \(c=-4\)
Exercise Group.
Simplify the radical.
9.
\(\sqrt{48}\)
10.
\(\sqrt{45}\)
11.
\(\sqrt{24}\)
12.
\(\sqrt{90}\)
Skills Practice
Exercise Group.
Use the quadratic formula to solve the equation.
13.
\({x^{2}-3x-18}=0\)
14.
\({x^{2}+16x+63}=0\)
15.
\({2x^{2}-5x+2}=0\)
16.
\({4x^{2}+19x-63}=0\)
17.
\({27x^{2}+15x-8}=0\)
18.
\({21x^{2}-17x+2}=0\)
19.
\({x^{2}-x+3}=0\)
20.
\({x^{2}+3x+4}=0\)
21.
\({x^{2}+{\frac{20}{3}}x - {\frac{7}{3}}}=0\)
22.
\({x^{2} - {\frac{11}{3}}x+2}=0\)
23.
\({x^{2}-8x+16}=0\)
24.
\({x^{2}-12x+36}=0\)
25.
\({x^{2}-7x+2}=0\)
26.
\({x^{2}+3x+8}=0\)
27.
\({x^{2}+{\frac{2}{5}}x - {\frac{24}{25}}}=0\)
28.
\({x^{2}+{\frac{11}{3}}x+{\frac{28}{9}}}=0\)
29.
\({x^{2}+8x+4}=0\)
30.
\({x^{2}+7x+5}=0\)
31.
\({x^{2}+x+{\frac{1}{4}}}=0\)
32.
\({x^{2} - {\frac{8}{7}}x+{\frac{16}{49}}}=0\)
33.
\({x^{2}-6x+6}=0\)
34.
\({x^{2}+5x+1}=0\)
35.
\({-5x^{2}+10x-3}=0\)
36.
\({-6x^{2}+14x-3}=0\)
37.
\({81x^{2}+72x+16}=0\)
38.
\({49x^{2}+28x+4}=0\)
39.
\({x^{2}+x - {\frac{2}{3}}}=0\)
40.
\({x^{2}-3x+{\frac{5}{3}}}=0\)
41.
\({{\frac{1}{3}}x^{2} - {\frac{4}{3}}x+{\frac{1}{2}}}=0\)
42.
\({{\frac{1}{3}}x^{2}+{\frac{1}{2}}x - {\frac{1}{2}}}=0\)
43.
\({x^{2}-17.6x+77.44}=0\)
44.
\({x^{2}+15.8x+62.41}=0\)
45.
\({-5.6x^{2}-72.8x-236.6}=0\)
46.
\({2.4x^{2}+15.84x+26.136}=0\)
47.
\({x^{2}+9.2x+14.4}=0\)
48.
\({x^{2}+3.6x-14.4}=0\)
49.
\({x^{2}-9.4x+2.6}=0\)
50.
\({x^{2}+4.2x+3.6}=0\)
51.
\({5.3x^{2}-11.2x+4.6}=0\)
52.
\({8.5x^{2}-6.8x-6.9}=0\)
53.
\({x^{2}+4x}={5}\)
54.
\({x^{2}-3x}={-2}\)
55.
\({x^{2}}={4x+21}\)
56.
\({x^{2}}={-x+20}\)
57.
\({2x^{2}+49}={-21x}\)
58.
\({7x^{2}+6}={23x}\)
59.
\({3x^{2}}={-31x-36}\)
60.
\({2x^{2}}={x+6}\)
61.
\({7x^{2}+32}={36x}\)
62.
\({32x^{2}+27}={-84x}\)
63.
\({45x^{2}}={x+28}\)
64.
\({9x^{2}}={-27x-14}\)
65.
\({x^{2}+4}={-x}\)
66.
\({x^{2}+5}={-3x}\)
67.
\({x^{2}+{\frac{5}{3}}x}={ + {\frac{2}{3}}}\)
68.
\({x^{2} - {\frac{22}{3}}x}={-8}\)
69.
\({x^{2} - {\frac{15}{32}}}={ + {\frac{1}{8}}x}\)
70.
\({x^{2}+{\frac{2}{3}}}={ + {\frac{11}{6}}x}\)
71.
\({x^{2}-6x}={9}\)
72.
\({x^{2}+9}={-9x}\)
73.
\({4x^{2}+5}={-7x}\)
74.
\({5x^{2}+2}={2x}\)
75.
\({x^{2}}={-{\frac{37}{7}}x + {\frac{30}{7}}}\)
76.
\({x^{2}}={-{\frac{33}{5}}x + {\frac{14}{5}}}\)
77.
\({x^{2}}={ + {\frac{8}{3}}x-{\frac{5}{12}}}\)
78.
\({x^{2}}={ + {\frac{87}{28}}x-{\frac{27}{14}}}\)
79.
\({-8x^{2}+7}={9x}\)
80.
\({-9x^{2}-8}={-20x}\)
81.
\({x^{2}}={-4x+7}\)
82.
\({x^{2}}={3x+5}\)
83.
\({-3x^{2}}={-11x+9}\)
84.
\({6x^{2}}={-16x-5}\)
Radical Equations That Give Rise to Quadratic Equations.
Solve the equation.
85.
\({5\sqrt{x}}={x+6}\)
86.
\({6\sqrt{x}}={x+8}\)
87.
\({2\sqrt{x}}={8-x}\)
88.
\({\sqrt{x}}={x-12}\)
89.
\({3\sqrt{x}}={x+8}\)
90.
\({3\sqrt{x}}={x+8}\)
91.
\({4\sqrt{x}}={-x-3}\)
92.
\({5\sqrt{x}}={-x-4}\)
93.
\({\sqrt{5x+11}}={x+3}\)
94.
\({\sqrt{5x-1}}={x+1}\)
95.
\({6\sqrt{5x+2}-5x}={10}\)
96.
\({6\sqrt{5x+5}-13}={5x}\)
97.
\({\sqrt{2x+6}+2x}={6}\)
98.
\({\sqrt{2x-1}+2x}={3}\)
Applications
99.
While standing on a rooftop that is 5 m high off the ground, you throw a tennis ball off the roof in an arc. Because of the speed that you throw the ball, its height from the ground, in meters, \(t\) seconds after the throw is \({-4.9t^{2}+17t+7}\text{.}\) How long will it be until the ball hits the ground?
100.
While standing on a tree branch that is 22 ft high off the ground, a squirrel kicks a nut in an arc. The nut falls cleanly to the ground without hitting anything on the way down. While the nut is in the air, its height from the ground, in feet, \(t\) seconds after the kick is \({-16t^{2}+1.7t+22}\text{.}\) How long will it be until the nut hits the ground?
101.
An astronaut on the moon makes a running jump off a cliff onto a broad flat plain. The clifftop is 4 m higher than the plain. Because of the slight upward jump, the astronaut’s height from the plain, in meters, \(t\) seconds after the jump is \({-0.81t^{2}+1.8t+6}\text{.}\) How long will it be until the astronaut lands in the plain?
102.
An robot on Mars makes a running jump off a cliff onto a broad flat plain. The clifftop is 15 m higher than the plain. Because of the slight upward jump, the robot’s height from the plain, in meters, \(t\) seconds after the jump is \({-1.85t^{2}+2.8t+17}\text{.}\) How long will it be until the robot lands in the plain?
103.
One rectangular wall in your classroom is \({5.75\ {\rm ft}}\) longer than it is tall. The total area of the wall is \({164\ {\rm ft^{2}}}\text{.}\) How tall is the wall?
104.
The rectangular floor of your classroom is \({17.25\ {\rm m}}\) longer than it is wide. The total floor area is \({301\ {\rm m^{2}}}\text{.}\) How wide is the floor? (This is asking for the shorter dimension.)
105.
A metals factory will produce steel picture frames in the form of a rectagle with a smaller rectangle cut out, as in the diagram. The widths of the four edges is to be consistent, and leave a \({88\ {\rm cm}}\) by \({55\ {\rm cm}}\) visible area for photos and other images. There is a standard thickness for the metal from which these frames will be cut, and the manufacturer has a target weight in mind for the final product so that shipping costs will be kept low. This leads to the decision that the surface area of the frame needs to be \({987\ {\rm cm^{2}}}\text{.}\) How wide should the four edges be? (What is the value of \(x\) in the diagram?)
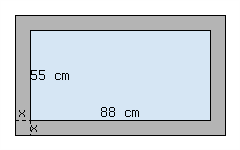
106.
A vegetable garden will be surrounded by a frame of grass sod. The garden itself will be \({19\ {\rm ft}}\) by \({8\ {\rm ft}}\text{.}\) The widths of the four edges of the frame will be equal to each other. There is only \({167\ {\rm ft^{2}}}\) of grass sod available, and it will all be used for this frame. How wide should the four edges be? (What is the value of \(x\) in the diagram?)
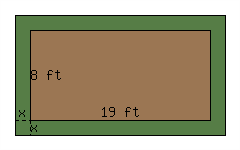
107.
You are ready to self-publish a book online. It has cost you \({\$20{,}000}\) to get to this point, including hours of labor and printing equipment. To actually print and mail one copy costs you \({\$8.50}\text{.}\) If the book were free, you estimate \(50000\) would order a copy. If you increase the price to \(p\) dollars per book you will have fewer orders, and after studying similar book sales you estimate you would have \({50000-1000p}\) sales. What is the largest price that you could set to end up with a profit of \({\$40{,}000}\text{?}\)
108.
A new electric car company is ready to sell its debut model. It has cost the company \({\$300}\) million to set up a production line and be ready to produce cars. To actually build and deliver one of the new models costs \({\$40}\) thousand. Studying the current state of the electric car market, you estimate that if you charge each customer \(p\) dollars, you would have \({1000000-4p}\) sales. What is the lowest price that you could set to end up with a profit of \({\$1}\) billion?
109.
If you add \({{\frac{4}{3}}}\) to a certain positive number, then also subtract \(2\) from that same number, and multiply the results, you get \({{\frac{13}{3}}}\text{.}\) What was the original number?
110.
If you double a certain positive number, then also add \({{\frac{5}{2}}}\) to that same number, and multiply the results, you get \({12}\text{.}\) What was the original number?
Challenge
111.
Solve for \(x\) in the equation \(mx^{2}+nx+p=0\text{,}\) assuming \(m\neq0\text{.}\)
You have attempted of activities on this page.

