Example 8.4.2.
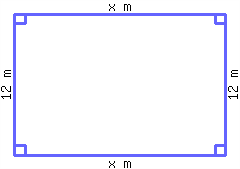
An Olympic-size swimming pool is rectangular and 50 m in length. We don’t know its width, but we do know that it required 150 m of painter’s tape to outline the edge of the pool during recent renovations. Use this information to set up an equation and find the width of the pool.
Explanation.
The pool’s shape is a rectangle, so it helps to sketch a rectangle representing the pool as in Figure 3. Since we know its length is 50 m, it is a good idea to label that in the sketch. The width is our unknown quantity, so we can use \(w\) as a variable to represent the pool’s width in meters and label that too.
Since it required 150 m of painter’s tape to outline the pool, we know the perimeter of the pool is 150 m. This suggests using the perimeter formula for a rectangle: \(P=2(\ell+w)\text{.}\) (This formula was discussed in Subsection 8.3.1).
With this formula, we can substitute \(150\) in for \(P\) and \(50\) in for \(\ell\text{:}\)
\begin{equation*}
150=2(50+w).
\end{equation*}
Now we can solve the equation for the width of the pool.
First, we will distribute on the right side, and then isolate \(w\text{.}\)
\begin{align*}
150\amp=100+2w\\
150\subtractright{100}\amp=100\subtractright{100}+2w\\
50\amp=2w\\
\divideunder{50}{2}\amp=\divideunder{2w}{2}\\
25\amp=w\text{.}
\end{align*}
Checking the solution \(w=25\) meters:
\begin{align*}
150\amp=2(50+w)\\
150\amp\wonder{=}2(50+\substitute{25})\\
150\amp\wonder{=}2(75)\\
150\amp\confirm{=}150\text{.}
\end{align*}
We found that the width of the pool is \(25\) meters.