ORCCA Geometry Formulas

Section 8.3 Geometry Formulas

Objectives: PCC Course Content and Outcome Guide

In this section we will evaluate some formulas related to the geometry of two- and three-dimensional shapes.

Figure 8.3.1. Alternative Video Lesson

Subsection 8.3.1 Evaluating Perimeter and Area Formulas

Rectangles.

The rectangle in Figure 2 has a length (as measured by the edges on the top and bottom) and a width (as measured by the edges on the left and right).

Figure 8.3.2. A Rectangle

Perimeter is the distance around the edge(s) of a two-dimensional shape. To calculate perimeter, start from a point on the shape (usually a corner), travel around the shape, and add up the total distance traveled. For the rectangle in Figure 2, if we travel around it, the total distance would be:

\begin{aligned} rectangle perimeter & = 3 cm + 2 cm + 3 cm + 2 cm \\ = 10 cm . \end{aligned}

Another way to compute a rectangle’s perimeter would be to start at one corner, add up the edge length half-way around, and then double that. So we could have calculated the perimeter this way:

\begin{aligned} rectangle perimeter & = 2 (3 cm + 2 cm) \\ = 2 (5 cm) \\ = 10 cm . \end{aligned}

There is nothing special about this rectangle having length 3 cm and width 2 cm. With a generic rectangle, it has some length we can represent with the variable

ℓ

and some width we can represent with the variable

w .

We can use

P

to represent its perimeter, and then the perimeter of the rectangle will be given by:

P = 2 (ℓ + w) .

Area is the number of

1 \times 1

squares that fit inside a two-dimensional shape (possibly after morphing them into non-square shapes). If the edges of the squares are, say, 1 cm long, then the area is measured in “square cm,” written cm². In Figure 2, the rectangle has six 1 cm × 1 cm squares, so its area is

6

square centimeters.

Note that we can find that area by multiplying the length and the width:

\begin{aligned} rectangle area & = (3 cm) \cdot (2 cm) \\ = 6 {cm}^{2} \end{aligned}

Again, there is nothing special about this rectangle having length 3 cm and width 2 cm. With a generic rectangle, it has some length we can represent with the variable

ℓ

and some width we can represent with the variable

w .

We can represent its area with the variable

A,

and then the area of the rectangle will be given by:

A = ℓ \cdot w .

Checkpoint 8.3.3.

Find the perimeter and area of the rectangle.

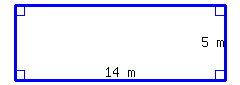
Its perimeter is and its area is .

Explanation.

Using the perimeter and area formulas for a rectangle, we have:

\begin{aligned} P & = 2 (ℓ + w) & A & = ℓ \cdot w \\ = 2 (14 + 5) & = 14 \cdot 5 \\ = 2 (19) & = 70 \\ = 38 \end{aligned}

Since length and width were measured in meters, we find that the perimeter is

38

meters and the area is

70

square meters.

Example 8.3.4.

Imagine a rectangle with width 7.5 in and height 11.43 cm as in Figure 5.

Find the perimeter (in inches) of the rectangle.
Find the area (in square centimeters) of the rectangle.

Figure 8.3.5. A Rectangle

Explanation.

To find the perimeter (in inches) of the rectangle, we should first convert all lengths into inches. By Appendix A, we know that $1 in = 2.54 cm .$ So, we have

$\begin{aligned} 11.43 cm & = \frac{11.43 cm}{1} \cdot \frac{1 in}{2.54 cm} \\ = \frac{11.43}{2.54} in \\ = 4.5 in \end{aligned}$

So, the total perimeter is $2 \cdot 4.5 in + 2 \cdot 7.5 in = 24 in .$
To find the area (in square centimeters) of the rectangle, we should first convert all lengths into centimeters. So, we have

$\begin{aligned} 7.5 in & = \frac{7.5 in}{1} \cdot \frac{2.54 cm}{1 in} \\ = \frac{7.5}{2.54} cm \\ = 19.05 cm \end{aligned}$

So, the total area is $19.05 cm \cdot 11.43 cm = 217.7415 {cm}^{2} .$

Triangles.

The perimeter of a general triangle has no special formula—all that is needed is to add the lengths of its three sides. The area of a triangle is a bit more interesting. In Figure 6, there are three triangles. From left to right, there is an acute triangle, a right triangle, and an obtuse triangle. Each triangle is drawn so that there is a “bottom” horizontal edge. This edge is referred to as the “base” of the triangle. With each triangle, a “height” that is perpendicular to the base is also illustrated.

Figure 8.3.6. Triangles

Figure 8.3.7. Triangles

Each of these triangles has the same base width, 3 cm, and the same height, 2 cm. Note that they each have the same area as well. Figure 7 illustrates how they each have an area of 3 cm².

As with the triangles in Figure 7, you can always rearrange little pieces of a triangle so that the resulting shape is a rectangle with the same base width, but with a height that’s one-half of the triangle’s height. With a generic rectangle, it has some base width we can represent with the variable

b

and some height we can represent with the variable

h .

We can represent its area with the variable

A,

and then the area of the triangle will be given by

A = b \cdot (\frac{1}{2} h),

or more conventionally:

A = \frac{1}{2} b h .

Checkpoint 8.3.8.

Find the perimeter and area of the triangle.

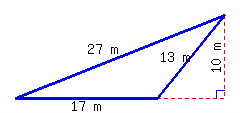
Its perimeter is and its area is .

Explanation.

For perimeter, we just add the three side lengths:

\begin{aligned} P & = 13 + 27 + 17 \\ = 57 \end{aligned}

For area, we use the triangle area formula:

\begin{aligned} A & = \frac{1}{2} b h \\ = \frac{1}{2} (17) (10) \\ = 5 (17) \\ = 85 \end{aligned}

Since length and width were measured in meters, we find that the perimeter is

57

meters and the area is

85

square meters.

Circles.

To find formulas for the perimeter and area of a circle, it helps to first know that there is a special number called

π

(spelled “pi” and pronounced like “pie”) that appears in many places in mathematics. The decimal value of

π

is about

3.14159265 \dots,

and it helps to memorize some of these digits. It also helps to understand that

π

is a little larger than

3 .

There are many definitions for

π

that can explain where it comes from and how you can find all its decimal places, but here we are just going to accept that it is a special number, and it is roughly

3.14159265 \dots .

The perimeter of a circle is the distance around its edge. For circles, the perimeter has a special name: the circumference. Imagine wrapping a string around the circle and cutting it so that it makes one complete loop. If we straighten out that piece of string, we have a length that is just as long as the circle’s circumference.

Figure 8.3.9. Circumference and Diameter

As we can see in Figure 9, the circumference of a circle is a little more than three times as long as its diameter. (The diameter of a circle is the length of a straight line running from a point on the edge through the center to the opposite edge.) In fact, the circumference is actually exactly

π

times the length of the diameter. With a generic circle, it has some diameter we can represent with the variable

d .

We can represent its circumference with the variable

c,

and then the circumference of the circle will be given by:

c = π d .

Alternatively, we often prefer to work with a circle’s radius instead of its diameter. The radius is the distance from any point on the circle’s edge to its center. (Note that the radius is half the diameter.) From this perspective, we can see in Figure 10 that the circumference is a little more than

6

times the radius.

Figure 8.3.10. Circumference and Radius

This gives us another formula for a circle’s circumerence that uses the variable

r

for its radius:

c = π \cdot 2 r .

Or more conventionally,

c = 2 π r .

There is also a formula for the area of a circle based on its radius. Figure 11 shows how three squares can be cut up and rearranged to fit inside a circle. This shows how the area of a circle of radius

r

is just a little larger than

3 r^{2} .

Since

π

is just a little larger than

3,

could it be that the area of a circle is given by

π r^{2} ?

Figure 8.3.11. Circle area is slightly larger than

3 r^{2} .

One way to establish this formula is to imagine slicing up the circle into many pie slices as in Figure 12. Then you can rearrange the slices into a strange shape that is almost a rectangle with height equal to the radius of the original circle, and width equal to half the circumference of the original circle.

Figure 8.3.12. Reasoning the circle area formula.

Since the area of the circle is equal to the area of the almost-rectangular shape in Figure 12, we have the circle area formula:

A = π r^{2} .

Checkpoint 8.3.13.

A circle’s diameter is

6 m .

This circle’s circumference, in terms of $π,$ is .
This circle’s circumference, rounded to the hundredth place, is .
This circle’s area, in terms of $π,$ is .
This circle’s area, rounded to the hundredth place, is .

Explanation.

We use

r

to represent radius and

d

to represent diameter. In this problem, it’s given that the diameter is

6 m .

A circle’s radius is half as long as its diameter, so the radius is

3 m .

Throughout these computations, all quantities have units attached, but we only show them in the final step.

$\begin{aligned} c & = π d \\ = π \cdot 6 \\ = 6 π m \end{aligned}$
$\begin{aligned} c & = π d \\ \approx 3.1415926 \cdot 6 \\ \approx 18.85 m \end{aligned}$
$\begin{aligned} A & = π r^{2} \\ = π \cdot 3^{2} \\ = π \cdot 9 \\ = 9 π m^{2} \end{aligned}$
$\begin{aligned} A & = π r^{2} \\ \approx 3.1415926 \cdot 3^{2} \\ \approx 3.1415926 \cdot 9 \\ \approx 28.27 m^{2} \end{aligned}$

Subsection 8.3.2 Volume

The volume of a three-dimensional object is the number of

1 \times 1 \times 1

cubes that fit inside the object (possibly after morphing them into non-cube shapes). If the edges of the cubes are, say, 1 cm long, then the volume is measured in “cubic centimeters ,” written cm³.

Rectangular Prisms.

The 3D shape in Figure 14 is called a rectangular prism.

a rectangular box made of 1 inch cubes; it is 5 inches wide, 4 inches deep and 3 inches high — Figure 8.3.14. Volume of a Rectangular Prism

The rectangular prism in Figure 14 is composed of

1 in \times 1 in \times 1 in

unit cubes, with each cube’s volume being

1

cubic inch (or

{in}^{3}

). The shape’s volume is the number of such unit cubes. The bottom face has

5 \cdot 4 = 20

unit squares. Since there are

3

layers of cubes, the shape has a total of

3 \cdot 20 = 60

unit cubes. In other words, the shape’s volume is 60 in³ because it has sixty 1 in × 1 in × 1 in cubes inside it.

We found the number of unit squares in the bottom face by multiplying

5 \cdot 4 = 20 .

Then to find the volume, we multiplied by

3

because there are three layers of cubes. So one formula for a prism’s volume is

V = w d h

where

V

stands for volume,

w

for width,

d

for depth, and

h

for height.

Checkpoint 8.3.15.

A masonry brick is in the shape of a rectangular prism and is

8

inches wide,

3.5

inches deep, and

2.25

inches high. What is its volume?

Explanation.

Using the formula for the volume of a rectangular prism:

\begin{aligned} V & = w d h \\ = 8 (3.5) (2.25) \\ = 63 \end{aligned}

So the brick’s volume is

63

cubic inches.

Example 8.3.16.

Imagine a rectangular prism with width 40 in, depth 4 ft, and height 2 yd as in Figure 17.

Find the volume (in cubic feet) of the prism.
Find the surface area (in square inches) of the prism.

a rectangular box; it is 40 inches wide, 4 feet deep, and 2 yards high — Figure 8.3.17. A Prism

Explanation.

To find the volume (in cubic feet) of the prism, we should first convert all lengths into feet. By Appendix A, we know that $1 ft = 12 in$ and that $1 yd = 3 ft .$ So, we have

$\begin{aligned} 40 in & = \frac{40 in}{1} \cdot \frac{1 ft}{12 in} \\ = \frac{40}{12} ft \\ = \frac{10}{3} ft \end{aligned}$

and

$\begin{aligned} 2 yd & = \frac{2 yd}{1} \cdot \frac{3 ft}{1 yd} \\ = 2 \cdot 3 ft \\ = 6 ft \end{aligned}$

So, the total volume is $4 ft \cdot \frac{10}{3} ft \cdot 6 ft = 80 {ft}^{3} .$
To find the surface area (in square inches) of the prism, we should first convert all lengths into inches. So, we have

$\begin{aligned} 4 ft & = \frac{4 ft}{1} \cdot \frac{12 in}{1 ft} \\ = 4 \cdot 12 in \\ = 48 in \end{aligned}$

and

$\begin{aligned} 2 yd & = \frac{2 yd}{1} \cdot \frac{36 in}{1 yd} \\ = 2 \cdot 36 in \\ = 72 in \end{aligned}$

To find the surface area, we should add up the six areas of the faces of the prism, each of which is a rectangle. Note that each face has a corresponding symmetrical face on the other side of the prism.

$\begin{aligned} Surface Area & = \overset{top and bottom}{\overset{⏞}{2 (40 in \overset{}{\cdot} 36 in)}} + \overset{left and right}{\overset{⏞}{2 (48 in \overset{}{\cdot} 36 in)}} + \overset{front and back}{\overset{⏞}{2 (40 in \overset{}{\cdot} 48 in)}} \\ = 10176 {in}^{2} \end{aligned}$

Cylinders.

A cylinder is not a prism, but it has some similarities. Instead of a square base, the base is a circle. Its volume can also be calculated in a similar way to how prism volume is calculated. Let’s look at an example.

Example 8.3.18.

Find the volume of a cylinder with a radius of

3

meters and a height of

2

meters.

Explanation.

The base of the cylinder is a circle. We know the area of a circle is given by the formula

A = π r^{2},

so the base area is 9

π

m², or about 28.27 m². That means about

28.27

unit squares can fit into the base. One of them is drawn in Figure 20 along with two unit cubes above it.

the same cylinder with two unit cubes inside highlighted — Figure 8.3.20. Finding Cylinder Volume

For each unit square in the base circle, there are two unit cubes of volume. So the volume is the base area times the height:

9 π m^{2} \cdot 2 m,

which equals

18 π m^{3} .

Approximating

π

with a decimal value, this is about 56.55 m³.

Example 18 demonstrates that the volume of a cylinder can be calculated with the formula

V = π r^{2} h

where

r

is the radius and

h

is the height.

Checkpoint 8.3.21.

A soda can is basically in the shape of a cylinder with radius

1.3

inches and height

4.8

inches. What is its volume?

Its exact volume in terms of

π

is: .

As a decimal approximation rounded to four significant digits, its volume is: .

Explanation.

Using the formula for the volume of a cylinder:

\begin{aligned} V & = π r^{2} h \\ = π (1.3)^{2} (4.8) \\ = 8.112 π \\ \approx 25.48 \end{aligned}

So the can’s volume is

8.112 π

cubic inches, which is about

25.48

cubic inches.

Note that the volume formulas for a rectangular prism and a cylinder have something in common: both formulas first find the area of the base (which is a rectangle for a prism and a circle for a cylinder) and then multiply by the height. So there is another formula

V = B h

that works for both shapes. Here,

B

stands for the base area (which is

w d

for a prism and

π r^{2}

for a cylinder.)

Subsection 8.3.3 Summary

Here is a list of all the formulas we’ve learned in this section.

List 8.3.22. Geometry Formulas

Perimeter of a Rectangle: $P = 2 (ℓ + w)$
Area of a Rectangle: $A = ℓ w$
Area of a Triangle: $A = \frac{1}{2} b h$
Circumference of a Circle: $c = 2 π r$
Area of a Circle: $A = π r^{2}$
Volume of a Rectangular Prism: $V = w d h$
Volume of a Cylinder: $V = π r^{2} h$
Volume of a Rectangular Prism or Cylinder: $V = B h$

Exercises 8.3.4 Exercises

Perimeter and Area.

1.

Find the perimeter and area of the rectangle.

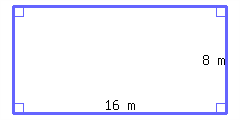
Its perimeter is and its area is .

2.

Find the perimeter and area of the rectangle.

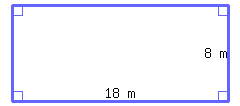
Its perimeter is and its area is .

Exercise Group.

3.

Find the perimeter of the rectangle below.

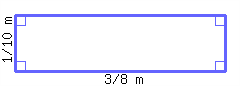
4.

Find the perimeter of the rectangle below.

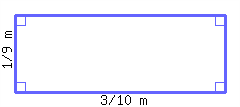
5.

Find the area of the rectangle below.

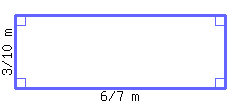
6.

Find the area of the rectangle below.

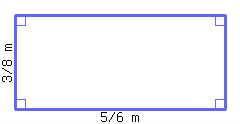
7.

Find the perimeter and area of a rectangular table top with a length of

5.2 f t

and a width of

34 i n .

Its perimeter is and its area is .

8.

Find the perimeter and area of a rectangular table top with a length of

5.4 f t

and a width of

30 i n .

Its perimeter is and its area is .

9.

Find the perimeter and area of the square.

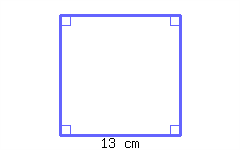
The perimeter is .
The area is .

10.

Find the perimeter and area of the square.

The perimeter is .
The area is .

11.

Find the perimeter and area of the triangle.

Its perimeter is and its area is .

12.

Find the perimeter and area of the triangle.

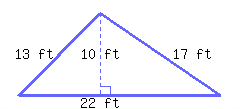
Its perimeter is and its area is .

13.

Find the perimeter and area of the right triangle.

Its perimeter is and its area is .

14.

Find the perimeter and area of the right triangle.

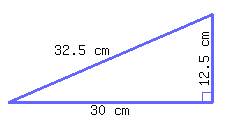
Its perimeter is and its area is .

15.

Find the perimeter and area of the triangle.

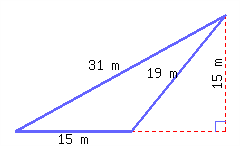
Its perimeter is and its area is .

16.

Find the perimeter and area of the triangle.

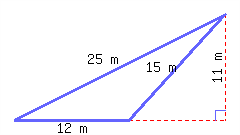
Its perimeter is and its area is .

17.

The area of the triangle below is square feet.

18.

The area of the triangle below is square feet.

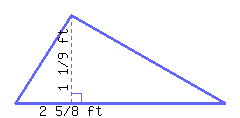
19.

Find the area of a triangular flag with a base of

3.9 m

and a height of

120 c m .

Its area is .

20.

Find the area of a triangular flag with a base of

2 m

and a height of

80 c m .

Its area is .

21.

Find the perimeter and area of this polygon.

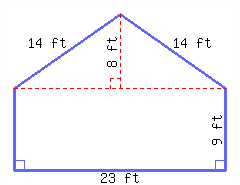
Its perimeter is and its area is .

22.

Find the perimeter and area of this polygon.

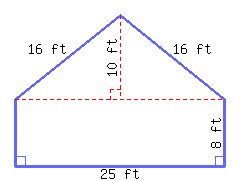
Its perimeter is and its area is .

23.

Find the perimeter and area of this shape.

Its perimeter is and its area is .

24.

Find the perimeter and area of this shape.

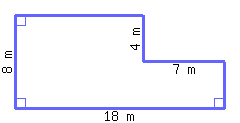
Its perimeter is and its area is .

25.

Find the perimeter and area of this polygon.

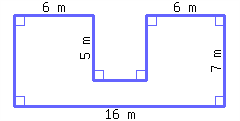
Its perimeter is and its area is .

26.

Find the perimeter and area of this polygon.

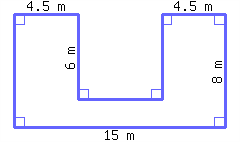
Its perimeter is and its area is .

Exercise Group.

27.

A trapezoid’s area can be calculated by the formula

A = \frac{1}{2} (b_{1} + b_{2}) h,

where

A

stands for area,

b_{1}

for the first base’s length,

b_{2}

for the second base’s length, and

h

for height.

Find the area of the trapezoid below.

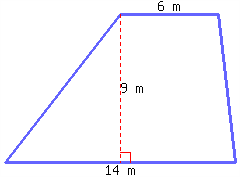
28.

A trapezoid’s area can be calculated by the formula

A = \frac{1}{2} (b_{1} + b_{2}) h,

where

A

stands for area,

b_{1}

for the first base’s length,

b_{2}

for the second base’s length, and

h

for height.

Find the area of the trapezoid below.

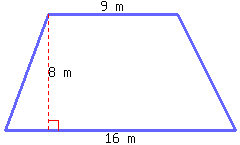
Exercise Group.

29.

The formula

A = \frac{1}{2} r n s

gives the area of a regular polygon with side length

s,

number of sides

n

and, apothem

r .

(The apothem is the distance from the center of the polygon to one of its sides.)

What is the area of a regular pentagon with

s = 3 i n

and

r = 56 i n ?

30.

The formula

A = \frac{1}{2} r n s

gives the area of a regular polygon with side length

s,

number of sides

n

and, apothem

r .

(The apothem is the distance from the center of the polygon to one of its sides.)

What is the area of a regular

96

-gon with

s = 15 i n

and

r = 84 i n ?

Exercise Group.

31.

A circle’s radius is

4 m .

The circumference, in terms of $π,$ is .
This circle’s circumference, rounded to the hundredths place, is .
This circle’s area, in terms of $π,$ is .
This circle’s area, rounded to the hundredths place, is .

32.

A circle’s radius is

5 m .

The circumference, in terms of $π,$ is .
This circle’s circumference, rounded to the hundredths place, is .
This circle’s area, in terms of $π,$ is .
This circle’s area, rounded to the hundredths place, is .

33.

A circle’s diameter is

12 m .

This circle’s circumference, in terms of $π,$ is .
This circle’s circumference, rounded to the hundredths place, is .
This circle’s area, in terms of $π,$ is .
This circle’s area, rounded to the hundredths place, is .

34.

A circle’s diameter is

14 m .

This circle’s circumference, in terms of $π,$ is .
This circle’s circumference, rounded to the hundredths place, is .
This circle’s area, in terms of $π,$ is .
This circle’s area, rounded to the hundredths place, is .

Exercise Group.

35.

Find the perimeter and area of this shape, which is a semicircle on top of a rectangle.

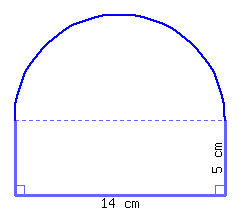
Its perimeter is and its area is .

36.

Find the perimeter and area of this shape, which is a semicircle on top of a rectangle.

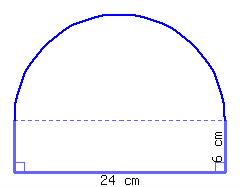
Its perimeter is and its area is .

Volume.

37.

Find the volume of this rectangular prism.

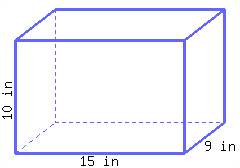
38.

Find the volume of this rectangular prism.

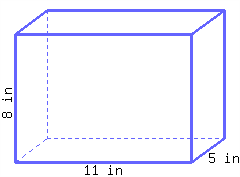
39.

Find the volume of this rectangular prism.

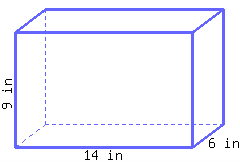
40.

Find the volume of this rectangular prism.

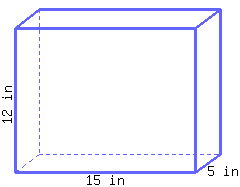
41.

A cube’s side length is

5 c m .

Its volume is .

42.

A cube’s side length is

6 c m .

Its volume is .

43.

Find the volume of this cylinder.

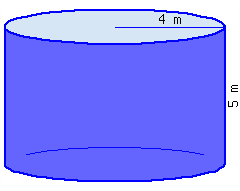
This cylinder’s volume, in terms of $π,$ is .
This cylinder’s volume, rounded to the hundredths place, is .

44.

Find the volume of this cylinder.

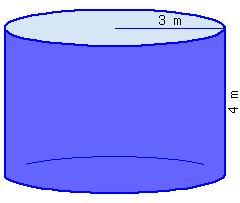
This cylinder’s volume, in terms of $π,$ is .
This cylinder’s volume, rounded to the hundredths place, is .

45.

Find the volume of this cylinder.

This cylinder’s volume, in terms of $π,$ is .
This cylinder’s volume, rounded to the hundredths place, is .

46.

Find the volume of this cylinder.

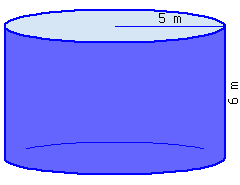
This cylinder’s volume, in terms of $π,$ is .
This cylinder’s volume, rounded to the hundredths place, is .

47.

A cylinder’s base’s diameter is

20 f t,

and its height is

2 f t .

This cylinder’s volume, in terms of $π,$ is .
This cylinder’s volume, rounded to the hundredths place, is .

48.

A cylinder’s base’s diameter is

14 f t,

and its height is

3 f t .

This cylinder’s volume, in terms of $π,$ is .
This cylinder’s volume, rounded to the hundredths place, is .

Exercise Group.

49.

The formula

V = \frac{1}{3} \cdot s^{2} \cdot h

gives the volume of a right square pyramid.

What is the volume of a right square pyramid with

s = 27 i n

and

h = 24 i n ?

50.

The formula

V = \frac{1}{3} \cdot s^{2} \cdot h

gives the volume of a right square pyramid.

What is the volume of a right square pyramid with

s = 36 i n

and

h = 88 i n ?

51.

Fill out the table with various formulas as they were given in this section.

Rectangle Perimeter
Rectangle Area
Triangle Area
Circle Circumference
Circle Area
Rectangular Prism Volume
Cylinder Volume
Volume of either Rectangular Prism or Cylinder

You have attempted 1 of 2 activities on this page.

Prev Top Next