Section 13.1 Overview of Graphing
In this section, we will review how to graph lines and general functions which will be useful when we graph parabolas in the next section.
Subsection 13.1.1 Graphing Lines by Plotting Points
Sometimes, the easiest way to make a graph of an equation is by making a table and plotting points. (This was the approach in Section 3.2.) Let’s refresh ourselves on how this works.
Example 13.1.2.
A bathtub is holding \(12\) gallons of water. The drain starts to leak water at a constant rate of \(0.6\) gallons per second. A linear function with formula \(W(x)=-0.6x+12\) can be used to model the amount of water, in gallons, in the tub \(x\) seconds after it started draining. Let’s make a graph of this function. The most straightforward method to graph any function is to build a table of \(x\)- and \(y\)-values, and then plot the points.
| \(x\) | \(W(x)=-0.6x+12\) | Point | Interpretation |
| \(0\) |
\(-0.6(0)+12\) \({}=12\) |
\((0,12)\) | There were \(12\) gallons of water in the tub when the tub started to drain. |
| \(1\) |
\(-0.6(1)+12\) \({}=11.4\) |
\((1,11.4)\) | There were \(11.4\) gallons in the tub \(1\) second after the tub started to drain. |
| \(2\) |
\(-0.6(2)+12\) \({}=10.8\) |
\((2,10.8)\) | There were \(10.8\) gallons in the tub \(2\) seconds after the tub started to drain. |
| \(3\) |
\(-0.6(3)+12\) \({}=10.2\) |
\((3,10.2)\) | There were \(10.2\) gallons in the tub \(3\) seconds after the tub started to drain. |
| \(4\) |
\(-0.6(4)+12\) \({}=9.6\) |
\((4,9.6)\) | There were \(9.6\) gallons in the tub \(4\) seconds after the tub started to drain. |
Could we have made a more helpful table? Maybe. The \(y\)-values are close together and for the most part they are decimals which can be difficult to plot accurately. No matter, for now we use these points and make a plot.
The advantage of plotting points is that it is a universal method to graph any function. It is easy to forget about this method after learning faster ways to graph functions, so to keep this method in your mathematical tool box in case you come across something that you don’t know or remember how to graph.
Checkpoint 13.1.5.
Make a table for the equation.
| \(x\) | \(y={\frac{8}{5}}x - 9\) |
| Values of \(x\) and \(y\) satisfying the equation \(y={\frac{8}{5}}x - 9\) |
Explanation.
Since this equation has a fractional coefficient for \(x\) with denominator \(5\text{,}\) it would be wise to choose our own \(x\)-values that are multiples of \(5\text{.}\) Then when we use them to solve for \(y\text{,}\) the denominator will be cleared, and we will not need to continue with fraction arithmetic.
This solution will use the \(x\)-values \(-5\text{,}\) \(0\text{,}\) \(5\text{,}\) \(10\) and \(15\text{.}\) The choice to use these \(x\)-values is arbitrary, but they are small multiples of \(5\text{,}\) which will make computation easier.
One at a time, we substitute these \(x\)-values into the equation \(y={\frac{8}{5}}x - 9\text{,}\) and solve for \(y\text{:}\)
\begin{equation*}
\begin{aligned}
y = {\frac{8}{5}}\left( -5 \right) - 9 \amp \implies y=-17\\
y = {\frac{8}{5}}\left( 0 \right) - 9 \amp \implies y=-9\\
y = {\frac{8}{5}}\left( 5 \right) - 9 \amp \implies y=-1\\
y = {\frac{8}{5}}\left( 10 \right) - 9 \amp \implies y=7\\
y = {\frac{8}{5}}\left( 15 \right) - 9 \amp \implies y=15\\
\end{aligned}
\end{equation*}
So the table may be completed as:
| \(x\) | \(y\) |
| \(-5\) | \(-17\) |
| \(0\) | \(-9\) |
| \(5\) | \(-1\) |
| \(10\) | \(7\) |
| \(15\) | \(15\) |
| Values of \(x\) and \(y\) satisfying the equation \(y={\frac{8}{5}}x - 9\) |
Subsection 13.1.2 Graphing Lines in Slope-Intercept Form
Recall that the slope-intercept form of a line equation is \(y=mx+b\) where \(m\) is the slope and \((0,b)\) is the vertical intercept.
Example 13.1.6.
An efficient method to graph \(y=-0.6x+12\) is to use the fact that it is in slope-intercept form. To quickly make a graph, examine the equation and pick out the slope (in this case \(-0.6\)) and vertical intercept (in this case \((0,12)\)), and then plot slope-triangles from the intercept to locate more points on the line. One key point here is that it helps to have the slope written as a fraction. In this case,
\begin{equation*}
-0.6=-\frac{6}{10}=-\frac{3}{5}\text{.}
\end{equation*}
So start our graph at \((0,12)\) and go forward \(5\) units and then down \(3\) units to reach more points.
Since we know that we will go forward \(5\) units and then down \(3\) units, and that we will start our graph at \((0,12)\text{,}\) we can choose to orient and scale our axes to see a more complete picture of \(W\) than we achieved by plotting convenient points in Example 2.
Example 13.1.8.
Find the slope and vertical intercept of \(y=h(x)\text{,}\) where \(h(x)=\frac{5}{3}x-4\text{.}\) Then use slope triangles to find two more points on the line and sketch it.
Explanation.
The slope is \(\frac{5}{3}\) and the vertical intercept is \((0,-4)\text{.}\) Starting at \((0,-4)\text{,}\) we go forward \(3\) units and up \(5\) units to reach more points: \((3,1)\) and \((6,6)\text{.}\)
Subsection 13.1.3 Graphing Lines in Point-Slope Form
Recall that the point-slope form of a line equation is \(y=m(x-x_0)+y_0\) where \(m\) is the slope and \((x_0,y_0)\) is a point on the line. The reason that \((x_0,y_0)\) is a point on the line is because you can substitute in \(x_0\) for \(x\) and then \(y_0\) is the result for \(y\text{.}\)
\begin{equation*}
\underset{\overset{\downarrow}{y_0}}{\strut y \strut}=m(\overset{\overset{x_0}{\downarrow}}{\strut x \strut}-x_0)+y_0
\end{equation*}
Example 13.1.10.
The population of Monarch butterflies has been on an overall downward trajectory since the 1980s, as have populations of many migratory animals. Efforts to restore the population haven’t had great success yet. There are several distinct populations of Monarchs that probably never meet each other: the Hawaii population, the Florida Keys population, the Western population, and the Eastern population. Of these, the Eastern population is by far the largest and we can model this population of Monarch butterflies with a simple linear function.
1
www.fws.gov/midwest/monarch/OverwinteringMonarchs.html
\begin{equation*}
M(x)=-(x-2006)+15
\end{equation*}
approximates the total number of acres of Mexican forest that the Eastern population of Monarchs hibernates in during winter in year \(x\text{.}\) This formula is only valid from 1995 to 2018, the years that the population has been well studied.
Let’s make graph of this equation given the information provided, but only between 1995 and 2018.
Since this formula is linear and given in point-slope form, we can easily read that the slope of the line is \(-1\text{,}\) and the point given by the equation is \((2006,15)\text{.}\) This means that we should scale our graph appropriately to be able to see these details.
We can interpret the point \((2006,15)\) to mean that in the year 2006, the Monarchs overwintered in \(15\) acres of Mexican forest. The slope means that for every one year that goes by, the overwintering population takes up about one less acre of forest.
Example 13.1.12.
Find the slope and a point on the graph of \(y=m(x)\text{,}\) where \(m(x)=-\frac{9}{5}(x+1)-3\text{.}\) Then use slope triangles to find two more points on the line and sketch it.
Explanation.
The slope of the line is \(-\frac{9}{5}\text{,}\) and the point given by the equation is \((-1,-3)\text{.}\) So to graph \(h\text{,}\) start at \((-1,-3)\text{,}\) and the go forward \(5\) units and down \(9\) units to reach more points: \((4,-12)\) and \((9,-21)\text{.}\)
Subsection 13.1.4 Graphing Lines Using Intercepts
Recall that the standard form of a line equation is \(Ax+By=C\) where where \(A\text{,}\) \(B\text{,}\) and \(C\) are three numbers (each of which might be \(0\text{,}\) although at least one of \(A\) and \(B\) must be nonzero).
Example 13.1.14.
Recall our bathtub draining problem from Example 2, where \(W(x)=-0.6x+12\) modeled the amount of water, in gallons, in the tub \(x\) seconds after it started draining. Let’s write the line equation \(y=-0.6x+12\) in standard form.
To find the standard form of the equation, we do as in Subsection 3.7.3. First, we will replace the variable \(W(x)\) with \(y\) because standard form relates \(x\) and \(y\) and does not use function notation. So \(W(x)=-0.6x+12\) becomes \(y=-0.6x+12\text{.}\) Now to convert to standard form, move both \(x\) and \(y\) to the left-hand side.
\begin{align*}
y\amp=-0.6x+12\\
0.6x+y\amp=12
\end{align*}
The equation is in standard form written as \(0.6x+y=12\text{.}\)
If a linear function is given in standard form, we can relative easily find the equation’s \(x\)- and \(y\)-intercepts by substituting in \(y=0\) and \(x=0\text{,}\) respectively.
Example 13.1.15.
Let’s find the intercepts of \(0.6x+y=12\text{,}\) still relating back to Example 2. Then we may graph the equation using those intercepts.
To find the \(x\)-intercept, set \(y=0\) and solve for \(x\text{.}\)
\begin{align*}
0.6x+\substitute{(0)}\amp=12\\
0.6x\amp=12\\
x\amp=20
\end{align*}
So the \(x\)-intercept is the point \((\firsthighlight{20},\secondhighlight{0})\text{.}\) In context, this means that \(\firsthighlight{20}\) minutes after the tub started to drain, \(\secondhighlight{0}\) gallons of water remained. This is telling us that the tub is empty!
To find the \(y\)-intercept, set \(x=0\) and solve for \(y\text{.}\)
\begin{align*}
0.6\substitute{(0)}+y\amp=12\\
y\amp=12
\end{align*}
So, the \(y\)-intercept is the point \((\firsthighlight{0},\secondhighlight{12})\text{.}\) In context, this means that \(\firsthighlight{0}\) minutes after the tub started to drain, \(\secondhighlight{12}\) gallons of water remained. This is telling us how much water was initially in the tub.
When you sketch the graph of a straight line on paper using a straight edge, even having the straight edge off by a very small angle can have a large effect on where the line is drawn, and make your sketch too inaccurate for many purposes. To protect against this, you can find a third point on the line. To that end, we choose \(x=5\text{,}\) then solve for \(y\) in the given equation.
\begin{align*}
0.6(\substitute{5})+y\amp=12\\
3+y\amp=12\\
y\amp=9
\end{align*}
Note we chose \(x=5\) because it would end up with an integer for \(y\text{.}\) So another point on the line must be \((\firsthighlight{5},\secondhighlight{9})\text{.}\) In context, this means that \(\firsthighlight{5}\) minutes after the tub started to drain, \(\secondhighlight{9}\) gallons of water remained.
Now with the \(x\)- and \(y\)-intercepts known along with an additional point, we may plot these points and draw the line that runs through them.
Checkpoint 13.1.17.
Find the \(y\)-intercept and \(x\)-intercept of the line given by the equation. If a particular intercept does not exist, enter
none into all the answer blanks for that row.
\begin{equation*}
2 x + 3 y = -6
\end{equation*}
| \(x\)-value | \(y\)-value | Location (as an ordered pair) | |
| \(y\)-intercept | |||
| \(x\)-intercept |
| \(x\)-intercept and \(y\)-intercept of the line \(2 x+3 y=-6\) |
Explanation.
A line’s \(y\)-intercept is on the \(y\)-axis, implying that its \(x\)-value must be \(0\text{.}\) To find a line’s \(y\)-intercept, we substitute in \(x=0\text{.}\) In this problem we have:
\begin{equation*}
\begin{aligned}
2 x+3 y \amp = -6\\
2 (0)+3 y \amp = -6\\
3 y \amp = -6 \\
\frac{3 y}{3} \amp = \frac{-6}{3}\\
y \amp = -2
\end{aligned}
\end{equation*}
This line’s \(y\)-intercept is \((0,-2)\text{.}\)
Next, a line’s \(x\)-intercept is on the \(x\)-axis, implying that its \(y\)-value must be \(0\text{.}\) To find a line’s \(x\)-intercept, we substitute in \(y=0\text{.}\) In this problem we have:
\begin{equation*}
\begin{aligned}
2 x+3 y \amp = -6\\
2 x+3 (0) \amp = -6\\
2 x \amp = -6\\
\frac{2 x}{2} \amp = \frac{-6}{2}\\
x \amp = -3
\end{aligned}
\end{equation*}
The line’s \(x\)-intercept is \((-3,0)\text{.}\)
The entries for the table are:
| \(x\)-value | \(y\)-value | Location | |
| \(y\)-intercept | \(0\) | \(-2\) | \((0,-2)\) |
| \(x\)-intercept | \(-3\) | \(0\) | \((-3,0)\) |
| \(x\)-intercept and \(y\)-intercept of the line \(2 x+3 y=-6\) |
Subsection 13.1.5 Graphing Functions by Plotting Points
Any function, linear or not, can be graphed by building a table of \(x\)- and \(y\)-values and plotting points. Let’s look at a few more examples.
Example 13.1.18.
Imagine a company called Corduroy’s-Я-Us that makes pants. Their profit from their Royal Blue Corduroys, in thousands of dollars, can be modeled by the function \(P(x)=-0.5x^2+33x-200\) where \(x\) is the price of each pair of Royal Blue pants that they sell. Let’s build a table of values and plot the function’s graph.
In this context, the value of \(x\) must be positive. Furthermore, we shouldn’t really consider \(x\)-values like \(1\text{,}\) \(2\text{,}\) etc., because it is not realistic that the price of a pair of new pants would be so low. Instead we try multiples of \(10\text{:}\) \(10\text{,}\) \(20\text{,}\) etc.
| \(x\) | \(P(x)=-0.5x^2+33x-200\) | Point | Interpretation |
| \(0\) |
\(-0.5(0)^2+33(0)-200\) \({}=-200\) |
\((0,-200)\) | If each pair costs \(\$0\text{,}\) there is a loss of \(\$200{,}000\text{.}\)
|
| \(10\) |
\(-0.5(10)^2+33(10)-200\) \({}=80\) |
\((10,80)\) | If each pair costs \(\$10\text{,}\) the profit is \(\$80{,}000.\)
|
| \(20\) |
\(-0.5(20)^2+33(20)-200\) \({}=260\) |
\((20,260)\) | If each pair costs \(\$20\text{,}\) the profit is \(\$260{,}000\text{.}\)
|
| \(30\) |
\(-0.5(30)^2+33(30)-200\) \({}=340\) |
\((30,340)\) | If each pair costs \(\$30\text{,}\) the profit is \(\$340{,}000\text{.}\)
|
| \(40\) |
\(-0.5(40)^2+33(40)-200\) \({}=320\) |
\((40,320)\) | If each pair costs \(\$40\text{,}\) the profit is \(\$320{,}000\text{.}\)
|
| \(50\) |
\(-0.5(50)^2+33(50)-200\) \({}=200\) |
\((50,200)\) | If each pair costs \(\$50\text{,}\) the profit is \(\$200{,}000\text{.}\)
|
| \(60\) |
\(-0.5(60)^2+33(60)-200\) \({}=-20\) |
\((60,-20)\) | If each pair costs \(\$60\text{,}\) there is a loss of \(\$20{,}000\text{.}\)
|
With the values in Table 19, we can sketch the graph. Note that we have to estimate the how the graph curves which is a limitation of graphing a function by plotting points compared with using algebraic techniques.
Checkpoint 13.1.21.
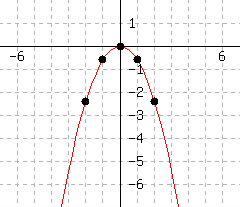
Make a table of solutions for the equation \({y}={-0.6x^{2}}\text{.}\) Then graph the equation.
| \(x\) | \(y\) |
| Values of \(x\) and \(y\) satisfying the equation \(y=-0.6x^{2}\) |
Explanation.
This solution will use the \(x\) values \(-2\text{,}\) \(-1\text{,}\) \(0\text{,}\) \(1\) and \(2\text{.}\) The choice to use these \(x\)-values is arbitrary. Since they are small numbers, they might make calculations easier. It’s important to include negative numbers.
One at a time, we substitute these \(x\)-values into the equation \(y=-0.6x^{2}\text{,}\) and solve for \(y\)
\begin{equation*}
\begin{aligned}
y = -0.6\mathopen{}\left(-2\right)^{2} \amp \implies y=-2.4\\
y = -0.6\mathopen{}\left(-1\right)^{2} \amp \implies y=-0.6\\
y = -0.6\cdot 0^{2} \amp \implies y=0\\
y = -0.6\cdot 1^{2} \amp \implies y=-0.6\\
y = -0.6\cdot 2^{2} \amp \implies y=-2.4\\
\end{aligned}
\end{equation*}
So the table may be completed as:
| \(x\) | \(y\) |
| \(-2\) | \(-2.4\) |
| \(-1\) | \(-0.6\) |
| \(0\) | \(0\) |
| \(1\) | \(-0.6\) |
| \(2\) | \(-2.4\) |
| Values of \(x\) and \(y\) satisfying the equation \(y=-0.6x^{2}\) |
Using the values in the table, we can plot the following graph.
Example 13.1.22.
Human-initiated global warming has been the subject of some debate. However, one aspect of the debate is undeniable fact: the amount of atmospheric carbon dioxide (\(\mathrm{CO}_2\text{:}\) a greenhouse gas) is being regularly and carefully measured and is increasing faster and faster. The measured yearly average atmospheric carbon dioxide levels in parts per million (ppm) since 1958 can be very closely approximated by the function \(C(x)=244+29\cdot1.0148^x\) where \(x\) represents the number of years since the year 1900. Before 1958, the greenhouse gases weren’t regularly measured. Create a table of values rounded to the nearest whole number for the carbon dioxide levels since 1958.
2
www.epa.gov/ghgemissions/overview-greenhouse-gases3
esrl.noaa.gov/gmd/ccgg/trends/graph.htmlExplanation.
Since 1958 is \(58\) years since 1900, we will start our table at \(x=58\) and go by \(10\)s up through \(x=118\text{,}\) which would stand for the year 2018.
| \(x\) | \(C(x)\) | Point | Interpretation |
| \(58\) | \(w(58)\approx312\) | \((5,312)\) | In 1958, the atmosphere was about \(312\) ppm \(\mathrm{CO}_2\text{.}\)
|
| \(68\) | \(w(68)\approx323\) | \((68,323)\) | In 1968, the atmosphere was about \(323\) ppm \(\mathrm{CO}_2\text{.}\)
|
| \(78\) | \(w(78)\approx335\) | \((78,335)\) | In 1978, the atmosphere was about \(335\) ppm \(\mathrm{CO}_2\text{.}\)
|
| \(88\) | \(w(88)\approx350\) | \((88,350)\) | In 1988, the atmosphere was about \(350\) ppm \(\mathrm{CO}_2\text{.}\)
|
| \(98\) | \(w(98)\approx366\) | \((98,366)\) | In 1998, the atmosphere was about \(366\) ppm \(\mathrm{CO}_2\text{.}\)
|
| \(108\) | \(w(108)\approx386\) | \((108,386)\) | In 2008, the atmosphere was about \(386\) ppm \(\mathrm{CO}_2\text{.}\)
|
| \(118\) | \(w(118)\approx408\) | \((118,408)\) | In 2018, the atmosphere was about \(408\) ppm \(\mathrm{CO}_2\text{.}\)
|
4
www.esrl.noaa.gov/gmd/ccgg/trends/graph.htmlReading Questions 13.1.6 Reading Questions
1.
What are the four methods we recalled to graph lines in this section?
2.
Why might it be better to represent a line in point-slope form than slope intercept form?
3.
Explain how an equation for a line given in slope-intercept or point-slope form can be graphed without creating a table of values.
4.
Describe one or more possible issues you might encounter after creating a table of points for a function and trying to use those points to make a graph.
Exercises 13.1.7 Exercises
Graphing Lines by Plotting Points.
Create a table of ordered pairs and then make a plot of the equation.
1.
\(y=2x+3\)
2.
\(y=3x+5\)
3.
\(y=-\frac{2}{5}x-3\)
4.
\(y=-\frac{3}{4}x+2\)
Graphing Lines in Slope-Intercept Form.
5.
Graph the equation \(y=\frac{2}{3}x+4\text{.}\)
6.
Graph the equation \(y=\frac{3}{2}x-5\text{.}\)
7.
Graph the equation \(y=-\frac{3}{5}x-1\text{.}\)
8.
Graph the equation \(y=-\frac{1}{5}x+1\text{.}\)
Graphing Lines in Point-Slope Form.
9.
Graph the linear equation \(y=-\frac{8}{3}(x-4)-5\) by identifying the slope and one point on this line.
10.
Graph the linear equation \(y=\frac{5}{7}(x+3)+2\) by identifying the slope and one point on this line.
11.
Graph the linear equation \(y=\frac{3}{4}(x+2)+1\) by identifying the slope and one point on this line.
12.
Graph the linear equation \(y=-\frac{5}{2}(x-1)-5\) by identifying the slope and one point on this line.
13.
Graph the linear equation \(y=-3(x-9)+4\) by identifying the slope and one point on this line.
14.
Graph the linear equation \(y=7(x+3)-10\) by identifying the slope and one point on this line.
Graphing Lines Using Intercepts.
15.
Find the \(x\)- and \(y\)-intercepts of the line with equation \(5x-2y=10\text{.}\) Then find one other point on the line. Use your results to graph the line.
16.
Find the \(x\)- and \(y\)-intercepts of the line with equation \(5x-6y=-90\text{.}\) Then find one other point on the line. Use your results to graph the line.
17.
Find the \(x\)- and \(y\)-intercepts of the line with equation \(x+5y=-15\text{.}\) Then find one other point on the line. Use your results to graph the line.
18.
Find the \(x\)- and \(y\)-intercepts of the line with equation \(6x+y=-18\text{.}\) Then find one other point on the line. Use your results to graph the line.
19.
Make a graph of the line \(-5x-y=-3\text{.}\)
20.
Make a graph of the line \(x+5y=5\text{.}\)
21.
Make a graph of the line \(20x-4y=8\text{.}\)
22.
Make a graph of the line \(3x+5y=10\text{.}\)
Graphing Functions by Plotting Points.
Create a table of ordered pairs and then make a plot of the equation.
23.
\(y=-3x^2\)
24.
\(y=-x^2-2x-3\)
25.
\(y=\frac{1}{2}x^3-x\)
26.
\(y=\frac{1}{4}x^3+x+2\)
27.
\(y=\sqrt{x+5}\)
28.
\(y=3-\sqrt{x+2}\)
You have attempted of activities on this page.

