Probability Detour - Normal Random Variables.
Many quantitative variables have a distribution that can be reasonably modeled with a normal probability curve. This is a continuous probability distribution (as opposed to the binomial, which is a discrete distribution) that is specified by two quantities:
-
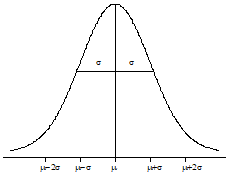
Mean, denoted by \(\mu\) ("mu"), which is the peak and point of symmetry
-
Standard deviation, denoted by \(\sigma\) ("sigma"), which is the distance between the mean and each inflection point
In other words, the mean determines the center of the distribution, and the standard deviation controls how variable (spread out) the distribution is. The standard deviation can be loosely interpreted as a typical distance of the observations from the mean.
This normal curve is given by the following function:
\(N(\mu, \sigma): f(x) = \frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{1}{2}\left(\frac{x-\mu}{\sigma}\right)^2}\text{,}\) \(-\infty < x < \infty\)
Notes: The symbol \(\pi\) is used here to refer to the irrational number \(\approx 3.14159\ldots\text{.}\) The constant in front of the exponential term ensures that the total area under any normal curve equals one.
Probability calculations: Then the probability of an observation falling in any particular interval on the x-axis is determined by the area under the normal curve over that interval. In principle, this area could be determined by integrating the function \(f(x)\) above the interval. However, this particular function has no closed form anti-derivative, so we rely on technology to approximate these areas and therefore these normal probabilities.
The empirical rule: For a mound-shaped, symmetric distribution (like the normal) with mean \(\mu\) and standard deviation \(\sigma\text{,}\)
-
the interval \((\mu - \sigma, \mu + \sigma)\) should capture approximately 68% of the distribution.
-
the interval \((\mu - 2\sigma, \mu + 2\sigma)\) should capture approximately 95% of the distribution.
-
the interval \((\mu - 3\sigma, \mu + 3\sigma)\) should capture approximately 99.7% of the distribution.
