Investigation 2.8: Turbidity

Section 8.2 Investigation 2.8: Turbidity

Another measure of water quality is turbidity, the degree of opaqueness produced in water by suspended particulate matter. Turbidity can be measured by seeing how light is scattered and/or absorbed by organic and inorganic material. Larger nephelometric turbidity units (NTU) indicate increased turbidity and decreased light penetration. If there is too much turbidity, then not enough light may be penetrating the water, affecting photosynthesis to the surface and leading to less dissolved oxygen.

🔗

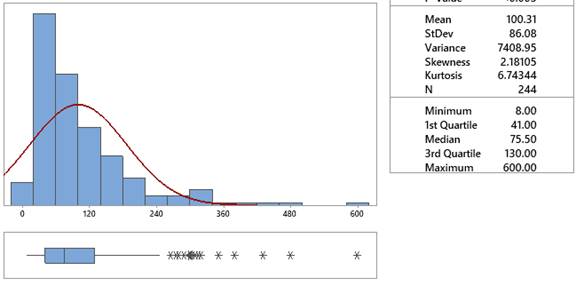
CRiggs (2002) provides 244 turbidity monthly readings that were recorded between 1980-2000 from a reach of the Mermentau River in Southwest Louisiana (MermentauTurbidity.txt). The unit of analysis was the monthly mean turbidity (NTU) computed from each month’s systematic sample of 21 turbidity measurements. The investigators wanted to determine whether the mean turbidity was greater than the local criterion value of 150 NTU.

🔗

Checkpoint 8.2.1. Analyze original turbidity distribution.

Find the mean and median of the turbidity measurements and confirm that a normal probability is not reasonable for these data.

🔗

Mean: NTU

🔗

Median: NTU

🔗

Is a normal distribution reasonable?

🔗

Solution.

The mean is 100.31 NTU and the median is 75.50 NTU. The distribution is skewed to the right and not well modelled by a normal distribution.

🔗

Descriptive statistics and histogram for turbidity data

🔗

Checkpoint 8.2.2. Apply log transformation.

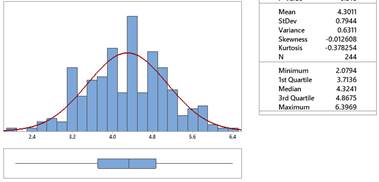
Carry out a log transformation (See Section 6.2) and report the mean, median, and standard deviation of the transformed data. Verify that a log-normal probability model is reasonable for these data.

🔗

Solution.

The log-turbidity values are reasonably well modeled by a normal distribution, with mean 4.3011 log NTU and median 4.3241 log NTU.

🔗

(We could also compare the original observations to the log normal distribution.)

🔗

Descriptive statistics and histogram for log-transformed turbidity data

🔗

Checkpoint 8.2.3. Compare original and transformed statistics.

Are the mean and median values in checkpoint 8.2.2 similar to each other? Is the mean of the logged turbidity values similar to the log of the mean of the turbidity values? Is the median of the logged turbidity values similar to the log of the median of the turbidity values?

🔗

Table 8.2.4. Comparison of Original and Transformed Values

🔗

Original scale	Log of original values	Transformed scale
Mean =	Log (mean) =	Mean (log turbidity) =
Median =	Log (median) =	Median (log turbidity) =

Explanation:

🔗

Solution.

The mean and median values in (b) are similar as we would expect with the transformed data now being symmetric.

🔗

The median turbidity value (before transforming) was 75.5. The natural log of this value is 4.3241. This is the same as the median of the log-turbidity values.

🔗

The mean turbidity value (before transforming) was 100.307. The natural log of this value is 4.6082, which is not the same as the mean of the log-turbidity values.

🔗

Table 8.2.5. Completed Comparison Table

🔗

Original scale	Log of original values	Transformed scale
Mean = 100.3	Log (mean) = 4.608	Mean (log turbidity) = 4.301
Median = 75.5	Log (median) = 4.324	Median (log turbidity) = 4.324

🔗

Checkpoint 8.2.6. Explain median vs. mean transformation.

Explain why the median(log(turbidity)) is expected to be the same as log(median(turbidity)), but this interchangeability is not expected to work for the mean.

🔗

Solution.

We expect the medians to match because the median is essentially the middle value (slightly untrue with an even number of observations) and the same observation will still be the median value after the log transformation. However, the mean utilizes the numerical values and the relative distances between observations is changed with the log transformation.

🔗

Checkpoint 8.2.7. Calculate confidence interval for transformed data.

Use a one-sample t-confidence interval to estimate the mean of the log-turbidity value for this river.

🔗

Solution.

We are 95% confident the population mean (so also the population median with symmetric data) is in this interval.

🔗

🔗

Checkpoint 8.2.8. Back-transform and interpret interval.

Back-transform the endpoints of this interval to return to the original units and interpret the interval in context.

🔗

Solution.

(exp population median ln turbidity) = (exp ln population median turbidity) = population median turbidity

🔗

\(e^{4.2009} = 66.75\)

🔗

\(e^{4.4013} = 81.56\)

🔗

We are 95% confident that the population median turbidity for this river as a whole is between 66.75 and 81.56 NTU.

🔗

Discussion: Transformations and Back-Transformation.

Once you create a symmetric distribution, the mean and median will be similar. However, although transforming the data does not affect the ordering of the observations, it does impact the scaling of the values. So whereas the median of the transformed data is equal to taking the log of the median of the original data (at least with an odd number of observations), this does not hold for the mean. So when we back-transform our interval for the center of the population distribution, we will interpret this in terms of the median value rather than the mean value.

🔗

Study Conclusions.

A 95% confidence interval based on the transformed data equals (4.20, 4.40). Therefore, we will say we are 95% confident that the median turbidity in this river is between 66.69 NTU and 81.45 NTU, clearly less than the 150 NTU regulation. However, another condition for the validity of this procedure is that the observations are independent. Further examination of these data reveals seasonal trends. Adjustments need to be made to account for the seasonality before these data are analyzed.

🔗