Section 12.2 Investigation 3.6: Is Yawning Contagious?
The folks at MythBusters, a popular television program on the Discovery Channel, investigated whether yawning is contagious by recruiting fifty subjects at a local flea market and asking them to sit in one of three small rooms for a short period of time. Video snippet

For some of the subjects, the attendee yawned while leading them to two of the rooms (planting a yawn "seed"), whereas for the other subjects the attendee did not yawn. As time passed, the researchers watched (via a hidden camera) to see which subjects yawned.
Checkpoint 12.2.1. Identify Variables.
Checkpoint 12.2.2. State Hypotheses.
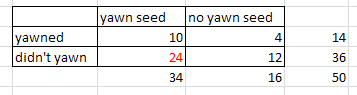
In the study they found that 10 of 34 subjects who had been given a yawn seed actually yawned themselves, compared with 4 of 16 subjects who had not been given a yawn seed.
Checkpoint 12.2.3. Create Two-Way Table.
Checkpoint 12.2.6. Design Simulation.
Open the Analyzing Two-way Tables applet.
-
Paste in the raw data and press Use Data or enter the titles and counts of a two-way table and press Use Table. (Or check the 2×2 box and enter the cell values and headers)
-
Select GroupA Successes as the statistic.
-
(Scroll right) Generate a randomization distribution for this statistic.
-
Check the Show Shuffle Options box.
-
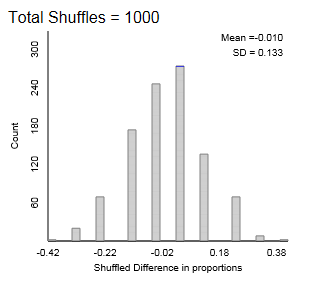
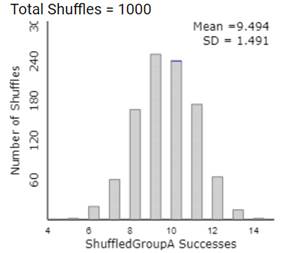
Set Number of Shuffles to 1000.
-
Press Shuffle.
Checkpoint 12.2.7. Describe Randomization Distribution.
Checkpoint 12.2.8. Estimate p-value.
-
Specify the observed number of successes in the Count Samples box.
-
Then indicate whether the research conjecture expected a larger or smaller number of successes in the seed treatment by choosing Greater Than or Less Than from the pull-down menu.
-
Then press the Count button.
Report your p-value:
Exact p-value.
The simulations you have conducted in Investigations 3.5 (Dolphin Therapy) and above approximated the p-value for two-way tables arising from random assignment by assuming the row and column totals are fixed. In this case, the probability of obtaining a specific number of successes in one group can be calculated exactly using the hypergeometric probability distribution. (We used the independent binomial distributions with the teen hearing loss study, where we wanted to sample separately from two populations and the overall number of successes was not fixed in advance.)
Keep in mind, that under the null hypothesis, we are assuming the group assignments made no difference and that there would be 14 successes ("yawners") and 36 failures ("non-yawners") between the two groups regardless.
Because the random assignment makes every configuration of the subjects between the two groups equally likely, we determine the probability of any particular outcome for the number of yawners and non-yawners by first counting the total number of ways to assign 34 of the subjects to the yawn-seed group (and 16 to the no-yawn-seed group) in the denominator. The numerator is then the number of ways to get a particular set of configurations for that group, such as those consisting of 10 yawners and 24 non-yawners.
Checkpoint 12.2.9. Total Ways to Assign.
How many ways altogether are there to randomly assign these 50 subjects into one group of 34 (yawn-seed group) and the remaining group of 16 (no-yawn-seed group)?
Hint.
Checkpoint 12.2.10. Ways to Obtain Observed Configuration.
Now consider the 14 successes and the 36 failures.
How many ways are there to randomly select 10 of the successes?
Successes:
How many ways are there to randomly assign 24 of the failures to be in the yawn seed group?
Failures:
How should you combine these two numbers to calculate the total number of ways to obtain 10 successes and 24 failures in the yawn-seed group, the configuration that we observed in the study?
Total:
Checkpoint 12.2.11. Calculate Exact Probability.
To determine the exact probability that random assignment would produce exactly 10 successes and 24 failures into the group of 34 subjects, divide your calculation in checkpoint 9 by your calculation in checkpoint 8.
Hint.
Checkpoint 12.2.12. Is this the p-value?
Hypergeometric Distribution.
The probability of obtaining \(k\) successes in Group A, with \(n\) observations, when sampled from a two-way table with \(N\) observations, consisting of \(M\) successes and \(N - M\) failures is:
\begin{equation*}
P(X = k) = \frac{C(M, k) \times C(N - M, n - k)}{C(N, n)}
\end{equation*}
where \(C(N, n) = \frac{N!}{n!(N - n)!}\) is the number of ways to choose \(n\) items from a group of \(N\) items, and \(X\) represents the number of successes randomly selected for group A. \(X\) is a hypergeometric random variable. Also note \(E(X) = n(M/N)\) and \(SD(X) = \sqrt{n(M/N)(1 - M/N)(N - n)/(N - 1)}\text{.}\)
In this study, we had \(N = 50\) subjects and we defined yawning to be success so \(M = 14\text{.}\) We also arbitrarily chose to focus on the yawn-seed group, so \(n = 34\text{.}\) This calculation works out the same if you had defined "not yawning" to be a success and/or if you had focused on the 16 people in the no-yawn-seed group. You just need to make sure you count consistently.
We will continue to define the p-value to be the probability of obtaining results at least as extreme as those observed in the actual study. Because we expected more yawners in the yawn-seed group, the p-value is the probability of randomly assigning at least 10 of the yawners in the yawn-seed group.
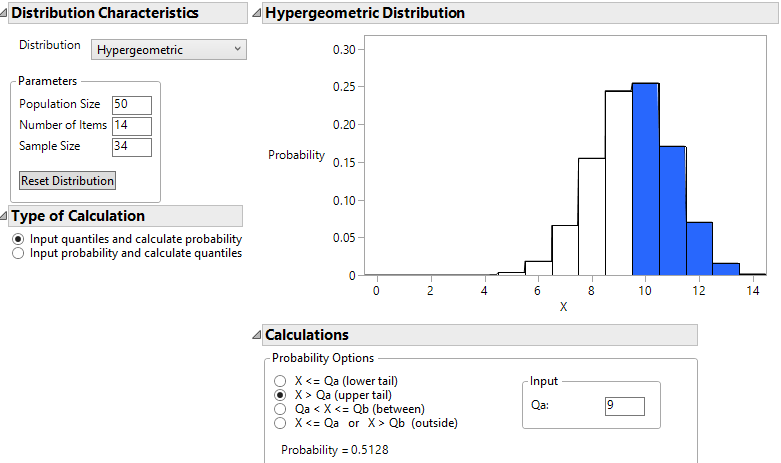
So far you have found \(P(X = 10) = C(14, 10) \times C(36, 24) / C(50, 34) = 0.2545\text{.}\)
Checkpoint 12.2.13. Calculate Additional Probabilities.
Checkpoint 12.2.14. Exact p-value and Interpretation.
Sum all five probabilities together (including P(X = 10)) to determine the exact p-value for the yawning study. How does this p-value compare to the empirical p-value from the applet simulation? Write a one or two sentence interpretation of this p-value.
Exact p-value:
Comparison:
Interpretation:
Solution.
Exact p-value: 0.254 + 0.1708 + 0.0702 + 0.0158 + 0.0015 = 0.5128
Comparison: similar to simulation
Interpretation: P(X ≥ 10), probability of 10 or more successes by random assignment alone (assuming no effect from the seed). If the yawn seed has no effect, the probability of finding 10 or more of 34 yawners in the seeded group when 50 subjects are randomly assigned to seeded and no-seed groups is 0.5128.
Definition: Fisher’s Exact Test.
Using the hypergeometric probabilities to determine a p-value in this fashion for a two-way table is called Fisher’s Exact Test, named after R. A. Fisher.
Technology Detour – Calculating Hypergeometric Probabilities (Fisher’s Exact Test).
Checkpoint 12.2.15. Calculating Hypergeometric Probabilities in Analyzing Two-way Tables applet.
Checkpoint 12.2.16. Calculating Hypergeometric Probabilities in R.
The iscamhyperprob function takes the following inputs:
-
k, the observed value of interest (or the difference in conditional proportions, assumed if value is less than one, including negative) -
total, the total number of observations in the two-way table -
succ, the overall number of successes in the table -
n, the number of observations in "group A" -
lower.tail, a Boolean which is TRUE or FALSE
For example:
iscamhyperprob(k=10, total=50, succ=14, n=34, lower.tail=FALSE)
Checkpoint 12.2.17. Calculating Hypergeometric Probabilities in JMP.
Using the Distribution Calculator:
-
Choose Hypergeometric from the Distribution menu
-
Specify the values of Population Size = table total, Number of Items = total number of successes, Sample Size = group 1 total
-
Select Input quantiles and compute probabilities
-
Specify the tail probability and enter Qa = number of successes in "group A"
Checkpoint 12.2.18. Technology Calculation.
Checkpoint 12.2.19. Alternative Setup - Not Yawning.
Checkpoint 12.2.20. Alternative Setup - No Seed Group.
Discussion.
You should see that there are several equivalent ways to set up the probability calculation. Make sure it is clear how you define success/failure and which group you are considering "group A." This will help you determine the numerical values for \(N\text{,}\) \(M\text{,}\) and \(n\) in the calculation.
Below is a graph of the Hypergeometric distribution with \(N = 50\text{,}\) \(M = 14\text{,}\) and \(n = 34\text{.}\)
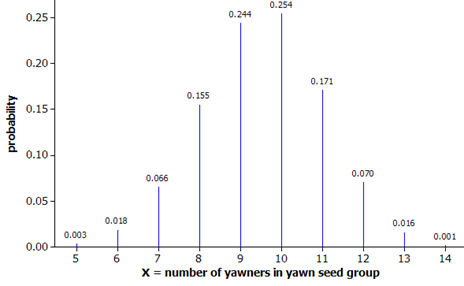
Using probability rules, you can show that the expected value of this distribution is \(\mu = (14/50) \times 34 = 9.52\) yawners in yawn seed group and the standard deviation of the probability distribution is the square root of \(n \times (M/N) \times (N – M)/N \times (N – n)/(N – 1) = 1.496\) yawners.
Checkpoint 12.2.21. Compare to Simulation.
Checkpoint 12.2.22. MythBusters Conclusion.
Checkpoint 12.2.23. Generalizability.
Study Conclusions.
With a large p-value of 0.513 (Fisher’s Exact Test), we do not have any evidence that the difference between the two groups (with and without yawn seed) was created from something other than the random assignment process. If there was nothing to the theory that yawning is contagious, by "luck of the draw" alone, we would expect 10 or more of the yawners to end up in the yawn seed group in more than 50% of random assignments. Although the study results were in the conjectured direction, the difference between the yawning proportions was not large enough to convince us that the probability of yawning is truly larger when a yawn seed is planted. The researchers could try the study again with a larger sample size to increase the power of their test. The researchers also may want to be cautious in generalizing these results beyond the population of volunteers at a local flea market or how naturalistic the setting of leading individuals to a small room to wait is.
Subsection 12.2.1 Practice Problem 3.6A
Checkpoint 12.2.24. Evidence Against Contagious Yawning.
Checkpoint 12.2.25. Sample Size and Power.
Checkpoint 12.2.26. Hypergeometric vs Binomial.
Subsection 12.2.2 Practice Problem 3.6B
Reconsider the Dolphin Therapy study (Investigation 3.5).
| Dolphin Therapy | Control Group | Total | |
|---|---|---|---|
| Showed substantial improvement | 10 | 3 | 13 |
| Did not show substantial improvement | 5 | 12 | 17 |
| Total | 15 | 15 | 30 |
Continue to focus on the number of improvers randomly assigned to the dolphin group, and represent this value by X.
Checkpoint 12.2.28. Hypergeometric Parameters.
Checkpoint 12.2.29. Setup for Exact p-value.
Checkpoint 12.2.30. Calculate Exact p-value.
Checkpoint 12.2.31. Double the Sample Size.
Suppose that the dolphin study had involved twice as many subjects, again with half randomly assigned to each group, and with the same proportion of improvers in each group. Determine the exact p-value in this case, and comment on whether/how it changes from the p-value with the real data. Explain why this makes sense.
Subsection 12.2.3 Practice Problem 3.6C
Checkpoint 12.2.32. Alternative Setup - Not Yawning.
Checkpoint 12.2.33. Technology Calculation - Non-yawners.
Checkpoint 12.2.34. No Seed Group Probability.
Suppose I want to find the probability of 4 or fewer yawners in the No Seed group. Identify the values of \(N\text{,}\) \(M\text{,}\) \(n\text{,}\) and \(k\text{.}\) Use technology to calculate the probability of 4 or fewer yawners in the No Seed group using the hypergeometric distribution. (Include readable output.)
Checkpoint 12.2.35. Importance of Blinding.
Checkpoint 12.2.36. Unequal Sample Sizes.
You have attempted of activities on this page.