Example: Drawing (Recursive) Fractals

Section 12.5 Example: Drawing (Recursive) Fractals

A fractal is a geometric shape that exhibits a recursive structure. When it is divided into parts, each part is a smaller version of the whole.

🔗

Fractal patterns occur in many situations and places. For example, if you look at a graph of the Dow Jones Industrial Average (DJIA) over the past year, the graph for each day is similar to the graph of each month, which is similar to the graph of each year, and so on. Each part is a reduced-scale version of the whole.

🔗

Fractals also occur throughout nature. If you look at a coastline from an airplane, the shape of each part of the coastline, no matter how small the scale, resembles the shape of the whole coastline. If you look at a tree, each branch of the tree is similar in shape to the whole tree.

🔗

So, fractal patterns are all around us. Because of their self-similarity and divisibility, fractals are well-suited for recursive programming. Drawing recursive patterns is also an excellent way to illustrate how to use parameters to create generality in method design.

🔗

In this section, we will develop two simple patterns and incorporate them into a GUI.

🔗

Subsection 12.5.1 Nested Squares

Earlier in this chapter, we developed a recursive definition for drawing a nested squares pattern (Figure 12.2.3). Now let’s develop a recursive method that actually draws the pattern. For this pattern, the base case is the drawing of the square. The recursive case, if more divisions are desired, is the drawing of smaller patterns within the square:

🔗

Algorithm 12.5.1. Nested squares.

Draw a square.
If more divisions are desired
    draw a smaller version of pattern within square.

🔗

An important consideration for this algorithm is to specify precisely what we mean by “if more divisions are desired.” In other words, how exactly do we control the recursion? In our earlier definition of the pattern, we used the length of the side to control the algorithm. When

s i d e \geq 5,

we recursed.

🔗

Another more general way to do this is to describe the fractal structure in terms of its levels. For nested squares, the level-zero pattern would be just the basic square shape (Figure 12.5.2). A level-one pattern would be the basic square shape plus an inner square, and so on. The higher the level, the more subdividing we do. Therefore, one way to control the recursion is to use a level parameter as the recursion parameter—as the parameter that controls the recursion:

🔗

Algorithm 12.5.3. Level based nested squares.

Draw a square.
If the level is greater than 0,
    draw a smaller version of pattern within square.

🔗

What other parameters will we need for this method? If we’re going to draw a rectangle, we’ll need parameters for its x- and y-coordinates. We’ll also need a parameter for the length of sides of the square. Another issue we need to decide is how much the length of the sides should change at each level. Should length change by a fixed amount, by a fixed ratio, or by some other factor? In order to allow this kind of flexibility, let’s use another parameter for this value.

🔗

These design considerations suggest the method shown in Listing 12.5.4. Note that we must also provide a Graphics parameter so the method can use the drawRect() method to draw the square. As we decided, the level parameter controls the recursion. Note that its value is decreased by 1 in the recursive call. This will ensure that level will eventually reach 0, and recursion will stop.

🔗

Listing 12.5.4. The drawBoxes() method.

🔗

/**
 * drawBoxes()---recursively draws pattern of nested
 *  squares with top left corner of outer square at
 *  (locX, locY) and dimensions of length side.
 * level (>= 0) is the recursion parameter (base: = 0)
 * delta is used to adjust the length of the side.
 */
private void drawBoxes(Graphics g, int level,
           int locX, int locY, int side, int delta) {
  g.drawRect(locX, locY, side, side );
  if (level > 0) {
    int newLocX = locX + delta; 
    int newLocY = locY + delta;
    drawBoxes(g, level - 1, newLocX, newLocY, side - 2 * delta, delta);
  } // if
} // drawBoxes()

Finally, note the use of the delta parameter, which is used to change the length of the sides by a fixed amount, 2 * delta, at each level. It is also used to calculate the x- and y-coordinates for the location of the next level of boxes (locX + delta, locY + delta). But delta’s value remains constant through all the levels. This will lead to a pattern where the “gap” between nested squares is constant.

🔗

Principle 12.5.5. EFFECTIVE DESIGN: Levels of Recursion.

Many recursive algorithms use a level parameter as the recursion parameter.

🔗

Exercises Self-Study Exercises

1. Nested Boxes.

The code here combines the drawBoxes() method with a simple GUI to draw a level-9 picture of the nested boxes.

🔗

Modify the level variable and re-run the program to draw different levels of the boxes.
Replace the recursive method with an equivalent iterative method. Hint: On each iteration, you must change the x- and y-coordinates of the square’s location and the length of its side.)

🔗

Subsection 12.5.2 The Sierpinski Gasket

Let’s return now to the Sierpinski gasket pattern that we introduced at the start of this chapter. This is a much more interesting fractal pattern (Fig. Figure 12.5.6). The overall shape of the pattern is that of a triangle, but notice how the outer triangle is divided into three smaller triangles. Then each of those triangles are divided into three smaller triangles. If you continue this process of dividing and shrinking, you get the level-seven pattern shown here.

🔗

Figure 12.5.6. Levels 0, 1, and 7 of the Sierpinski gasket fractal pattern.
🔗

Let’s develop a recursive method to draw this pattern. If we follow the same strategy we used in the nested squares example, we get the following algorithm:

🔗

Algorithm 12.5.7. Sierpinski Gasket.

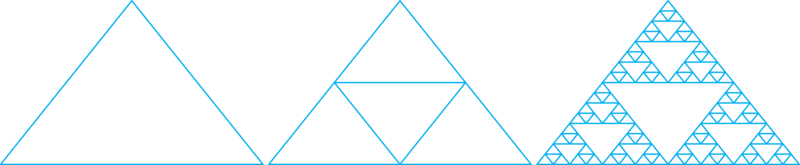
Base case:       Draw a triangle.
Recursive Case:  If more divisions are desired,
     draw three smaller gaskets within the triangle.

🔗

For this pattern the base case is the drawing of the basic triangle. The recursive cases, if more divisions are desired, are the drawing of smaller gaskets within the triangle. Again we will use a level parameter to control the depth of the recursion. The higher the level, the more divisions will be drawn.

🔗

If we’re going to draw a triangle shape, we need the coordinates of its three vertices—that is, an x- and y-coordinate for each vertex. Taken together, these design considerations suggest the method definition shown in Figure 12.5.8.

🔗

/**
 * drawGasket()---recursively draws the Sierpinski gasket
 *  pattern, with points (p1X, p1Y),(p2X, p2Y),(p3X, p3Y)
 *  representing the vertices of its enclosing triangle.
 * level (>= 0) is the recursion parameter (base: = 0)
 */
private void drawGasket(Graphics g, int lev, int p1X, int p1Y,
                   int p2X, int p2Y, int p3X, int p3Y) {
    g.drawLine(p1X, p1Y, p2X, p2Y);  // Draw a triangle
    g.drawLine(p2X, p2Y, p3X, p3Y);
    g.drawLine(p3X, p3Y, p1X, p1Y);
    if (lev > 0) { // If more levels, draw 3 smaller gaskets
      int q1X = (p1X + p2X) / 2;    int q1Y = (p1Y + p2Y) / 2;
      int q2X = (p1X + p3X) / 2;    int q2Y = (p1Y + p3Y) / 2;
      int q3X = (p2X + p3X) / 2;    int q3Y = (p2Y + p3Y) / 2;
      drawGasket(g, lev - 1, p1X, p1Y, q1X, q1Y, q2X, q2Y);
      drawGasket(g, lev - 1, p2X, p2Y, q1X, q1Y, q3X, q3Y);
      drawGasket(g, lev - 1, p3X, p3Y, q2X, q2Y, q3X, q3Y);
    } // if
} // drawGasket()

Figure 12.5.8. The drawGasket() method.

🔗

As we described earlier, we use the level parameter as the recursion parameter for this method, which controls the recursion. Note that each of the three recursive calls decreases the level by 1. This will ensure that eventually level will equal 0, and recursion will stop.

🔗

Note also how the three pairs of coordinates are used. Drawing a triangle is simple. Just draw three lines from (p1X,p1Y) to (p2X,p2Y), from (p2X,p2Y) to (p3X,p3Y), and from (p3X,p3Y) back to (p1X, p1Y).

🔗

The most complicated part of the method is calculating the vertices for the three inner gaskets. If you look at Figure 12.5.6 again, you’ll notice that each of the inner triangles uses one of the vertices of the main triangle, plus the midpoints of the two adjacent sides. Thus, the triangle on the “left” uses the left vertex (p1X,p1Y), and the midpoints of the other two lines from (p1X,p1Y) to (p2X,p2Y) and from (p1X,p1Y) to (p3X,p3Y). As you might remember from high school math, the formula for computing the midpoint of the line segment

(x 1, y 1)

(x 2, y 2)

🔗

Algorithm 12.5.9. Midpoint of a Line.

( (x1 + x2) / 2, (y1 + y2) / 2 )

🔗

This formula is used repeatedly to calculate the vertices of the three smaller gaskets.

🔗

Activity 12.5.1. Sierpinski Gasket.

import javax.swing.*;
import java.awt.*;

public class Triangles extends Canvas {

private int level = 9;

/**
 * drawGasket()---recursively draws the Sierpinski gasket
 *  pattern, with points (p1X, p1Y),(p2X, p2Y),(p3X, p3Y)
 *  representing the vertices of its enclosing triangle.
 * level (>= 0) is the recursion parameter (base: = 0)
 */
private void drawGasket(Graphics g, int lev, int p1X, int p1Y,
                   int p2X, int p2Y, int p3X, int p3Y) {
    g.drawLine(p1X, p1Y, p2X, p2Y);  // Draw a triangle
    g.drawLine(p2X, p2Y, p3X, p3Y);
    g.drawLine(p3X, p3Y, p1X, p1Y);
    if (lev > 0) { // If more levels, draw 3 smaller gaskets
      int q1X = (p1X + p2X) / 2;    int q1Y = (p1Y + p2Y) / 2;
      int q2X = (p1X + p3X) / 2;    int q2Y = (p1Y + p3Y) / 2;
      int q3X = (p2X + p3X) / 2;    int q3Y = (p2Y + p3Y) / 2;
      drawGasket(g, lev - 1, p1X, p1Y, q1X, q1Y, q2X, q2Y);
      drawGasket(g, lev - 1, p2X, p2Y, q1X, q1Y, q3X, q3Y);
      drawGasket(g, lev - 1, p3X, p3Y, q2X, q2Y, q3X, q3Y);
    } // if
} // drawGasket()

/**
     * paint() is the public method that handles drawing of the boxes 
     * @param g is a reference to the current Graphics object
     */
    public void paint(Graphics g) {
        drawGasket(g, level, 10, 10, 390, 10,200,390);
    } // paint()

public static void main(String args[]) {
        Triangles b = new Triangles();
        // display code changed to work in ActiveCode
        HtmlImageUtil.show(b,400,400);
    }
} // Triangles

🔗

You have attempted 1 of 3 activities on this page.

🔗

Prev Top Next