Section 8.8 Priority Queues with Binary Heaps Example
As mentioned before we can use binary heaps in order to design a priority queue, according to our preference, using a min or max heap would allow us to construct a tree in such a way that the children are always larger or smaller than the parent, respectively. In the example in this section we will be using min heap structure. That way the smallest element will always be at the root, that is the goal of using a heap for a priority queue, since this will allow for swift removal of the element with utmost priority. When inserting new elements into the heap it is important to maintain the priority structure, therefore every time we insert a new element, not only do we insert it in such a way to fill out the tree from left to right, but we also make sure that every parent node is smaller then the child node that we inserted. This way if the inserted node is the smallest node in the tree it will bubble up to the root and push everything else lower into the heap. Deletion of the items is also important, since we know that the element with utmost priority is always at the root we can simply remove the root and replace it with the righmost leaf. However now our priority structure is broken, we can fix this by swaping it with the lesser of its children, then the structure will be correct agian. This structure allows for effective maintenance of the priority of the items and greatly improves the efficiency of our priority queue.
Before we begin with the implementation of Binary Heaps, let us review a real life example of one of the things: Priority Queues. Let us consider a priority queue of homework. If we were trying to decide which homework project to complete, it would make sense to organize the order of doing any specific project based on the deadline of that homework. Let us say you were assigned homeworks in the following order and you are told the deadlines for those homeworks: 3, 10, 5, 8, 7, 2 days respectively. You can observe the insertion of these homeworks into our priority queue in Figure 8.8.1.
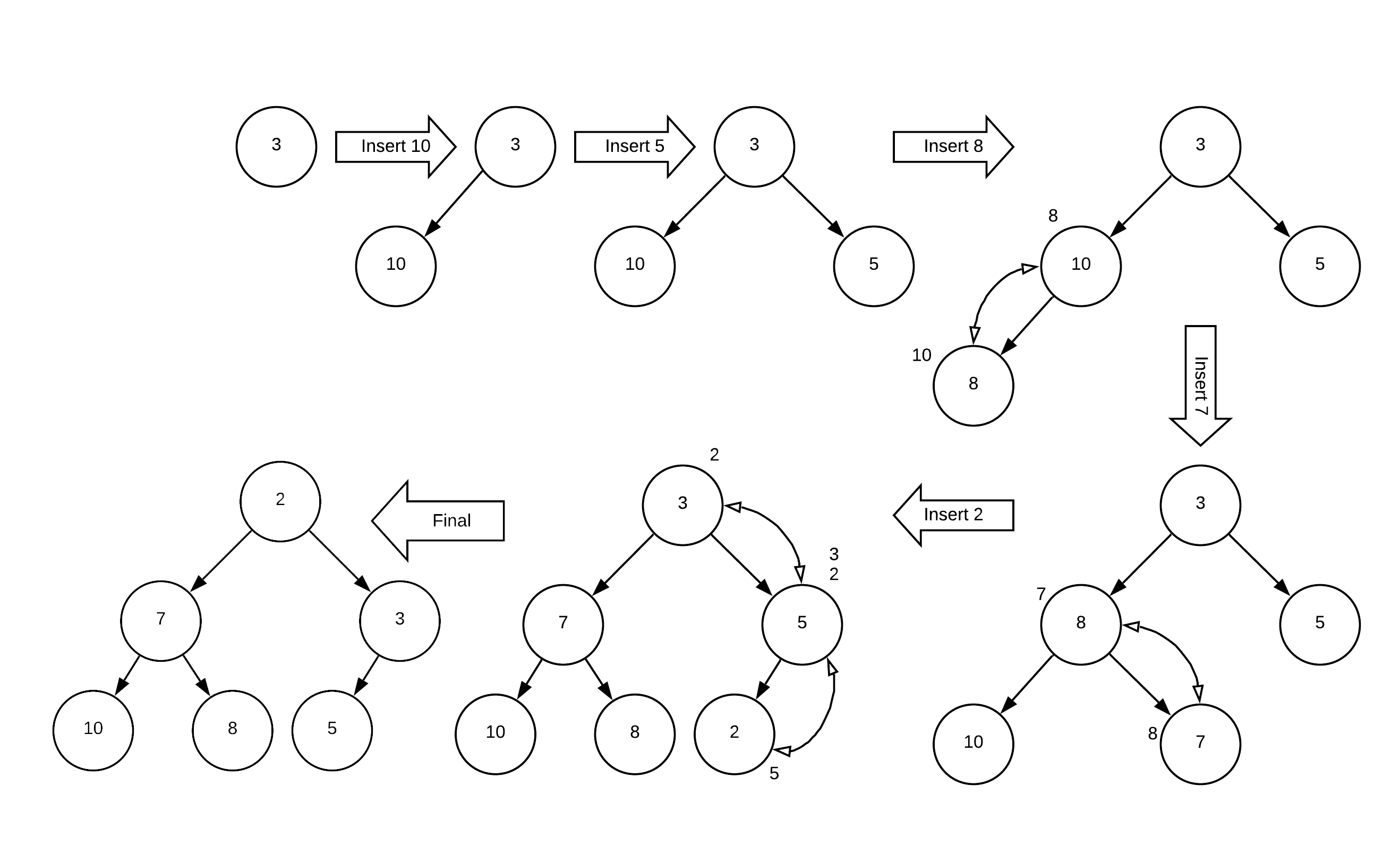
A sequence of diagrams depicting the insertion process into a priority queue represented by a binary tree. Starting with a single node labeled ’3’, the first diagram shows ’Insert 10’, leading to a new node ’10’ added as a child. The next step ’Insert 5’ adds a new node ’5’, followed by ’Insert 8’ which adds node ’8’. Another step shows ’Insert 7’ with a node ’7’ being added, and the sequence progresses with each insertion maintaining the binary tree structure. The diagrams show the dynamic reordering of nodes to maintain the priority queue property, with the final structure at the bottom left displaying a balanced binary tree with node ’2’ at the top, leading to nodes ’3’ and ’7’, which branch out to further nodes ’10’, ’8’, ’5’, and ’2’. Arrows indicate the insertion order and the adjustments within the tree.
Now that we have the priority queue of which homeworks we need to do in the order. Let us start by doing the homework with 2 day deadline. We would remove it from the root and put the left most leaf in its place and than rearange the heap back to the proper state, as shown in Figure 8.8.2.
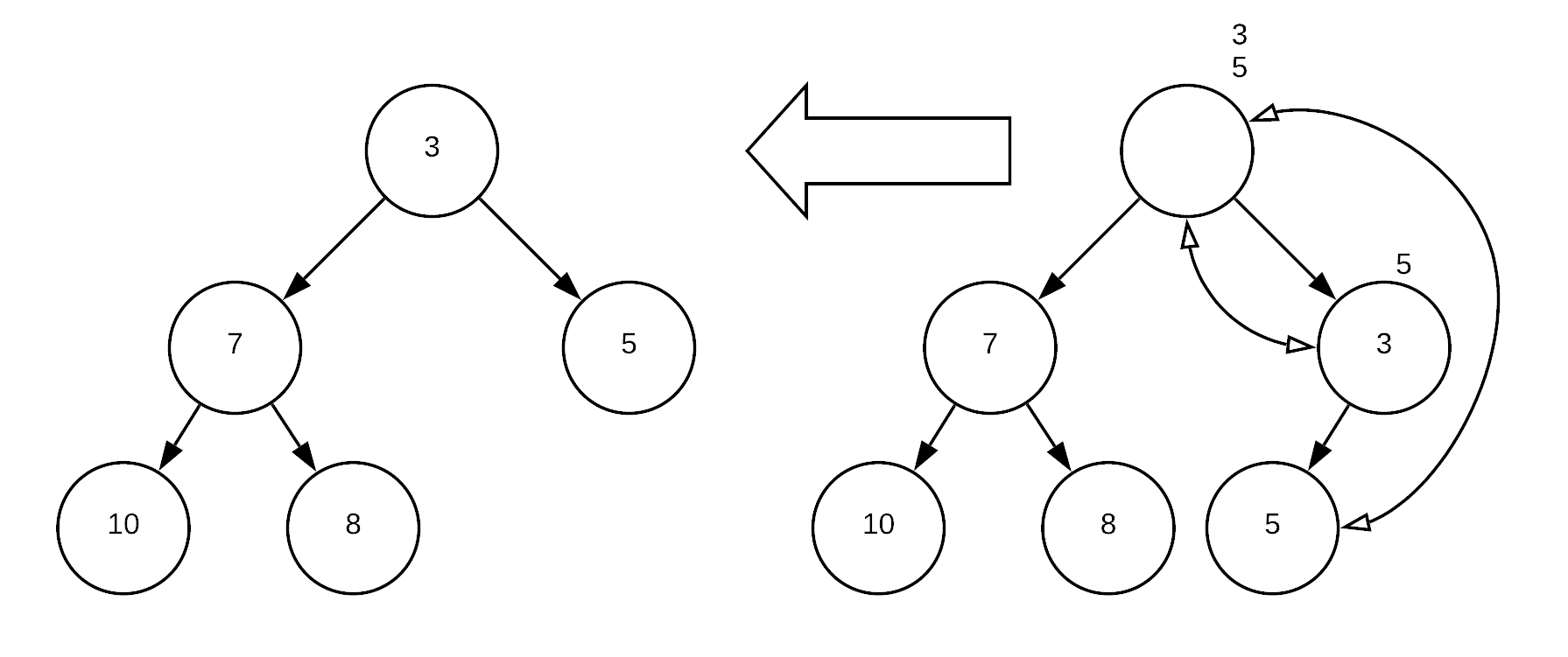
Two diagrams showing the process of removing the root from a binary heap that represents a priority queue. The first diagram on the left shows a binary tree with the root node ’3’, which has two children: ’7’ on the left with its own children ’10’ and ’8’, and ’5’ on the right. An arrow points from this tree to the second diagram on the right, indicating the removal of the root node. The second diagram shows the tree after the root has been removed and the heap has been restructured: the node ’5’ has been moved to the root position, with ’7’ as its left child and ’3’ as its right child, maintaining the heap property. The nodes ’10’ and ’8’ remain as children of ’7’. The tree restructuring is shown with curved arrows indicating the new parent-child relationships.
As we continue to complete the homework with the closest deadline we will continue to remove the homeworks in the demostrated fashion until we are done.
You have attempted of activities on this page.
