Section 9.5 An Adjacency List
A more space-efficient way to implement a sparsely connected graph is to use an adjacency list. In an adjacency list implementation we keep a master list of all the vertices in the Graph object and then each vertex object in the graph maintains a list of the other vertices that it is connected to. In our implementation of the
Vertex class we will use a dictionary rather than a list where the dictionary keys are the vertices, and the values are the weights. Figure 9.5.1 illustrates the adjacency list representation for the graph in Figure 9.2.1.
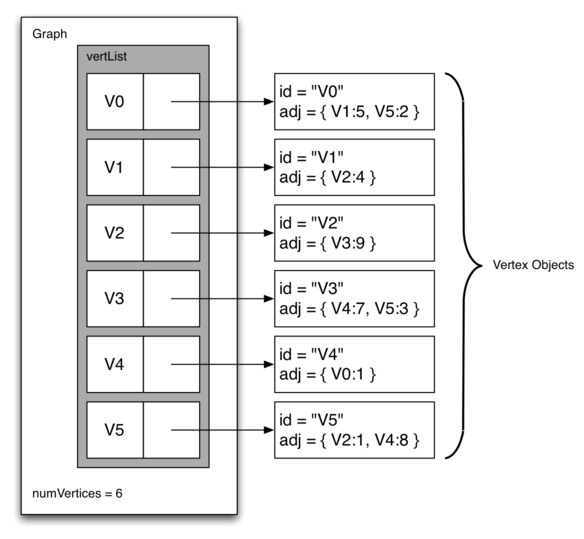
Image displaying an adjacency list representation of a graph. The illustration shows a table labeled ’Graph’ with a column ’vertList’ containing vertices ’V0’ through ’V5’. Next to each vertex is a corresponding vertex object, with ’id’ representing the vertex ID and ’adj’ listing its adjacent vertices along with the edge weights. For example, ’V0’ has an adjacent vertex ’V1’ with a weight of 5 and ’V5’ with a weight of 2, ’V1’ is adjacent to ’V2’ with a weight of 4, and so on. The bottom of the table states ’numVertices = 6’, indicating the total number of vertices in the graph.
The advantage of the adjacency list implementation is that it allows us to compactly represent a sparse graph. The adjacency list also allows us to easily find all the links that are directly connected to a particular vertex.
You have attempted of activities on this page.
