Section 8.20 Discussion Questions
-
Draw the tree structure resulting from the following set of tree function calls:
>>> r = BinaryTree(3) >>> insertLeft(r,4) [3, [4, [], []], []] >>> insertLeft(r,5) [3, [5, [4, [], []], []], []] >>> insertRight(r,6) [3, [5, [4, [], []], []], [6, [], []]] >>> insertRight(r,7) [3, [5, [4, [], []], []], [7, [], [6, [], []]]] >>> setRootVal(r,9) >>> insertLeft(r,11) [9, [11, [5, [4, [], []], []], []], [7, [], [6, [], []]]]
-
Trace the algorithm for creating an expression tree for the expression \((4 * 8) / 6 - 3\text{.}\)
-
Consider the following array of integers: [1,2,3,4,5,6,7,8,9,10]. Show the binary search tree resulting from inserting the integers in the array.
-
Consider the following array of integers: [10,9,8,7,6,5,4,3,2,1]. Show the binary search tree resulting from inserting the integers in the array.
-
Generate a random array of integers. Show the binary heap tree resulting from inserting the integers on the array one at a time.
-
Using the array from the previous question, show the binary heap tree resulting from using the array as a parameter to the
buildHeapmethod. Show both the tree and array form. -
Draw the binary search tree that results from inserting the following keys in the order given: 68,88,61,89,94,50,4,76,66, and 82.
-
Generate a random array of integers. Draw the binary search tree resulting from inserting the integers on the array.
-
Consider the following array of integers: [1,2,3,4,5,6,7,8,9,10]. Show the binary heap resulting from inserting the integers one at a time.
-
Consider the following array of integers: [10,9,8,7,6,5,4,3,2,1]. Show the binary heap resulting from inserting the integers one at a time.
-
Consider the two different techniques we used for implementing traversals of a binary tree. Why must we check before the call to
preorderwhen implementing as a method, whereas we could check inside the call when implementing as a function? -
Show the function calls needed to build the binary tree in Figure 8.20.1.
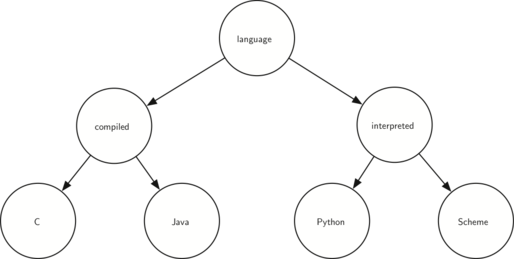 A tree whose root node is language. The language node has two children: compiled and interpreted. The compiled node has two children: C and Java. The interpreted node has two children: Python and Scheme.
A tree whose root node is language. The language node has two children: compiled and interpreted. The compiled node has two children: C and Java. The interpreted node has two children: Python and Scheme.Figure 8.20.1. Tree of Programming Languages -
Given the tree in Figure 8.20.2, perform the appropriate rotations to bring it back into balance.
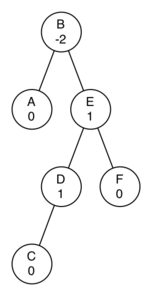 A tree whose root node is B with a balance factor of -2. B has two children: A with a balance factor of 0 and E with a balanace factor of 1. A has no children. E has two children: D with a balance factor of 1 and F with a balance factor of 0. D has only a left child: C with balance factor 0. F has no children.
A tree whose root node is B with a balance factor of -2. B has two children: A with a balance factor of 0 and E with a balanace factor of 1. A has no children. E has two children: D with a balance factor of 1 and F with a balance factor of 0. D has only a left child: C with balance factor 0. F has no children.Figure 8.20.2. Out of Balance Tree -
Using Figure 8.20.3 as a starting point, derive the equation that gives the updated balance factor for node D.
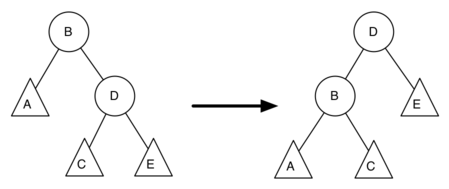 Image illustrating a left rotation in a binary tree. The diagram consists of two stages: the initial tree structure and the resulting tree after the rotation. In the initial tree, node "B" is the root, with node "A" as its left child and node "D" as its right child. Node "D" has two subtrees, "C" as its left child and "E" as its right child. After the left rotation, node "D" becomes the new root, with node "B" as its left child and node "E" as its right child. Node "B" retains "A" as its left child and "C" as its right child. The arrow between the two stages indicates the direction of the rotation. This figure demonstrates the rebalancing operation in a binary tree by performing a left rotation.
Image illustrating a left rotation in a binary tree. The diagram consists of two stages: the initial tree structure and the resulting tree after the rotation. In the initial tree, node "B" is the root, with node "A" as its left child and node "D" as its right child. Node "D" has two subtrees, "C" as its left child and "E" as its right child. After the left rotation, node "D" becomes the new root, with node "B" as its left child and node "E" as its right child. Node "B" retains "A" as its left child and "C" as its right child. The arrow between the two stages indicates the direction of the rotation. This figure demonstrates the rebalancing operation in a binary tree by performing a left rotation.Figure 8.20.3. Compute Updated Balance Factor
You have attempted of activities on this page.
