Section 9.12 Building the Knight’s Tour Graph
To represent the knight’s tour problem as a graph we will use the following two ideas: Each square on the chessboard can be represented as a node in the graph. Each legal move by the knight can be represented as an edge in the graph. Figure 9.12.1 illustrates the legal moves by a knight and the corresponding edges in a graph.
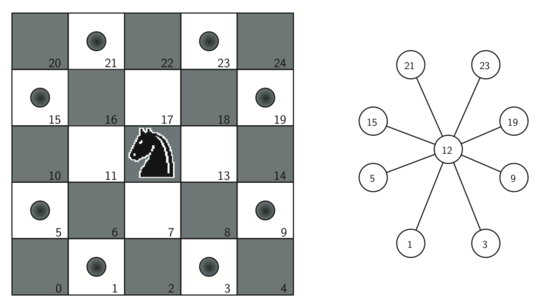
Image depicting the legal moves for a knight on a chessboard and the corresponding graph. On the left, there is a 5x5 section of a chessboard with numbered squares from 1 to 25. The knight is placed on square 12, with its legal moves indicated by gray dots on squares 5, 9, 15, 19, 21, and 23. On the right, a graph illustrates the knight’s moves as a network of connected nodes. The central node, labeled ’12’, represents the knight’s position, and it is connected to nodes labeled ’5’, ’9’, ’15’, ’19’, ’21’, and ’23’, which correspond to the potential moves available to the knight from its current position.
To build the full graph for an n-by-n board we can use the C++ function shown in Listing 9.12.2. The
knightGraph function makes one pass over the entire board. At each square on the board the knightGraph function calls a helper, genLegalMoves, to create a list of legal moves for that position on the board. All legal moves are then converted into edges in the graph. Another helper function coordToNum converts a location on the board in terms of a row and a column into a linear vertex number similar to the vertex numbers shown in Figure 9.12.1.
Graph knightGraph(int bdSize) {
Graph ktGraph(false);
for (int row = 0; row < bdSize; row++) {
for (int col = 0; col < bdSize; col++) {
int nodeId = coordToNum(row, col, bdSize);
vector<int> newPositions = genLegalMoves(nodeId, bdSize);
for (int i = 0; i < newPositions.size(); i++) {
int newId = newPositions[i];
ktGraph.addEdge(nodeId, newId);
}
}
}
return ktGraph;
}
The
genLegalMoves function (Listing 9.12.3) takes the position of the knight on the board and generates each of the eight possible moves. The legalCoord helper function (Listing 9.12.3) makes sure that a particular move that is generated is still on the board.
int coordToNum(int x, int y, int bdSize) {
// Takes the x y position and returns the id from 0 to (bdSize*2)-1
int id = 0;
id += y * bdSize;
id += x;
return id;
}
pair<int, int> numToCoord(int id, int bdSize) {
int x, y;
x = id % bdSize;
y = (id - x) / bdSize;
return make_pair(x, y);
}
bool legalCoord(int x, int bdSize) {
if (x >= 0 && x < bdSize) {
return true;
} else {
return false;
}
}
vector<int> genLegalMoves(int id, int bdSize) {
pair<int, int> coords = numToCoord(id, bdSize);
int x = coords.first;
int y = coords.second;
vector<int> newMoves;
vector<pair<int, int>> myVec = {
{-1, -2}, {-1, 2}, {-2, -1}, {-2, 1}, {1, -2}, {1, 2}, {2, -1}, {2, 1}};
for (unsigned int i = 0; i < myVec.size(); i++) {
int newX = x + myVec[i].first;
int newY = y + myVec[i].second;
if (legalCoord(newX, bdSize) && legalCoord(newY, bdSize)) {
newMoves.push_back(coordToNum(newX, newY, bdSize));
}
}
return newMoves;
}
Figure 9.12.4 shows the complete graph of possible moves on an eight-by-eight board. There are exactly 336 edges in the graph. Notice that the vertices corresponding to the edges of the board have fewer connections (legal moves) than the vertices in the middle of the board. Once again we can see how sparse the graph is. If the graph was fully connected there would be 4,096 edges. Since there are only 336 edges, the adjacency matrix would be only 8.2 percent full.

Complex graph showing all legal moves for a knight on an 8 x 8 chessboard, visualized as a network. The nodes are arranged in a grid pattern, numbered from 0 to 63, corresponding to the squares of a chessboard. The lines connecting the nodes represent the knight’s potential moves, with each node being connected to others that a knight could reach in a single move based on the rules of chess. The myriad of crisscrossing lines create an intricate web, illustrating the complexity of the knight’s movement possibilities across the entire board.
The full implementation of this is shown in Listing 9.12.5. In the main function, we traverse using our previously created breadth-first search between two locations. In the next chapter, we will implement a different algorithm called a
depth first search (DFS) to solve our knight’s tour problem.
You have attempted of activities on this page.
