Appendix F Hints and Solutions to Selected Exercises
For the most part, solutions are provided here for odd-numbered exercises.
1 Set Theory
1.1 Set Notation and Relations
1.1.3 Exercises for Section 1.1
1.1.3.3.
1.1.3.5.
1.1.3.7.
1.2 Basic Set Operations
1.2.4 Exercises
1.2.4.1.
Answer.
-
\(\displaystyle \{2,3\}\)
-
\(\displaystyle \{0,2,3\}\)
-
\(\displaystyle \{0,2,3\}\)
-
\(\displaystyle \{0,1,2,3,5,9\}\)
-
\(\displaystyle \{0\}\)
-
\(\displaystyle \emptyset\)
-
\(\displaystyle \{ 1,4,5,6,7,8,9\}\)
-
\(\displaystyle \{0,2,3,4,6,7,8\}\)
-
\(\displaystyle \emptyset\)
-
\(\displaystyle \{0\}\)
1.2.4.3.
1.2.4.5.
1.2.4.7.
1.3 Cartesian Products and Power Sets
1.3.4 Exercises
1.3.4.1.
Answer.
-
\(\displaystyle \{(0, 2), (0, 3), (2, 2), (2, 3), (3, 2), (3, 3)\}\)
-
\(\displaystyle \{(2, 0), (2, 2), (2, 3), (3, 0), (3, 2), (3, 3)\}\)
-
\(\displaystyle \{(0, 2, 1), (0, 2, 4), (0, 3, 1), (0, 3, 4), (2, 2, 1), (2, 2, 4),\\ (2, 3, 1), (2, 3, 4), (3, 2, 1), (3, 2, 4), (3, 3, 1), (3, 3, 4)\}\)
-
\(\displaystyle \emptyset\)
-
\(\displaystyle \{(0, 1), (0, 4), (2, 1), (2, 4), (3, 1), (3, 4)\}\)
-
\(\displaystyle \{(2, 2), (2, 3), (3, 2), (3, 3)\}\)
-
\(\displaystyle \{(2, 2, 2), (2, 2, 3), (2, 3, 2), (2, 3, 3), (3, 2, 2), (3, 2, 3), (3, 3, 2), (3, 3, 3)\}\)
-
\(\displaystyle \{(2, \emptyset ), (2, \{2\}), (2, \{3\}), (2, \{2, 3\}), (3, \emptyset ), (3, \{2\}), (3, \{3\}), (3, \{2, 3\})\}\)
1.3.4.3.
1.3.4.5.
1.3.4.7.
1.3.4.9.
1.4 Binary Representation of Positive Integers
1.4.3 Exercises
1.4.3.1.
1.4.3.3.
1.4.3.5.
Answer.
There is a bit for each power of 2 up to the largest one needed to represent an integer, and you start counting with the zeroth power. For example, 2017 is between \(2^{10}=1024\) and \(2^{11}=2048\text{,}\) and so the largest power needed is \(2^{10}\text{.}\) Therefore there are \(11\) bits in binary 2017.
1.4.3.7.
1.5 Summation Notation and Generalizations
1.5.3 Exercises
1.5.3.1.
1.5.3.3.
Answer.
-
\(\displaystyle \frac{1}{1 (1+1)}+\frac{1}{2 (2+1)}+\frac{1}{3 (3+1)}+\cdots +\frac{1}{n(n+1)}=\frac{n}{n+1}\)
-
\(\displaystyle \frac{1}{1(2)}+\frac{1}{2(3)}+\frac{1}{3(4)}=\frac{1}{2}+\frac{1}{6}+\frac{1}{12}=\frac{3}{4}=\frac{3}{3+1}\)
-
\(1+2^3+3^3+\cdots +n^3=\left(\frac{1}{4}\right)n^2(n+1)^2\) \(\quad 1+8+27=36 = \left(\frac{1}{4}\right)(3)^2(3+1)^2\)
1.5.3.5.
1.5.3.7.
1.5.3.9.
2 Combinatorics
2.1 Basic Counting Techniques - The Rule of Products
2.1.3 Exercises
2.1.3.1.
2.1.3.3.
2.1.3.5.
2.1.3.7.
2.1.3.9.
2.1.3.11.
2.1.3.13.
2.1.3.15.
2.1.3.17.
Answer.
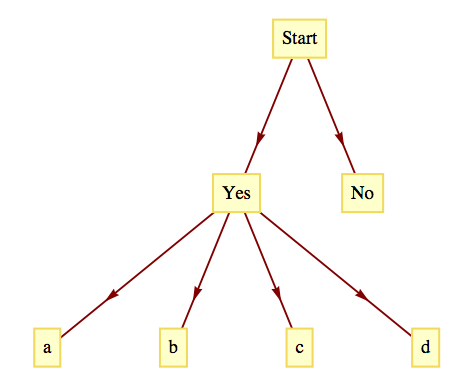
solution to exercise 17a of section 2.1. From a start node, there are two branches. The first branch, labeled yes, has four branches coming from it, one for each of the possible follow-up responses. The second branch from start is an end branch labeled no.
2.1.3.19.
2.2 Permutations
2.2.2 Exercises
2.2.2.1.
2.2.2.3.
2.2.2.5.
2.2.2.7.
2.2.2.9.
2.2.2.11.
2.3 Partitions of Sets and the Law of Addition
2.3.3 Exercises
2.3.3.1.
2.3.3.3.
2.3.3.5.
2.3.3.7.
2.3.3.9.
Solution.
We assume that \(\lvert A_1 \cup A_2 \rvert = \lvert A_1 \rvert +\lvert A_2\rvert -\lvert A_1\cap A_2\rvert \text{.}\)
\begin{equation*}
\begin{split}
\lvert A_1 \cup A_2\cup A_3 \rvert & =\lvert (A_1\cup A_2) \cup A_3 \rvert \quad Why?\\
& = \lvert A_1\cup A_2\rvert +\lvert A_3 \rvert -\lvert (A_1\cup A_2)\cap A_3\rvert \quad Why? \\
& =\lvert (A_1\cup A_2\rvert +\lvert A_3\rvert -\lvert (A_1\cap A_3)\cup (A_2\cap A_3)\rvert \quad Why?\\
& =\lvert A_1\rvert +\lvert A_2\rvert -\lvert A_1\cap A_2\rvert +\lvert A_3\rvert \\
& \quad -(\lvert A_1\cap A_3\rvert +\lvert A_2\cap A_3\rvert -\lvert (A_1\cap A_3)\cap (A_2\cap A_3)\rvert\quad Why?\\
& =\lvert A_1\rvert +\lvert A_2\rvert +\lvert A_3\rvert -\lvert A_1\cap A_2\rvert -\lvert A_1\cap A_3\rvert\\
& \quad -\lvert A_2\cap A_3\rvert +\lvert A_1\cap A_2\cap A_3\rvert \quad Why?
\end{split}
\end{equation*}
The law for four sets is
\begin{equation*}
\begin{split}
\lvert A_1\cup A_2\cup A_3\cup A_4\rvert & =\lvert A_1\rvert +\lvert A_2\rvert +\lvert A_3\rvert +\lvert A_4\rvert\\
& \quad -\lvert A_1\cap A_2\rvert -\lvert A_1\cap A_3\rvert -\lvert A_1\cap A_4\rvert \\
& \quad \quad -\lvert A_2\cap A_3\rvert -\lvert A_2\cap A_4\rvert -\lvert A_3\cap A_4\rvert \\
& \quad +\lvert A_1\cap A_2\cap A_3\rvert +\lvert A_1\cap A_2\cap A_4\rvert \\
& \quad \quad +\lvert A_1\cap A_3\cap A_4\rvert +\lvert A_2\cap A_3\cap A_4\rvert \\
& \quad -\lvert A_1\cap A_2\cap A_3\cap A_4\rvert
\end{split}
\end{equation*}
Derivation:
\begin{equation*}
\begin{split}
\lvert A_1\cup A_2\cup A_3\cup A_4\rvert & = \lvert (A_1\cup A_2\cup A_3)\cup A_4\rvert \\
& = \lvert (A_1\cup A_2\cup A_3\rvert +\lvert A_4\rvert -\lvert (A_1\cup A_2\cup A_3)\cap A_4\rvert\\
& = \lvert (A_1\cup A_2\cup A_3\rvert +\lvert A_4\rvert \\
& \quad -\lvert (A_1\cap A_4)\cup (A_2\cap A_4)\cup (A_3\cap A_4)\rvert \\
& = \lvert A_1\rvert +\lvert A_2\rvert +\lvert A_3\rvert -\lvert A_1\cap A_2\rvert -\lvert A_1\cap A_3\rvert \\
& \quad -\lvert A_2\cap A_3\rvert +\lvert A_1\cap A_2\cap A_3\rvert +\lvert A_4\rvert -\lvert A_1\cap A_4\rvert \\
& \quad+\lvert A_2\cap A_4\rvert +\lvert A_3\cap A_4\rvert -\lvert (A_1\cap A_4)\cap (A_2\cap A_4)\rvert \\
& \quad -\lvert (A_1\cap A_4)\cap (A_3\cap A_4)\rvert -\lvert (A_2\cap A_4)\cap (A_3\cap A_4)\rvert \\
& \quad +\lvert (A_1\cap A_4)\cap (A_2\cap A_4)\cap (A_3\cap A_4)\rvert \\
& =\lvert A_1\rvert +\lvert A_2\rvert +\lvert A_3\rvert +\lvert A_4\rvert -\lvert A_1\cap A_2\rvert -\lvert A_1\cap A_3\rvert \\
& \quad -\lvert A_2\cap A_3\rvert -\lvert A_1\cap A_4\rvert -\lvert A_2\cap A_4\rvert \quad -\lvert A_3\cap A_4\rvert \\
& \quad +\lvert A_1\cap A_2\cap A_3\rvert +\lvert A_1\cap A_2\cap A_4\rvert \\
& \quad +\lvert A_1\cap A_3\cap A_4\rvert +\lvert A_2\cap A_3\cap A_4\rvert \\
& \quad -\lvert A_1\cap A_2 \cap A_3\cap A_4\rvert
\end{split}
\end{equation*}
2.3.3.11.
Answer.
2.4 Combinations and the Binomial Theorem
2.4.4 Exercises
2.4.4.1.
2.4.4.2.
2.4.4.3.
2.4.4.5.
Answer.
Each path can be described as a sequence or R’s and U’s with exactly six of each. The six positions in which R’s could be placed can be selected from the twelve positions in the sequence \(\binom{12}{6} =924\) ways. We can generalize this logic and see that there are \(\binom{m+n}{m}\) paths from \((0,0)\) to \((m,n)\text{.}\)
2.4.4.7.
2.4.4.9.
2.4.4.11.
2.4.4.13.
2.4.4.15.
Answer.
Assume \(\lvert A \rvert =n\text{.}\) If we let \(x=y=1\) in the Binomial Theorem, we obtain \(2^n=\binom{n}{0}+\binom{n}{1}+\cdots +\binom{n}{n}\text{,}\) with the right side of the equality counting all subsets of \(A\) containing \(0, 1, 2, \dots , n\) elements. Hence \(\lvert P(A)\rvert =2^{\lvert A \rvert}\)
2.4.4.17.
3 Logic
3.1 Propositions and Logical Operators
3.1.3 Exercises
3.1.3.1.
3.1.3.3.
Answer.
-
\(2>5\) and 8 is an even integer. False.
-
If \(2\leqslant 5\) then 8 is an even integer. True.
-
If \(2\leqslant 5\) and 8 is an even integer then 11 is a prime number. True.
-
If \(2\leqslant 5\) then either 8 is an even integer or 11 is not a prime number. True.
-
If \(2\leqslant 5\) then either 8 is an odd integer or 11 is not a prime number. False.
-
If 8 is not an even integer then \(2>5\text{.}\) True.
3.1.3.5.
3.2 Truth Tables and Propositions Generated by a Set
3.2.4 Exercises
3.2.4.1.
Answer.
-
\(\displaystyle \begin{array}{cc} p & p\lor p \\ \hline 0 & 0 \\ 1 & 1 \\ \end{array}\)
-
\(\displaystyle \begin{array}{ccc} p & \neg p & p\land (\neg p) \\ \hline 0 & 1 & 0 \\ 1 & 0 & 0 \\ \end{array}\)
-
\(\displaystyle \begin{array}{ccc} p & \neg p & p\lor (\neg p) \\ \hline 0 & 1 & 1 \\ 1 & 0 & 1 \\ \end{array}\)
-
\(\displaystyle \begin{array}{cc} p & p\land p \\ \hline 0 & 0 \\ 1 & 1 \\ \end{array}\)
3.2.4.3.
3.2.4.5.
3.3 Equivalence and Implication
3.3.5 Exercises
3.3.5.1.
3.3.5.3.
Solution.
No. In symbolic form the question is: Is \((p\to q)\Leftrightarrow (q\to p)\text{?}\) \(\begin{array}{ccccc}
p & q & p\to q & q\to p & (p\to q)\leftrightarrow (q\to p) \\
\hline
0 & 0 & 1 & 1 & 1\\
0 & 1 & 1 & 0 & 0\\
1 & 0 & 0 & 1 & 0 \\
1 & 1 & 1 & 1 & 1 \\
\end{array}\)
This table indicates that an implication is not always equivalent to its converse.
3.3.5.5.
3.3.5.7.
3.3.5.9.
Solution.
Yes. In symbolic form the question is whether, if we have a conditional proposition \(p \to q\text{,}\) is \((q\to p)\Leftrightarrow (\neg p\to \neg q)\text{?}\)
\(\begin{array}{ccccc}
p & q & q\to p & \neg p\to \neg q & (q \to p)\leftrightarrow (\neg p\to \neg q) \\
\hline
0 & 0 & 1 & 1 & 1\\
0 & 1 & 0 & 0 & 1\\
1 & 0 & 1 & 1 & 1 \\
1 & 1 & 1 & 1 & 1 \\
\end{array}\)
This table indicates that an converse is always equivalent to the inverse.
3.4 The Laws of Logic
3.4.2 Exercises
3.4.2.1.
Answer.
Let \(s=\textrm{I will study}\text{,}\)\(t=\textrm{I will learn.}\) The argument is: \(((s\to t)\land (\neg t))\to (\neg s) ,\) call the argument \(a\text{.}\)
\begin{equation*}
\begin{array}{ccccc}
s\text{ } & t\text{ } & s\to t\text{ } & (s\to t)\land (\neg t)\text{ } & a \\
\hline
0\text{ } & 0\text{ } & 1\text{ } & 1\text{ } & 1 \\
0\text{ } & 1\text{ } & 1\text{ } & 0\text{ } & 1 \\
1\text{ } & 0\text{ } & 0\text{ } & 0\text{ } & 1 \\
1\text{ } & 1\text{ } & 1\text{ } & 0\text{ } & 1 \\
\end{array}\text{.}
\end{equation*}
Since \(a\) is a tautology, the argument is valid.
3.4.2.3.
3.5 Mathematical Systems and Proofs
3.5.4 Exercises
3.5.4.1.
Answer.
-
\begin{equation*} \begin{array}{cccc} p & q & (p\lor q)\land \neg q & ((p\lor q)\land \neg q)\to p \\ 0 & 0 & 0 & 1 \\ 0 & 1 & 0 & 1 \\ 1 & 0 & 1 & 1 \\ 1 & 1 & 0 & 1 \\ \end{array} \end{equation*}
-
\begin{equation*} \begin{array}{ccccc} p & q & (p\to q)\land \neg q & \neg p & ((p\to q)\land (\neg q))\rightarrow \neg p \\ 0 & 0 & 1 & 1 & 1 \\ 0 & 1 & 0 & 1 & 1 \\ 1 & 0 & 0 & 0 & 1 \\ 1 & 1 & 0 & 0 & 1 \\ \end{array} \end{equation*}
3.5.4.3.
Answer.
-
Direct proof:
-
\(\displaystyle d\to (a\lor c)\)
-
\(\displaystyle d\)
-
\(\displaystyle a\lor c\)
-
\(\displaystyle a\to b\)
-
\(\displaystyle \neg a \lor b\)
-
\(\displaystyle c\to b\)
-
\(\displaystyle \neg c\lor b\)
-
\(\displaystyle (\neg a\lor b)\land (\neg c\lor b)\)
-
\(\displaystyle (\neg a\land \neg c) \lor b\)
-
\(\displaystyle \neg (a\lor c)\lor b\)
Indirect proof:-
\(\neg b\quad \) Negated conclusion
-
\(a\to b\quad \) Premise
-
\(\neg a\quad \) Indirect Reasoning (1), (2)
-
\(c\to b\quad \) Premise
-
\(\neg c\quad \) Indirect Reasoning (1), (4)
-
\((\neg a\land \neg c)\quad \) Conjunctive (3), (5)
-
\(\neg (a\lor c)\quad \) DeMorgan’s law (6)
-
\(d\to (a\lor c)\quad \) Premise
-
\(\neg d\quad \) Indirect Reasoning (7), (8)
-
\(d\quad \) Premise
-
-
Direct proof:
-
\(\displaystyle (p\to q)\land (r\to s)\)
-
\(\displaystyle p\to q\)
-
\(\displaystyle (p\to t)\land (s\to u)\)
-
\(\displaystyle q\to t\)
-
\(\displaystyle p\to t\)
-
\(\displaystyle r\to s\)
-
\(\displaystyle s\to u\)
-
\(\displaystyle r\to u\)
-
\(\displaystyle p\to r\)
-
\(\displaystyle p\to u\)
-
\(\displaystyle \neg (t\land u)\to \neg p\)
-
\(\displaystyle \neg (t\land u)\)
Indirect proof:-
\(\displaystyle p\)
-
\(\displaystyle p\to q\)
-
\(\displaystyle q\)
-
\(\displaystyle q\to t\)
-
\(\displaystyle t\)
-
\(\displaystyle \neg (t\land u)\)
-
\(\displaystyle \neg t\lor \neg u\)
-
\(\displaystyle \neg u\)
-
\(\displaystyle s\to u\)
-
\(\displaystyle \neg s\)
-
\(\displaystyle r\to s\)
-
\(\displaystyle \neg r\)
-
\(\displaystyle p\to r\)
-
\(\displaystyle r\)
-
-
Direct proof:
-
\(\neg s\lor p\quad \) Premise
-
\(s\quad \) Added premise (conditional conclusion)
-
\(\neg (\neg s)\quad \) Involution (2)
-
\(p \quad \) Disjunctive simplification (1), (3)
-
\(p\to (q\to r)\quad \) Premise
-
\(q\to r\quad \) Detachment (4), (5)
-
\(q \quad\) Premise
Indirect proof:-
\(\neg (s\to r)\quad \) Negated conclusion
-
\(\neg (\neg s\lor r)\quad \) Conditional equivalence (1)
-
\(s\land \neg r\quad \) DeMorgan (2)
-
\(s\quad\) Conjunctive simplification (3)
-
\(\neg s\lor p\quad \) Premise
-
\(s\to p\quad\) Conditional equivalence (5)
-
\(p \quad\) Detachment (4), (6)
-
\(p\to (q\to r)\quad\) Premise
-
\(q\to r \quad\) Detachment (7), (8)
-
\(q\quad \) Premise
-
\(r\quad\) Detachment (9), (10)
-
\(\neg r \quad\) Conjunctive simplification (3)
-
-
Direct proof:
-
\(\displaystyle p\to q\)
-
\(\displaystyle q\to r\)
-
\(\displaystyle p\to r\)
-
\(\displaystyle p\lor r\)
-
\(\displaystyle \neg p\lor r\)
-
\(\displaystyle (p\lor r)\land (\neg p\lor r)\)
-
\(\displaystyle (p\land \neg p)\lor r\)
-
\(\displaystyle 0\lor r\)
Indirect proof:-
\(\neg r\) Negated conclusion
-
\(p\lor r\quad\) Premise
-
\(p\quad\) (1), (2)
-
\(p\to q\quad\) Premise
-
\(q \quad \) Detachment (3), (4)
-
\(q\to r\quad\) Premise
-
\(r \quad \)Detachment (5), (6)
-
3.5.4.5.
Answer.
-
Let \(W\) stand for “Wages will increase,” \(I\) stand for “there will be inflation,” and \(C\) stand for “cost of living will increase.” Therefore the argument is: \(W\to I,\text{ }\neg I\to \neg C,\text{ }W\Rightarrow C\text{.}\) The argument is invalid. The easiest way to see this is through a truth table, which has one case, the seventh, that this false. Let \(x\) be the conjunction of all premises. \(\begin{array}{ccccccccc} W & I & C & \neg I & \neg C & W\to I & \neg I\to \neg C & x & x\to C \\ \hline 0 & 0 & 0 & 1 & 1 & 1 & 1 & 0 & 1 \\ 0 & 0 & 1 & 1 & 0 & 1 & 0 & 0 & 1 \\ 0 & 1 & 0 & 0 & 1 & 1 & 1 & 0 & 1 \\ 0 & 1 & 1 & 0 & 0 & 1 & 1 & 0 & 1 \\ 1 & 0 & 0 & 1 & 1 & 0 & 1 & 0 & 1 \\ 1 & 0 & 1 & 1 & 0 & 0 & 0 & 0 & 1 \\ 1 & 1 & 0 & 0 & 1 & 1 & 1 & 1 & 0 \\ 1 & 1 & 1 & 0 & 0 & 1 & 1 & 1 & 1 \\ \end{array}\)
-
Let \(r\) stand for “the races are fixed,” \(c\) stand for “casinos are crooked,” \(t\) stand for “the tourist trade will decline,” and \(p\) stand for “the police will be happy.” Therefore, the argument is:\begin{equation*} (r\lor c)\to t, t\to p, \neg p\to \neg r\text{.} \end{equation*}The argument is valid. Proof:
-
\(t\to p\quad \) Premise
-
\(\neg p\quad \) Premise
-
\(\neg t\quad \) Indirect Reasoning (1), (2)
-
\((r\lor c)\to t\quad \) Premise
-
\(\neg (r\lor c)\quad \) Indirect Reasoning (3), (4)
-
\((\neg r)\land (\neg c)\quad \) DeMorgan (5)
-
3.5.4.7.
Answer.
\(p_1\to p_k\) and \(p_k\to p_{k+1}\) implies \(p_1\to p_{k+1}\text{.}\) It takes two steps to get to \(p_1\to p_{k+1}\) from \(p_1\to p_k\) This means it takes \(2(100-1)\) steps to get to \(p_1\to p_{100}\) (subtract 1 because \(p_1\to p_2\) is stated as a premise). A final step is needed to apply detachment to imply \(p_{100}\)
3.6 Propositions over a Universe
3.6.3 Exercises
3.6.3.1.
Answer.
-
\(\displaystyle \{\{1\},\{3\},\{1,3\},\emptyset\}\)
-
\(\displaystyle \{\{3\}, \{3,4\}, \{3,2\}, \{2,3,4\}\}\)
-
\(\displaystyle \{\{1\}, \{1,2\}, \{1,3\}, \{1,4\}, \{1,2,3\}, \{1,2,4\}, \{1,3,4\}, \{1,2,3,4\}\}\)
-
\(\displaystyle \{\emptyset, \{2\}, \{3\}, \{4\}, \{2,3\}, \{2,4\}, \{3,4\}\}\)
-
\(\displaystyle \{A\subseteq U:\left| A\right| =2\}\)
3.6.3.3.
3.6.3.5.
3.6.3.7.
3.7 Mathematical Induction
3.7.4 Exercises
3.7.4.1.
Answer.
We wish to prove that \(P(n):1+3+5+\cdots +(2n-1)=n^2\) is true for \(n \geqslant 1\text{.}\) Recall that the \(n\)th odd positive integer is \(2n - 1\text{.}\)
Induction: Assume that for some \(n\geqslant 1\text{,}\) \(P(n)\) is true. Then we infer that \(P(n+1)\) follows:
\begin{equation*}
\begin{split}
1+3+\cdots +(2(n+1)-1) &= (1+3+\cdots +(2n-1) ) +(2(n+1)-1)\\
& =n^2+(2n+1) \quad \textrm{by } P(n) \textrm{ and basic algebra}\\
& =(n+1)^2 \quad \square
\end{split}
\end{equation*}
3.7.4.3.
Answer.
Proof:
-
Basis: We note that the proposition is true when \(n=1\text{:}\) \(\sum_{k=1}^{1} k^2 =1= \frac{1(2)(3)}{6}\text{.}\)
-
Induction: Assume that the proposition is true for some \(n \geq 1\text{.}\) This is the induction hypothesis.\begin{equation*} \begin{split} \sum_{k=1}^{n+1} k^2 &=\sum_{k=1}^n k^2+(n+1)^2\\ &=\frac{n(n+1)(2n+1)}{6}+(n+1)^2 \qquad \textrm{by the induction hypothesis} \\ &=\frac{(n+1)(2n^2+7n+6)}{6}\\ &=\frac{(n+1)(n+2)(2n+3)}{6}\qquad \square \end{split} \end{equation*}Therefore, the truth of the proposition for \(n\) implies the truth of the proposition for \(n+1\text{.}\)
3.7.4.5.
Solution.
Induction: Assume that for some \(n\geqslant 1\text{,}\) the formula is true.
Then:
\begin{equation*}
\begin{split}
\frac{1}{(1\cdot 2)}+\cdots +\frac{1}{n(n+1)} +\frac{1}{(n+1)(n+2)} &=\frac{n}{n+1}+\frac{1}{(n+1)(n+2)}\\
&=\frac{(n+2)n}{(n+1)(n+2)}+\frac{1}{(n+1)(n+2)}\\
&=\frac{(n+1)^2}{(n+1)(n+2)}\\
&=\frac{n+1}{n+2} \quad \square\\
\end{split}
\end{equation*}
3.7.4.7.
Answer.
Let \(A_n\) be the set of strings of zeros and ones of length \(n\) (we assume that \(\lvert A_n \rvert =2^n\) is known). Let \(E_n\) be the set of the “even” strings, and \(E_{n}^{c}=\) the odd strings. The problem is to prove that for \(n\geqslant 1\text{,}\) \(\lvert E_n \rvert =2^{n-1}\text{.}\) Clearly, \(\lvert E_1\rvert =1\text{,}\) and, if for some \(n\geqslant 1, \lvert E_n\rvert =2^{n-1}\text{,}\) it follows that \(\lvert E_{n+1}\rvert =2^n\) by the following reasoning.
We partition \(E_{n+1}\) according to the first bit: \(E_{n+1}=\{1s\mid s \in E_n^c \}\cup \{ 0s \mid s \in E_n\}\)
Since \(\{1s\mid s \in E_n^c\}\) and \(\{0s \mid s \in E_n\}\) are disjoint, we can apply the addition law. Therefore,
\begin{equation*}
\begin{split}
\quad \lvert E_{n+1}\rvert & =\lvert E_n^c \rvert +\lvert E_n \rvert \\
& =2^{n-1}+ (2^n-2^{n-1}) =2^n.\quad \square
\end{split}
\end{equation*}
3.7.4.9.
Solution.
Assume that for \(n\) persons \((n\geqslant 1),\frac{(n-1)n}{2}\) handshakes take place. If one more person enters the room, he or she will shake hands with \(n\) people,
\begin{equation*}
\begin{split}
\frac{(n-1)n}{2}+n & =\frac{n^2-n+2n}{2}\\
&=\frac{n^2+n}{2}=\frac{n(n+1)}{2}\\
&=\frac{((n+1)-1)(n+1)}{2} \square
\end{split}
\end{equation*}
Also, for \(n=1\text{,}\) there are no handshakes, which matches the conjectured formula:
\begin{equation*}
\frac{(1-1)(1)}{2}=0 \quad \square.
\end{equation*}
3.7.4.11.
Solution.
Basis: \(a_1 + a_2 + a_3\) may be evaluated only two ways. Since + is associative, \((a_1 + a_2) + a_3 = a_1 + (a_2 + a_3)\text{.}\) Hence, \(p(3)\) is true.
Induction: Assume that for some \(n\geq 3\text{,}\) \(p(3), p(4), \dots , p(n)\) are all true. Now consider the sum \(a_1 + a_2 + \cdots + a_n + a_{n+1}\text{.}\) Any of the \(n\) additions in this expression can be applied last. If the \(j\)th addition is applied last, we have \(c_j=(a_1+a_2+\cdots +a_j)+(a_{j+1}+\cdots +a_{n+1})\text{.}\) No matter how the expression to the left and right of the \(j^{\text{th}}\) addition are evaluated, the result will always be the same by the induction hypothesis, specifically \(p(j)\) and \(p(n+1-j)\text{.}\) We now can prove that \(c_1=c_2=\cdots =c_n\text{.}\) If \(i < j\text{,}\)
\begin{equation*}
\begin{split}
c_i &=(a_1+a_2+\cdots +a_i)+(a_{i+1}+\cdots +a_{n+1})\\
&=(a_1+a_2+\cdots +a_i)+(a_{i+1}+\cdots +a_j)+(a_{j+1}+\cdots +a_{n+1})\\
&=((a_1+a_2+\cdots +a_i)+(a_{i+1}+\cdots +a_j))+(a_{j+1}+\cdots +a_{n+1})\\
&=(a_1+a_2+\cdots +a_j)+(a_{j+1}+\cdots +a_{n+1})\\
&=c_j \quad\quad \square
\end{split}
\end{equation*}
3.7.4.12.
3.7.4.13.
Solution.
For \(m\geqslant 1\text{,}\) let \(p(m)\textrm{ be } x^{n+m}=x^nx^m\) for all \(n\geqslant 1\text{.}\) The basis for this proof follows directly from the basis for the definition of exponentiation.
Induction: Assume that for some \(m\geq 1\text{,}\) \(p(m)\) is true. Then
\begin{equation*}
\begin{split}
x^{n+(m+1)} & =x^{(n+m)+1}\quad \textrm{by associativity of integer addition}\\
&=x^{n+m}x^1 \quad \textrm{ by recursive definition}\\
&=x^nx^mx^1 \quad \textrm{induction hypothesis}\\
&=x^nx^{m+1}\quad \textrm{recursive definition}\quad \square\\
\end{split}
\end{equation*}
3.8 Quantifiers
3.8.5 Exercises
3.8.5.1.
3.8.5.3.
Answer.
-
There is a book with a cover that is not blue.
-
Every mathematics book that is published in the United States has a blue cover.
-
There exists a mathematics book with a cover that is not blue.
-
There exists a book that appears in the bibliography of every mathematics book.
-
\(\displaystyle (\forall x)(B(x)\to M(x))\)
-
\(\displaystyle (\exists x)(M(x)\land \neg U(x))\)
-
\(\displaystyle (\exists x)((\forall y)(\neg R(x,y))\)
3.8.5.5.
3.8.5.7.
3.8.5.9.
3.8.5.10.
3.8.5.11.
3.9 A Review of Methods of Proof
3.9.3 Exercises
3.9.3.1.
Answer.
The given statement can be written in if \(\dots\) , then \(\dots\) format as: If \(x\) and \(y\) are two odd positive integers, then \(x+y\) is an even integer.
Proof: Assume \(x\) and \(y\) are two positive odd integers. It can be shown that \(x+y=2 \cdot \textrm{(some positive integer)}\text{.}\)
Then,
\begin{equation*}
x+y=(2m+1)+(2n+1)=2((m+n)+1)=2\cdot\textrm{(some positive integer)}
\end{equation*}
Therefore, \(x+y\) is an even positive integer. \(\square\)
3.9.3.3.
Answer.
Proof: (Indirect) Assume to the contrary, that \(\sqrt{2}\) is a rational number. Then there exists \(p,q\in \mathbb{Z}, (q\neq 0)\) where \(\frac{p}{q}=\sqrt{2}\) and where \(\frac{p}{q}\) is in lowest terms, that is, \(p\) and \(q\) have no common factor other than 1.
\begin{equation*}
\begin{split}
\frac{p}{q}=\sqrt{2} & \Rightarrow \frac{p^2}{q^2}=2\\
&\Rightarrow p^2=2 q^2 \\
&\Rightarrow p^2 \textrm{ is an even integer}\\
&\Rightarrow p \textrm{ is an even integer (see Exercise 2)}\\
&\Rightarrow \textrm{4 is a factor of }p^2\\
&\Rightarrow q^2 \textrm{ is even}\\
&\Rightarrow q \textrm{ is even}\\
\end{split}
\end{equation*}
3.9.3.5.
Answer.
Proof: (Indirect) Assume \(x,y\in \mathbb{R}\) and \(x+y\leqslant 1\text{.}\) Assume to the contrary that \(\left(x\leqslant \frac{1}{2}\textrm{ or } y\leqslant \frac{1}{2}\right)\) is false, which is equivalent to \(x>\frac{1}{2}\textrm{ and } y>\frac{1}{2}\text{.}\) Hence \(x+y>\frac{1}{2}+\frac{1}{2}=1\text{.}\) This contradicts the assumption that \(x+y\leqslant 1\text{.}\) \(\square\)
4 More on Sets
4.1 Methods of Proof for Sets
4.1.5 Exercises
4.1.5.1.
Answer.
-
Assume that \(x\in A\) (condition of the conditional conclusion \(A \subseteq C\)). Since \(A \subseteq B\text{,}\) \(x\in B\) by the definition of \(\subseteq\text{.}\) \(B\subseteq C\) and \(x\in B\) implies that \(x\in C\text{.}\) Therefore, if \(x\in A\text{,}\) then \(x\in C\text{.}\) \(\square\)
-
(Proof that \(A -B \subseteq A\cap B^c\)) Let \(x\) be in \(A - B\text{.}\) Therefore, x is in \(A\text{,}\) but it is not in B; that is,\(\text{ }x \in A\) and \(x \in B^c \Rightarrow x\in A\cap B^c\text{.}\) \(\square\)
-
\((\Rightarrow )\)Assume that \(A \subseteq B\) and \(A \subseteq C\text{.}\) Let \(x\in A\text{.}\) By the two premises,\(x\in B\) and \(x\in C\text{.}\) Therefore, by the definition of intersection, \(x\in B\cap C\text{.}\) \(\square\)
-
\((\Rightarrow )\)(Indirect) Assume that \(B^c\) is not a subset of \(A^c\) . Therefore, there exists \(x\in B^c\) that does not belong to \(A^c\text{.}\) \(x \notin A^c \Rightarrow x \in A\text{.}\) Therefore, \(x\in A\) and \(x\notin B\text{,}\) a contradiction to the assumption that \(A\subseteq B\text{.}\) \(\square\)
-
There are two cases to consider. The first is when \(C\) is empty. Then the conclusion follows since both Cartesian products are empty.If \(C\) isn’t empty, we have two subcases, if \(A\) is empty, \(A\times C = \emptyset\text{,}\) which is a subset of every set. Finally, the interesting subcase is when \(A\) is not empty. Now we pick any pair \((a,c) \in A\times C\text{.}\) This means that \(a\) is in \(A\) and \(c\) is in \(C\text{.}\) Since \(A\) is a subset of \(B\text{,}\) \(a\) is in \(B\) and so \((a,c) \in B \times C\text{.}\) Therefore \(A\times C \subseteq B\times C\text{.}\) \(\square\)
4.1.5.3.
Answer.
-
If \(A = \mathbb{Z}\) and \(B=\emptyset\text{,}\) \(A - B = \pmb{\mathbb{Z}}\text{,}\) while \(B - A = \emptyset\text{.}\)
-
If \(A=\{0\}\) and \(B = \{1\}\text{,}\) \((0,1) \in A \times B\text{,}\) but \((0, 1)\) is not in \(B\times A\text{.}\)
-
If \(A = \{1\}\text{,}\) \(B = \{1\}\text{,}\) and \(C =\emptyset\text{,}\) then the left hand side of the identity is \(\{1\}\) while the right hand side is the empty set. Another example is \(A = \{1,2\}\text{,}\) \(B = \{1\}\text{,}\) and \(C =\{2\}.\)
4.1.5.5.
Solution.
Proof: Let \(p(n)\) be
\begin{equation*}
A\cap (B_1\cup B_2\cup \cdots \cup B_n)=(A\cap B_1)\cup (A\cap B_2)\cup \cdots \cup (A\cap B_n)\text{.}
\end{equation*}
Basis: We must show that \(p(2) : A \cap (B_1 \cup B_2 )=(A\cap B_1) \cup (A\cap B_2)\) is true. This was done by several methods in section 4.1.
Induction: Assume for some \(n\geq 2\) that \(p(n)\) is true. Then
\begin{equation*}
\begin{split}
A\cap (B_1\cup B_2\cup \cdots \cup B_{n+1})&=A\cap ((B_1\cup B_2\cup \cdots \cup B_n)\cup B_{n+1})\\
&=(A \cap (B_1\cup B_2\cup \cdots \cup B_n))\cup (A\cap B_{n+1}) \quad \textrm{by } p(2)\\
&=((A\cap B_1)\cup \cdots \cup (A\cap B_n))\cup (A\cap B_{n+1})\quad \textrm{by the induction hypothesis}\\
&=(A\cap B_1)\cup \cdots \cup (A\cap B_n)\cup (A\cap B_{n+1})\quad \square\\
\end{split}
\end{equation*}
4.1.5.6.
Answer.
The statement is false. The sets \(A=\{1,2\}\text{,}\) \(B=\{2,3\}\) and \(C=\{3,4\}\) provide a counterexample. Looking ahead to Chapter 6, we would say that the relation of being non-disjoint is not transitive 6.3.3
4.2 Laws of Set Theory
4.2.4 Exercises
4.2.4.1.
Answer.
-
\begin{equation*} \begin{array}{ccccccc} A & B &A^c & B^c & A\cup B & (A\cup B)^c &A^c\cap B^c \\ \hline 0 & 0 &1 & 1 & 0 & 1 & 1 \\ 0 & 1 &1 & 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 1 & 1 & 0 & 0 \\ 1 & 1 & 0 & 0 & 1 & 0 & 0 \\ \end{array} \end{equation*}The last two columns are the same so the two sets must be equal.
-
\begin{equation*} \begin{split} x\in A\cup A & \Rightarrow (x\in A) \lor (x\in A)\quad\textrm{by the definition of } \cap\\ &\Rightarrow x\in A \quad\textrm{ by the idempotent law of logic} \end{split} \end{equation*}Therefore, \(A\cup A\subseteq A\text{.}\)\begin{equation*} \begin{split} x\in A &\Rightarrow (x\in A) \lor (x\in A) \quad \textrm{ by conjunctive addition}\\ & \Rightarrow x\in A\cup A\\ \end{split} \end{equation*}Therefore, \(A \subseteq A\cup A\) and so we have \(A\cup A=A\text{.}\)
4.2.4.3.
Answer.
For all parts of this exercise, a reason should be supplied for each step. We have supplied reasons only for part a and left them out of the other parts to give you further practice.
-
\begin{equation*} \begin{split} A \cup (B-A)&=A\cup (B \cap A^c) \textrm{ by Exercise 1 of Section 4.1}\\ & =(A\cup B)\cap (A\cup A^c) \textrm{ by the distributive law}\\ &=(A\cup B)\cap U \textrm{ by the null law}\\ &=(A\cup B) \textrm{ by the identity law } \square \end{split}\text{.} \end{equation*}
-
\begin{equation*} \begin{split} A - B & = A \cap B ^c\\ & =B^c\cap A\\ &=B^c\cap (A^c)^c\\ &=B^c-A^c\\ \end{split}\text{.} \end{equation*}
-
Select any element, \(x \in A\cap C\text{.}\) One such element exists since \(A\cap C\) is not empty.\begin{equation*} \begin{split} x\in A\cap C\ &\Rightarrow x\in A \land x\in C \\ & \Rightarrow x\in B \land x\in C \\ & \Rightarrow x\in B\cap C \\ & \Rightarrow B\cap C \neq \emptyset \quad \square \\ \end{split}\text{.} \end{equation*}Therefore,
-
\begin{equation*} \begin{split} A\cap (B-C) &=A\cap (B\cap C^c) \\ & = (A\cap B\cap A^c)\cup (A\cap B\cap C^c) \\ & =(A\cap B)\cap (A^c\cup C^c) \\ & =(A\cap B)\cap (A\cup C)^c \\ & =(A-B)\cap (A-C) \quad \square\\ \end{split}\text{.} \end{equation*}
-
\begin{equation*} \begin{split} A-(B\cup C)& = A\cap (B\cup C)^c\\ & =A\cap (B^c\cap C^c)\\ & =(A\cap B^c)\cap (A\cap C^c)\\ & =(A-B)\cap (A-C) \quad \square\\ \end{split}\text{.} \end{equation*}
4.2.4.5. Hierarchy of Set Operations.
4.3 Minsets
4.3.3 Exercises
4.3.3.1.
4.3.3.3.
4.3.3.5.
4.3.3.7.
Answer.
Let \(a\in A\text{.}\) For each \(i\text{,}\) \(a\in B_i\text{,}\) or \(a\in B_i{}^c\text{,}\) since \(B_i\cup B_i{}^c=A\) by the complement law. Let \(D_i=B_i\) if \(a\in B_i\text{,}\) and \(D_i=B_i{}^c\) otherwise. Since \(a\) is in each \(D_i\text{,}\) it must be in the minset \(D_1\cap D_2 \cdots \cap D_n\text{.}\) Now consider two different minsets \(M_1= D_1\cap D_2\cdots \cap D_n\text{,}\) and \(M_2=G_1\cap G_2\cdots \cap G_n\text{,}\) where each \(D_i\) and \(G_i\) is either \(B_i\) or \(B_i{}^c\text{.}\) Since these minsets are not equal, \(D_i\neq G_i\text{,}\) for some \(i\text{.}\) Therefore, \(M_1\cap M_2=D_1\cap D_2 \cdots \cap D_n\cap G_1\cap G_2\cdots \cap G_n=\emptyset\text{,}\) since two of the sets in the intersection are disjoint. Since every element of \(A\) is in a minset and the minsets are disjoint, the nonempty minsets must form a partition of \(A\text{.}\) \(\square\)
4.4 The Duality Principle
4.4.2 Exercises
4.4.2.1.
4.4.2.3.
4.4.2.5.
Answer.
The maxsets are:
-
\(\displaystyle B_1\cup B_2=\{1,2,3,5\}\)
-
\(\displaystyle B_1\cup B_2{}^c=\{1,3,4,5,6\}\)
-
\(\displaystyle B_1{}^c\cup B_2=\{1,2,3,4,6\}\)
-
\(\displaystyle B_1{}^c\cup B_2{}^c=\{2,4,5,6\}\)
They do not form a partition of \(A\) since it is not true that the intersection of any two of them is empty. A set is said to be in maxset normal form when it is expressed as the intersection of distinct nonempty maxsets or it is the universal set \(U\text{.}\)
5 Introduction to Matrix Algebra
5.1 Basic Definitions and Operations
5.1.4 Exercises
5.1.4.1.
Answer.
For parts c, d and i of this exercise, only a verification is needed. Here, we supply the result that will appear on both sides of the equality.
-
\(\displaystyle AB=\left( \begin{array}{cc} -3 &6 \\ 9 & -13 \\ \end{array} \right) \quad BA=\left( \begin{array}{cc} 2 & 3 \\ -7 & -18 \\ \end{array} \right)\)
-
\(\displaystyle \left( \begin{array}{cc} 1 & 0 \\ 5 & -2 \\ \end{array} \right)\)
-
\(\displaystyle \left( \begin{array}{cc} 3 & 0 \\ 15 & -6 \\ \end{array} \right)\)
-
\(\displaystyle \left( \begin{array}{ccc} 18 & -15 & 15 \\ -39 & 35 & -35 \\ \end{array} \right)\)
-
\(\displaystyle \left( \begin{array}{ccc} -12 & 7 & -7 \\ 21 & -6 & 6 \\ \end{array} \right)\)
-
\(\displaystyle B+0=B\)
-
\(\displaystyle \left( \begin{array}{cc} 0 & 0 \\ 0 & 0 \\ \end{array} \right)\)
-
\(\displaystyle \left( \begin{array}{cc} 0 & 0 \\ 0 & 0 \\ \end{array} \right)\)
-
\(\displaystyle \left( \begin{array}{cc} 5 & -5 \\ 10 & 15 \\ \end{array} \right)\)
5.1.4.3.
5.1.4.5.
5.1.4.7.
Answer.
-
\(Ax=\left( \begin{array}{c} 2x_1+1x_2 \\ 1x_1-1x_2 \\ \end{array} \right)\) equals \(\left( \begin{array}{c} 3 \\ 1 \\ \end{array} \right)\) if and only if both of the equalities \(2x_1+x_2=3 \textrm{ and } x_1-x_2=1\) are true.
-
(i) \(A=\left( \begin{array}{cc} 2 & -1 \\ 1 & 1 \\ \end{array} \right)\) \(x=\left( \begin{array}{c} x_1 \\ x_2 \\ \end{array} \right)\) \(B=\left( \begin{array}{c} 4 \\ 0 \\ \end{array} \right)\)
-
\(A=\left( \begin{array}{ccc} 1 & 1 & 2 \\ 1 & 2 & -1 \\ 1 & 3 & 1 \\ \end{array} \right)\) \(x=\left( \begin{array}{c} x_1 \\ x_2 \\ x_3 \\ \end{array} \right)\) \(B=\left( \begin{array}{c} 1 \\ -1 \\ 5 \\ \end{array} \right)\)
-
\(A=\left( \begin{array}{ccc} 1 & 1 & 0 \\ 0 & 1 & 0 \\ 1 & 0 & 3 \\ \end{array} \right)\) \(x=\left( \begin{array}{c} x_1 \\ x_2 \\ x_3 \\ \end{array} \right)\) \(B=\left( \begin{array}{c} 3 \\ 5 \\ 6 \\ \end{array} \right)\)
5.2 Special Types of Matrices
5.2.3 Exercises
5.2.3.1.
Answer.
-
\(\displaystyle \left( \begin{array}{cc} -1/5 & 3/5 \\ 2/5 & -1/5 \\ \end{array} \right)\)
-
No inverse exists.
-
\(\displaystyle \left( \begin{array}{cc} 1 & 3 \\ 0 & 1 \\ \end{array} \right)\)
-
\(\displaystyle A^{-1}=A\)
-
\(\displaystyle \left( \begin{array}{ccc} 1/3 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & -1/5 \\ \end{array} \right)\)
5.2.3.3.
Solution.
The object here is to prove a formula for the inverse of \(AB\text{,}\) which is denoted \((AB)^(-1)\text{.}\) If \(A^(-1) B^(-1)\) inverts \(AB\) (which it does) then the formula is proven.
\begin{equation*}
\begin{split}
\left(B^{-1}A^{-1}\right)(AB)&=\left(B^{-1}\right)\left(A^{-1}(AB)\right)\\
&= \left(B^{-1}\right) \left(\left(A^{-1} A\right) B\right)\\
&=(\left(B^{-1}\right)I B )\\
&=B^{-1}(B)\\
&=I
\end{split}
\end{equation*}
Similarly, \((AB)\left(B^{-1}A^{-1}\right)=I\text{.}\)
By Theorem 5.2.6, \(B^{-1}A^{-1}\) is the only inverse of \(AB\text{.}\) If we tried to invert \(AB\) with \(A^{-1}B^{-1}\text{,}\) we would be unsuccessful since we cannot rearrange the order of the matrices.
5.2.3.5. Linearity of Determinants.
Solution.
-
Let \(A=\left( \begin{array}{cc} a & b \\ c & d \\ \end{array} \right)\) and \(B=\left( \begin{array}{cc} x & y \\ z & w \\ \end{array} \right)\text{.}\)\begin{equation*} \begin{split} \det(A B) & =\det \left( \begin{array}{cc} a x+b z & a y+b w \\ c x+d z & c y+d w \\ \end{array} \right)\\ &=a d w x-a d y z-b c w x+b c y z \quad \text{four terms cancel}\\ &=(ad-bc)x w - (ad -bc)y z\\ &=(ad-bc)(x w - y z)\\ &=(\det A)(\det B) \end{split}\text{.} \end{equation*}
-
\(1=\det I=\det \left(AA^{-1}\right)=\det A\text{ }\det A^{-1}\text{.}\) Now solve for \(\det A^{-1}\text{.}\)
-
\(\det A=1\cdot 1 - 3 \cdot 2 =-5\) while \(\det A^{-1}= \frac{1}{5} \cdot \frac{1}{5} - \frac{3}{5} \cdot \frac{2}{5} = -\frac{1}{5}\text{.}\)
5.2.3.7.
Answer.
Basis: \((n=1): \det A^1=\det A =(\det A )^1\)
\begin{equation*}
\begin{split}
\det A^{n+1} & =\det \left(A^nA\right)\quad \textrm{ by the definition of exponents}\\
&=\det \left(A^n\right)\det (A)\quad \textrm{ by exercise 5} \\
&=(det A)^n(\det A)\quad \textrm{ by the induction hypothesis }\\
&=(\det A)^{n+1}
\end{split}
\end{equation*}
5.2.3.9.
Answer.
-
Assume \(A=B D B^{-1}\)\begin{equation*} \begin{split} A^{m+1} &=A^mA\\ &=(B D^m B^{-1})(BDB^{-1})\quad \textrm{ by the induction hypothesis} \\ &=(BD^m(B^{-1} B ) (DB^{-1}) \quad \textrm{ by associativity} \\ &=B D^m D B^{-1} \quad \textrm{ by the definition of inverse}\\ &=B D^{m+1} B^{-1} \quad \square \end{split} \end{equation*}
-
\(\displaystyle A^{10}=BD^{10}B^{-1}= \left( \begin{array}{cc} -9206 & 15345 \\ -6138 & 10231 \\ \end{array} \right)\)
5.3 Laws of Matrix Algebra
5.3.3 Exercises
5.3.3.1.
Answer.
-
Let \(A\text{,}\) \(B\text{,}\) and \(C\) be \(m\) by \(n\) matrices. Then \(A+(B+C)=(A+B)+C\text{.}\)
-
Let \(A\) and \(B\) be \(m\) by \(n\) matrices, and let \(c\in \mathbb{R}\text{.}\) Then \(c(A+B)=cA+cB\text{,}\)
-
Let \(A\) be an \(m\) by \(n\) matrix, and let \(c_1,c_2\in \mathbb{R}\text{.}\) Then \(\left(c_1+c_2\right)A=c_1A+c_2A\text{.}\)
-
Let \(A\) be an \(m\) by \(n\) matrix, and let \(c_1,c_2\in \mathbb{R}\text{.}\) Then \(c_1\left(c_2A\right)=\left(c_1c_2\right)A\)
-
Let \(\pmb{0}\) be the zero matrix, of size \(m \textrm{ by } n\text{,}\) and let \(A\) be a matrix of size \(n \textrm{ by } r\text{.}\) Then \(\pmb{0}A=\pmb{0}=\textrm{ the } m \textrm{ by } r \textrm{ zero matrix}\text{.}\)
-
Let \(A\) be an \(m \textrm{ by } n\) matrix, and \(0 = \textrm{ the number zero}\text{.}\) Then \(0A=0=\textrm{ the } m \textrm{ by } n \textrm{ zero matrix}\text{.}\)
-
Let \(A\) be an \(m \textrm{ by } n\) matrix, and let \(\pmb{0}\) be the \(m \textrm{ by } n\) zero matrix. Then \(A+\pmb{0}=A\text{.}\)
-
Let \(A\) be an \(m \textrm{ by } n\) matrix. Then \(A+(- 1)A=\pmb{0}\text{,}\) where \(\pmb{0}\) is the \(m \textrm{ by } n\) zero matrix.
-
Let \(A\text{,}\) \(B\text{,}\) and \(C\) be \(m \textrm{ by } n\text{,}\) \(n \textrm{ by } r\text{,}\) and \(n \textrm{ by } r\) matrices respectively. Then \(A(B+C)=AB+AC\text{.}\)
-
Let \(A\text{,}\) \(B\text{,}\) and \(C\) be \(m \textrm{ by } n\text{,}\) \(r \textrm{ by } m\text{,}\) and \(r \textrm{ by } m\) matrices respectively. Then \((B+C)A=BA+CA\text{.}\)
-
Let \(A\text{,}\) \(B\text{,}\) and \(C\) be \(m \textrm{ by } n\text{,}\) \(n \textrm{ by } r\text{,}\) and \(r \textrm{ by } p\) matrices respectively. Then \(A(BC)=(AB)C\text{.}\)
-
Let \(A\) be an \(m \textrm{ by } n\) matrix, \(I_m\) the \(m \textrm{ by } m\) identity matrix, and \(I_n\) the \(n \textrm{ by } n\) identity matrix. Then \(I_mA=AI_n=A\)
-
Let \(A\) be an \(n \textrm{ by } n\) matrix. Then if \(A^{-1}\) exists, \(\left(A^{-1}\right)^{-1}=A\text{.}\)
-
Let \(A\) and \(B\) be \(n \textrm{ by } n\) matrices. Then if \(A^{-1}\) and \(B^{-1}\) exist, \((AB)^{-1}=B^{-1}A^{-1}\text{.}\)
5.3.3.3.
Answer.
-
\(\displaystyle AB+AC=\left( \begin{array}{ccc} 21 & 5 & 22 \\ -9 & 0 & -6 \\ \end{array} \right)\)
-
\(\displaystyle A^{-1}=\left( \begin{array}{cc} 1 & 2 \\ 0 & -1 \\ \end{array} \right)=A\)
-
\(A(B+C)=A B+ B C\text{,}\) which is given in part (a).
-
\(\left(A^2\right)^{-1}=(AA)^{-1}=(A^{-1}A)=I^{-1}=I \quad \) by part c
5.4 Matrix Oddities
5.4.2 Exercises
5.4.2.1.
Answer.
In elementary algebra (the algebra of real numbers), each of the given oddities does not exist.
-
\(AB\) may be different from \(BA\text{.}\) Not so in elementary algebra, since \(a b = b a\) by the commutative law of multiplication.
-
There exist matrices \(A\) and \(B\) such that \(AB = \pmb{0}\text{,}\) yet \(A\neq \pmb{0}\)and \(B\neq \pmb{0}\text{.}\) In elementary algebra, the only way \(ab = 0\) is if either \(a\) or \(b\) is zero. There are no exceptions.
-
There exist matrices \(A\text{,}\) \(A\neq \pmb{0}\text{,}\) yet \(A^2=\pmb{0}\text{.}\) In elementary algebra, \(a^2=0\Leftrightarrow a=0\text{.}\)
-
There exist matrices \(A^2=A\text{.}\) where \(A\neq \pmb{0}\) and \(A\neq I\text{.}\) In elementary algebra, \(a^2=a\Leftrightarrow a=0 \textrm{ or } 1\text{.}\)
-
There exist matrices \(A\) where \(A^2=I\) but \(A\neq I\) and \(A\neq -I\text{.}\) In elementary algebra, \(a^2=1\Leftrightarrow a=1\textrm{ or }-1\text{.}\)
5.4.2.3.
5.4.2.5.
Answer.
-
\(A^{-1}=\left( \begin{array}{cc} 1/3 & 1/3 \\ 1/3 & -2/3 \\ \end{array} \right)\) \(x_1=4/3\text{,}\) and \(x_2=1/3\)
-
\(A^{-1}=\left( \begin{array}{cc} 1 & -1 \\ 1 & -2 \\ \end{array} \right)\) \(x_1=4\text{,}\) and \(x_2=4\)
-
\(A^{-1}=\left( \begin{array}{cc} 1/3 & 1/3 \\ 1/3 & -2/3 \\ \end{array} \right)\) \(x_1=2/3\text{,}\) and \(x_2=-1/3\)
-
\(A^{-1}=\left( \begin{array}{cc} 1/3 & 1/3 \\ 1/3 & -2/3 \\ \end{array} \right)\) \(x_1=0\text{,}\) and \(x_2=1\)
-
The matrix of coefficients for this system has a zero determinant; therefore, it has no inverse. The system cannot be solved by this method. In fact, the system has no solution.
6 Relations
6.1 Basic Definitions
6.1.4 Exercises
6.1.4.1.
6.1.4.3.
6.1.4.5.
Answer.
-
When \(n=3\text{,}\) there are 27 pairs in the relation.
-
Imagine building a pair of disjoint subsets of \(S\text{.}\) For each element of \(S\) there are three places that it can go: into the first set of the ordered pair, into the second set, or into neither set. Therefore the number of pairs in the relation is \(3^n\text{,}\) by the product rule.
6.1.4.7.
Solution.
Assume \((x,y)\in r_1r_3\text{.}\) This implies that there exist \(z \in A\) such that \((x,z)\in r_1\) and \((z,y)\in r_3\text{.}\) We are given that \(r_1\subseteq r_2\text{,}\) which implies that \((x,z)\in r_2\text{.}\) Combining this with \((z,y)\in r_3\) implies that \((x,y)\in r_2r_3\text{,}\) which proves that \(r_1r_3\subseteq r_2r_3\text{.}\)
6.2 Graphs of Relations on a Set
6.2.2 Exercises
6.2.2.1.
6.2.2.3.
Answer.
6.3 Properties of Relations
6.3.3 Equivalence Relations
Checkpoint 6.3.16.
Solution.
\begin{equation*}
a \equiv_n b \Rightarrow n \mid (a-b) \Rightarrow a-b=n q_1, \quad q_1 \in \mathbb{Z}
\end{equation*}
\begin{equation*}
b\equiv_n c \Rightarrow n \mid (b-c) \Rightarrow b-c=n q_2, \quad q_2 \in \mathbb{Z}
\end{equation*}
Therefore
\begin{equation*}
a-c=(a-b)+(b-c)=n(q_1+q_2) \Rightarrow a \equiv_n c
\end{equation*}
6.3.4 Exercises
6.3.4.1.
Answer.
-
“Divides” is reflexive because, if \(i\) is any positive integer, \(i\cdot 1 = i\) and so \(i \mid i\)
-
“Divides” is antisymmetric. Suppose \(i\) and \(j\) are two distinct positive integers. One of them has to be less than the other, so we will assume \(i \lt j\text{.}\) If \(i \mid j\text{,}\) then for some positive integer \(k\text{,}\) where \(k \ge 1\) we have \(i \cdot k = j\text{.}\) But this means that \(j \cdot \frac{1}{k}=i\) and since \(\frac{1}{k}\) is not a positive integer, \(j \nmid i\text{.}\)
-
“Divides” is transitive. If \(h\text{,}\) \(i\) and \(j\) are positive integers such that \(h \mid i\) and \(i \mid j\text{,}\) there must be two positive integers \(k_1\) and \(k_2\) such that \(h \cdot k_1 =i\) and \(i \cdot k_2 = j\text{.}\) Combining these equalities we get \(h \cdot (k_1 \cdot k_2) = j\) and so \(h \mid j\text{.}\)
6.3.4.3.
Answer.
| Part | reflexive? | symmetric? | antisymmetric? | transitive? |
|---|---|---|---|---|
| i | yes | no | no | yes |
| ii | yes | no | yes | yes |
| iii | no | no | no | no |
| iv | no | yes | yes | yes |
| v | yes | yes | no | yes |
| vi | yes | no | yes | yes |
| vii | no | no | no | no |
-
See Table 6.3.20
-
Graphs ii and vi show partial ordering relations. Graph v is of an equivalence relation.
6.3.4.5.
Answer.
-
No, since \(\mid 1-1\mid =0\neq 2\text{,}\) for example
-
No, since \(\mid 2-4\mid =2\) and \(\mid 4-6\mid =2\text{,}\) but \(\mid 2-6\mid =4\neq 2\text{,}\) for example.
-
See Figure 6.3.21

Solution to number 5c of section 6.3
6.3.4.7.
Answer.
Let \(a\) be any element of \(A\text{.}\) \(a\in [a]\) since \(r\) is reflexive, so each element of \(A\) is in some equivalence class. Therefore, the union of all equivalence classes equals \(A\text{.}\) Next we show that any two equivalence classes are either identical or disjoint and we are done. Let \([a]\) and \([b]\) be two equivalence classes, and assume that \([a]\cap [b]\neq \emptyset\text{.}\) We want to show that \([a]=[b]\text{.}\) To show that \([a]\subseteq [b]\text{,}\) let \(x\in [a]\text{.}\) \(x\in [a] \Rightarrow a r x \text{.}\) Also, there exists an element, \(y\text{,}\) of \(A\) that is in the intersection of \([a]\) and \([b]\) by our assumption. Therefore,
\begin{equation*}
\begin{split}
a r y \land b r y &\Rightarrow a r y \land y r b \quad r\textrm{ is symmetric}\\
&\Rightarrow a r b \quad \textrm{ transitivity of }r \\
\end{split}
\end{equation*}
Next,
\begin{equation*}
\begin{split}
a r x \land a r b &\Rightarrow x r a \land a r b\\
&\Rightarrow x r b\\
&\Rightarrow b r x\\
& \Rightarrow x \in [b]\\
\end{split}
\end{equation*}
6.3.4.9.
6.3.4.11.
6.4 Matrices of Relations
6.4.3 Exercises
6.4.3.1.
Answer.
-
\(\begin{array}{cc} & \begin{array}{ccc} 4 & 5 & 6 \\ \end{array} \\ \begin{array}{c} 1 \\ 2 \\ 3 \\ 4 \\ \end{array} & \left( \begin{array}{ccc} 0 & 0 & 0 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{array} \right) \\ \end{array}\) and \(\begin{array}{cc} & \begin{array}{ccc} 6 & 7 & 8 \\ \end{array} \\ \begin{array}{c} 4 \\ 5 \\ 6 \\ \end{array} & \left( \begin{array}{ccc} 0 & 0 & 0 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \\ \end{array} \right) \\ \end{array}\)
-
\(\displaystyle r_1r_2 =\{(3,6),(4,7)\}\)
-
\(\displaystyle \begin{array}{cc} & \begin{array}{ccc} 6 & 7 & 8 \\ \end{array} \\ \begin{array}{c} 1 \\ 2 \\ 3 \\ 4 \\ \end{array} & \left( \begin{array}{ccc} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \\ \end{array} \right) \\ \end{array}\)
6.4.3.3.
6.4.3.5.
Answer.
The graph of a relation on three elements has nine entries. The three entries in the diagonal must be 1 in order for the relation to be reflexive. In addition, to make the relation symmetric, the off-diaginal entries can be paired up so that they are equal. For example if the entry in row 1 column 2 is equal to 1, the entry in row 2 column 1 must also be 1. This means that three entries, the ones above the diagonal determine the whole matrix, so there are \(2^3=8\) different reflexive, symmetric relations on a three element set.
6.4.3.7.
Answer.
-
\(\begin{array}{cc} & \begin{array}{cccc} 1 & 2 & 3 & 4 \\ \end{array} \\ \begin{array}{c} 1 \\ 2 \\ 3 \\ 4 \\ \end{array} & \left( \begin{array}{cccc} 0 & 1 & 0 & 0 \\ 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 \\ 0 & 0 & 1 & 0 \\ \end{array} \right) \\ \end{array}\) and \(\begin{array}{cc} & \begin{array}{cccc} 1 & 2 & 3 & 4 \\ \end{array} \\ \begin{array}{c} 1 \\ 2 \\ 3 \\ 4 \\ \end{array} & \left( \begin{array}{cccc} 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 \\ 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 \\ \end{array} \right) \\ \end{array}\)
-
\(P Q= \begin{array}{cc} & \begin{array}{cccc} 1 & 2 & 3 & 4 \\ \end{array} \\ \begin{array}{c} 1 \\ 2 \\ 3 \\ 4 \\ \end{array} & \left( \begin{array}{cccc} 0 & 1 & 0 & 1 \\ 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 \\ 1 & 0 & 1 & 0 \\ \end{array} \right) \\ \end{array}\) \(P^2 =\text{ } \begin{array}{cc} & \begin{array}{cccc} 1 & 2 & 3 & 4 \\ \end{array} \\ \begin{array}{c} 1 \\ 2 \\ 3 \\ 4 \\ \end{array} & \left( \begin{array}{cccc} 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 \\ 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 \\ \end{array} \right) \\ \end{array}\)\(=Q^2\)
6.4.3.9.
Answer.
-
Antisymmetric: Assume \(R_{ij}\leq S_{ij}\) and \(S_{ij}\leq R_{ij}\) for all \(1\leq i,j\leq n\text{.}\) Therefore, \(R_{ij} = S_{ij}\) for all \(1\leq i,j\leq n\) and so \(R=S\)Transitive: Assume \(R, S,\) and \(T\) are matrices where \(R_{ij}\leq S_{ij}\) and \(S_{ij}\leq T_{ij}\text{,}\) for all \(1\leq i,j\leq n\text{.}\) Then \(R_{ij}\leq T_{ij}\) for all \(1\leq i,j\leq n\text{,}\) and so \(R\leq T\text{.}\)
-
\begin{equation*} \begin{split} \left(R^2\right)_{ij}&=R_{i1}R_{1j}+R_{i2}R_{2j}+\cdots +R_{in}R_{nj}\\ &\leq S_{i1}S_{1j}+S_{i2}S_{2j}+\cdots +S_{in}S_{nj}\\ &=\left(S^2\right)_{ij} \Rightarrow R^2\leq S^2 \end{split}\text{.} \end{equation*}To verify that the converse is not true we need only one example. For \(n=2\text{,}\) let \(R_{12}=1\) and all other entries equal \(0\text{,}\) and let \(S\) be the zero matrix. Since \(R^2\) and \(S^2\) are both the zero matrix, \(R^2\leq S^2\text{,}\) but since \(R_{12}>S_{12}, R\leq S\) is false.
-
The matrices are defined on the same set \(A=\left\{a_1,a_2,\ldots ,a_n\right\}\text{.}\) Let \(c\left(a_i\right), i=1,2,\ldots ,n\) be the equivalence classes defined by \(R\) and let \(d\left(a_i\right)\) be those defined by \(S\text{.}\) Claim: \(c\left(a_i\right)\subseteq d\left(a_i\right)\text{.}\)\begin{equation*} \begin{split} a_j\in c\left(a_i\right)&\Rightarrow a_i r a_j\\ &\Rightarrow R_{ij}=1 \Rightarrow S_{ij}=1\\ &\Rightarrow a_i s a_j\\ & \Rightarrow a_j \in d\left(a_i\right)\\ \end{split} \end{equation*}
6.5 Closure Operations on Relations
6.5.3 Exercises
6.5.3.3.
Answer.
-
See graphs below.
6.5.3.5.
6.5.3.7.
Answer.
-
By the definition of transitive closure, \(r^+\) is the smallest relation which contains \(r\text{;}\) therefore, it is transitive. The transitive closure of \(r^+\text{,}\) \(\left(r^+\right)^+\) , is the smallest transitive relation that contains \(r^+\text{.}\) Since \(r^+\) is transitive, \(\left(r^+\right)^+=r^+\text{.}\)
-
The transitive closure of a symmetric relation is symmetric, but it may not be reflexive. If one element is not related to any elements, then the transitive closure will not relate that element to others.
7 Functions
7.1 Definition and Notation
7.1.5 Exercises
7.1.5.1.
7.1.5.3.
7.1.5.5.
7.2 Properties of Functions
7.2.3 Exercises
7.2.3.1.
7.2.3.3.
7.2.3.5.
7.2.3.7.
7.2.3.9.
Answer.
-
Use the function\(f:\mathbb{N}\to \mathbb{Z}\) defined by \(f(\text{x0}=x/2\) if \(x\) is even and \(f(x)=-(x+1)/2\) if \(x\) is odd.
-
The proof is due to Georg Cantor (1845-1918), and involves listing the rationals through a definite procedure so that none are omitted and duplications are avoided. In the first row list all nonnegative rationals with denominator 1, in the second all nonnegative rationals with denominator 2, etc. In this listing, of course, there are duplications, for example, \(0/1=0/2=0\text{,}\) \(1/1=3/3=1\text{,}\) \(6/4=9/6=3/2\text{,}\) etc. To obtain a list without duplications follow the arrows in Figure 7.2.15, listing only the circled numbers.We obtain: \(0,1,1/2,2,3,1/3,1/4,2/3,3/2,4/1,\ldots\) Each nonnegative rational appears in this list exactly once. We now must insert in this list the negative rationals, and follow the same scheme to obtain:\begin{equation*} 0,1,-1,1/2,-1/2,2,-2,3,-3,1/3,-1/3, \ldots \end{equation*}which can be paired off with the elements of \(\mathbb{N}\text{.}\)

7.2.3.11.
7.2.3.13.
Answer.
The proof is indirect and follows a technique called the Cantor diagonal process. Assume to the contrary that the set is countable, then the elements can be listed: \(n_1,n_2,n_3,\ldots\) where each \(n_i\) is an infinite sequence of 0s and 1s. Consider the array:
\begin{equation*}
\begin{array}{c}
n_1=n_{11}n_{12}n_{13}\cdots\\
n_2=n_{21}n_{22}n_{23}\cdots\\
n_3=n_{31}n_{32}n_{33}\cdots\\
\quad \vdots\\
\end{array}
\end{equation*}
We assume that this array contains all infinite sequences of 0s and 1s. Consider the sequence \(s\) defined by \(s_i=\begin{cases}
0 & \textrm{ if } n_{\textrm{ii}}=1 \\
1 & \textrm{ if } n_{\textrm{ii}}=0
\end{cases}\)
Notice that \(s\) differs from each \(n_i\) in the \(i\)th position and so cannot be in the list. This is a contradiction, which completes our proof.
7.3 Function Composition
7.3.4 Exercises
7.3.4.1.
Answer.
-
\(g\circ f:A\to C\) is defined by \((g\circ f)(k)=\begin{cases} + & \textrm{ if } k=1 \textrm{ or } k=5 \\ - & \textrm{ otherwise} \end{cases}\)
-
No, since \(f\) is not surjective.
-
No, since \(g\) is not injective.
7.3.4.3.
Answer.
-
\begin{equation*} \begin{array}{ccc} g & g^{-1} & g^2 \\ i & i & i \\ r_1 & r_2 & r_2 \\ r_2 & r_1 & r_1 \\ f_1 & f_1 & i \\ f_2 & f_2 & i \\ f_3 & f_3 & i \\ \end{array} \end{equation*}
-
If \(f\) and \(g\) are permutations of \(A\text{,}\) then they are both injections and their composition, \(f\circ g\text{,}\) is a injection, by Theorem 7.3.6. By Theorem 7.3.7, \(f\circ g\) is also a surjection; therefore, \(f\circ g\) is a bijection on \(A\text{,}\) a permutation.
-
Proof by induction: Basis: \((n=1)\text{.}\) The number of permutations of \(A\) is one, the identity function, and 1! \(=1\text{.}\)Induction: Assume that the number of permutations on a set with \(n\) elements, \(n\geq 1\text{,}\) is \(n\text{!.}\) Furthermore, assume that \(|A|=\)\(\text{ }n+1\) and that \(A\) contains an element called \(\sigma\text{.}\) Let \(A'=A-\{\sigma\}\text{.}\) We can reduce the definition of a permutation, \(f\text{,}\) on \(A\) to two steps. First, we select any one of the \(n\text{!}\) permutations on \(A'\text{.}\) (Note the use of the induction hypothesis.) Call it \(g\text{.}\) This permutation almost completely defines a permutation on \(A\) that we will call \(f\text{.}\) For all \(a\) in \(A'\text{,}\) we start by defining \(f(a)\) to be \(g(a)\text{.}\) We may be making some adjustments, but define it that way for now. Next, we select the image of \(\sigma\text{,}\) which can be done \(n+1\) different ways, allowing for any value in \(A\text{.}\) To keep our function bijective, we must adjust \(f\) as follows: If we select \(f(\sigma)=y \neq \sigma\text{,}\) then we must find the element, \(z\text{,}\) of \(A\) such that \(g(z)=y\text{,}\) and redefine the image of \(z\) to \(f(z)=\sigma\text{.}\) If we had selected \(f(\sigma)=\sigma\text{,}\) then there is no adjustment needed. By the rule of products, the number of ways that we can define \(f\) is \(n!(n+1)=(n+1)!\) \(\square\)
7.3.4.5.
Answer.
-
\(f_3\) does not have an inverse. One way to verify this is to note that \(f_3\) is not one-to-one because \(f_3(0000) = 0000 = f_3(1111)\text{.}\)
7.3.4.7.
7.3.4.9.
7.3.4.11.
Answer.
Proof: Suppose that \(g\) and \(h\) are both inverses of \(f\text{,}\) both having domain \(B\) and codomain \(A\text{.}\)
\begin{equation*}
\begin{split}g &= g\circ i_B \\
& =g\circ (f\circ h)\\
& =(g\circ f)\circ h\\
& =i_A\circ h\\
& =h\quad \Rightarrow g=h \quad \square
\end{split}
\end{equation*}
7.3.4.12.
7.3.4.13.
Answer.
Let \(x,x'\) be elements of \(A\) such that \(g\circ f(x)=g\circ f(x')\text{;}\) that is, \(g(f(x))=g(f(x'))\text{.}\) Since \(g\) is injective, \(f(x)=f(x')\) and since \(f\) is injective, \(x=x'\text{.}\) \(\square\)
Let \(x\) be an element of \(C\text{.}\) We must show that there exists an element of \(A\) whose image under \(g\circ f\) is \(x\text{.}\) Since \(g\) is surjective, there exists an element of \(B\text{,}\) \(y\text{,}\) such that \(g(y)=x\text{.}\) Also, since \(f\) is a surjection, there exists an element of \(A\text{,}\) \(z\text{,}\) such that \(f(z)=y\text{,}\) \(g\circ f(z)=g(f(z))=g(y)=x\text{.}\)\(\square\)
7.3.4.15.
Answer.
Basis: \((n=2)\text{:}\) \(\left(f_1\circ f_2\right){}^{-1}=f_2{}^{-1}\circ f_1{}^{-2}\) by Exercise 7.3.4.12.
Induction: Assume \(n\geq 2\) and
\begin{equation*}
\left(f_1\circ f_2\circ \cdots \circ f_n\right){}^{-1}= f_n{}^{-1}\circ \cdots \circ f_2{}^{-1}\circ f_1{}^{-1}
\end{equation*}
and consider \(\left(f_1\circ f_2\circ \cdots \circ f_{n+1}\right)^{-1}\text{.}\)
\begin{equation*}
\begin{split}
\left(f_1\circ f_2\circ \cdots \circ f_{n+1}\right){}^{-1} &=\left(\left(f_1\circ f_2\circ \cdots \circ f_n\right)\circ f_{n+1}\right){}^{-1}\\
& =f_{n+1}{}^{-1}\circ \left(f_1\circ f_2\circ \cdots \circ f_n\right){}^{-1}\\
& \quad \quad \quad \textrm{ by the basis}\\
&=f_{n+1}{}^{-1}\circ \left(f_n{}^{-1}\circ \cdots \circ f_2{}^{-1}\circ f_1{}^{-1}\right)\\
& \quad \quad \quad \textrm{ by the induction hypothesis}\\
&=f_{n+1}{}^{-1}\circ \cdots \circ f_2{}^{-1}\circ f_1{}^{-1} \quad. \square
\end{split}
\end{equation*}
8 Recursion and Recurrence Relations
8.1 The Many Faces of Recursion
8.1.8 Exercises
8.1.8.1.
Answer.
\begin{equation*}
\begin{split}
\binom{7}{2} &=\binom{6}{2} +\binom{6}{1} \\
&=\binom{5}{2} +\binom{5}{1} +\binom{5}{1} +\binom{5}{0} \\
&=\binom{5}{2} +2 \binom{5}{1} +1\\
&=\binom{4}{2} +\binom{4}{1} +2(\binom{4}{1} +\binom{4}{0} )+1\\
&=\binom{4}{2} +3 \binom{4}{1} + 3\\
&=\binom{3}{2} +\binom{3}{1} +3(\binom{3}{1} +\binom{3}{0} )+3\\
&=\binom{3}{2} +4 \binom{3}{1} + 6\\
&=\binom{2}{2} +\binom{2}{1} + 4(\binom{2}{1} +\binom{2}{0} ) + 6\\
&=5 \binom{2}{1} + 11\\
&=5(\binom{1}{1} +\binom{1}{0} ) + 11\\
&=21
\end{split}
\end{equation*}
8.1.8.3.
8.1.8.5.
8.2 Sequences
8.2.3 Exercises
8.2.3.1.
Answer.
8.2.3.3.
Answer.
Imagine drawing line \(k\) in one of the infinite regions that it passes through. That infinite region is divided into two infinite regions by line \(k\text{.}\) As line \(k\) is drawn through every one of the \(k-1\) previous lines, you enter another region that line \(k\) divides. Therefore \(k\) regions are divided and the number of regions is increased by \(k\text{.}\) From this observation we get \(P(5)=16\text{.}\)
8.2.3.5.
8.3 Recurrence Relations
8.3.5 Exercises
8.3.5.13.
Answer.
-
The characteristic equation is \(a^2-a-1=0\text{,}\) which has solutions \(\alpha =\left.\left(1+\sqrt{5}\right)\right/2\) and \(\beta =\left.\left(1-\sqrt{5}\right)\right/2\text{,}\) It is useful to point out that \(\alpha +\beta =1\) and \(\alpha -\beta =\sqrt{5}\text{.}\) The general solution is \(F(k)=b_1\alpha ^k+b_2\beta ^k\text{.}\) Using the initial conditions, we obtain the system: \(b_1+b_2=1\) and \(b_1\alpha +b_2\beta =1\text{.}\) The solution to this system is \(b_1=\alpha /(\alpha -\beta )=\left.\left(5+\sqrt{5}\right)\right/2\sqrt{5}\) and \(b_2=\beta /(\alpha -\beta )=\left.\left(5-\sqrt{5}\right)\right/2\sqrt{5}\)Therefore the final solution is\begin{equation*} \begin{split} F(n) & = \frac{\alpha^{n+1}-\beta^{n+1}}{\alpha-\beta} \\ & = \frac{\left(\left.\left(1+\sqrt{5}\right)\right/2\right)^{n+1} -\left(\left.\left(1-\sqrt{5}\right)\right/2\right)^{n+1}}{\sqrt{5}}\\ \end{split} \end{equation*}
-
\(\displaystyle C_r=F(r+1)\)
8.3.5.15.
Answer.
-
For each two-block partition of \(\{1,2,\dots, n-1\}\text{,}\) there are two partitions we can create when we add \(n\text{,}\) but there is one additional two-block partition to count for which one block is \(\{n\}\text{.}\) Therefore, \(D(n)=2D(n-1)+1 \textrm{ for } n \geq 2 \textrm{ and } D(1)=0.\)
-
\(\displaystyle D(n)=2^{n-1}-1\)
8.4 Some Common Recurrence Relations
8.4.5 Exercises
8.4.5.1.
8.4.5.3.
8.4.5.4.
8.4.5.5.
8.4.5.7.
Answer.
-
A good approximation to the solution of this recurrence relation is based on the following observation: \(n\) is a power of a power of two; that is, \(n\) is \(2^m\text{,}\) where \(m=2^k\) , then \(Q(n)=1+Q\left(2^{m/2}\right)\text{.}\) By applying this recurrence relation \(k\) times we obtain \(Q(n)=k\text{.}\) Going back to the original form of \(n\text{,}\) \(\log _2n=2^k\) or \(\log _2\left(\log _2n\right)=k\text{.}\) We would expect that in general, \(Q(n)\) is \(\left\lfloor \log _2\left(\log _2n\right)\right\rfloor\text{.}\) We do not see any elementary method for arriving at an exact solution.
-
Suppose that \(n\) is a positive integer with \(2^{k-1} \leq n < 2^k\text{.}\) Then \(n\) can be written in binary form, \(\left(a_{k-1}a_{k-2}\cdots a_2a_1a_0\right)_{\textrm{two}}\) with \(a_{k-1}=1\) and \(R(n)\) is equal to the sum \(\underset{i=0}{\overset{k-1}{\Sigma }}\) \(\left(a_{k-1}a_{k-2}\cdots a_i\right)_{\textrm{two}}\text{.}\) If \(2^{k-1}\leq n < 2^k\text{,}\) then we can estimate this sum to be between \(2n-1\) and \(2n+1\text{.}\) Therefore, \(R(n)\approx 2n\text{.}\)
8.5 Generating Functions
8.5.7 Exercises
8.5.7.1.
8.5.7.3.
8.5.7.5.
8.5.7.7.
8.5.7.9.
9 Graph Theory
9.1 Graphs - General Introduction
9.1.5 Exercises
9.1.5.1.
Answer.
In Figure 9.1.8, computer \(b\) can communicate with all other computers. In Figure 9.1.9, there are direct roads to and from city \(b\) to all other cities.
9.1.5.3.
9.1.5.5.
9.1.5.7.
9.1.5.9.
Answer.
-
Not graphic - if the degree of a graph with seven vertices is 6, it is connected to all other vertices and so there cannot be a vertex with degree zero.
-
Graphic. One graph with this degree sequence is a cycle of length 6.
-
Not Graphic. The number of vertices with odd degree is odd, which is impossible.
-
Graphic. A "wheel graph" with one vertex connected to all other and the others connected to one another in a cycle has this degree sequence.
-
Graphic. Pairs of vertices connected only to one another.
-
Not Graphic. With two vertices having maximal degree, 5, every vertex would need to have a degree of 2 or more, so the 1 in this sequence makes it non-graphic.
9.2 Data Structures for Graphs
9.2.3 Exercises
9.2.3.1.
Answer.
-
A rough estimate of the number of vertices in the “world airline graph” would be the number of cities with population greater than or equal to 100,000. This is estimated to be around 4,100. There are many smaller cities that have airports, but some of the metropolitan areas with clusters of large cities are served by only a few airports. 4,000-5,000 is probably a good guess. As for edges, that’s a bit more difficult to estimate. It’s certainly not a complete graph. Looking at some medium sized airports such as Manchester, NH, the average number of cities that you can go to directly is in the 50-100 range. So a very rough estimate would be \(\frac{75 \cdot 4500}{2}=168,750\text{.}\) This is far less than \(4,500^2\text{,}\) so an edge list or dictionary of some kind would be more efficient.
-
The number of ASCII characters is 128. Each character would be connected to \(\binom{8}{2}=28\) others and so there are \(\frac{128 \cdot 28}{2}=3,584\) edges. Comparing this to the \(128^2=16,384\text{,}\) an array is probably the best choice.
-
The Oxford English Dictionary as approximately a half-million words, although many are obsolete. The number of edges is probably of the same order of magnitude as the number of words, so an edge list or dictionary is probably the best choice.
9.2.3.3.
9.3 Connectivity
9.3.6 Exercises
9.3.6.1.
9.3.6.3.
9.3.6.5.
Answer.
-
The eccentricity of each vertex is 2; and the diameter and radius are both 2 as well. All vertices are part of the center.
-
The corners (1,3,10 and 10) have eccentricities 5. The two central vertices, 5 and 8, which are in the center of the graph have eccentricity 3. All other vertices have eccentricity 4. The diameter is 5. The radius is 3.
-
Vertices 1, 2 and 5 have eccentricity 2 and make up the center of this graph. Verticies 7 and 8 have eccentricity 4, and all other vertices have eccentricity 3. The diameter is 4. The radius is 2.
-
The eccentricity of each vertex is 4; and the diameter and radius are both 4 as well. All vertices are part of the center.
9.3.6.7.
Answer.
Basis: \((k=1)\) Is the relation \(r^1\text{,}\) defined by \(v r^1 w\) if there is a path of length 1 from \(v \text{ to } w\text{?}\) Yes, since \(v r w\) if and only if an edge, which is a path of length \(1\text{,}\) connects \(v\) to \(w\text{.}\)
Induction: Assume that \(v r^k w\) if and only if there is a path of length \(k\) from \(v\) to \(w\text{.}\) We must show that \(v r^{k+1} w\) if and only if there is a path of length \(k+1\) from \(v\) to \(w\text{.}\)
\begin{equation*}
v r^{k+1} w \Rightarrow v r^k y \textrm{ and } y r w\textrm{ for some vertex } y
\end{equation*}
By the induction hypothesis, there is a path of length \(k\) from \(v \textrm{ to } y\text{.}\) And by the basis, there is a path of length one from \(y\) to \(w\text{.}\) If we combine these two paths, we obtain a path of length \(k+1\) from \(v\) to \(w\text{.}\) Of course, if we start with a path of length \(k+1\) from \(v\) to \(w\text{,}\) we have a path of length \(k\) from \(v\) to some vertex \(y\) and a path of length 1 from \(y\) to \(w\text{.}\) Therefore, \(v r^k y \textrm{ and } y r w \Rightarrow v r^{k+1} w\text{.}\)
9.3.6.9.
Answer.
Let \(v\) and \(w\) be any two vertices in the graph and let \(z\) be any vertex in the center of the graph. The distances from \(z\) to both \(v\) and \(w\) must bot be less than or equal to \(r\text{,}\) therefore, a path from \(v\) to \(w\) through \(z\) must exist and have length less than or equal to \(2r\text{.}\) Therefore \(2r\) serves as an upper bound of the diameter.
9.4 Traversals: Eulerian and Hamiltonian Graphs
9.4.3 Exercises
9.4.3.1.
Answer.
Using a recent road map, it appears that an Eulerian circuit exists in New York City, not including the small islands that belong to the city. Lowell, Massachusetts, is located at the confluence of the Merrimack and Concord rivers and has several canals flowing through it. No Eulerian path exists for Lowell.
9.4.3.3.
9.4.3.5.
9.4.3.7.
Answer.
Let \(G=(V,E)\) be a directed graph. \(G\) has an Eulerian circuit if and only if \(G\) is connected and \(indeg(v)= outdeg(v)\) for all \(v \in V\text{.}\) There exists an Eulerian path from \(v_1 \textrm{ to } v_2\) if and only if \(G\) is connected, \(indeg(v_1)=outdeg(v_1)-1\text{,}\) \(indeg(v_2)= outdeg(v_2)+1\text{,}\) and for all other vertices in \(V\) the indegree and outdegree are equal.
9.4.3.8.
9.4.3.9.
9.4.3.11.
Solution.
No, such a line does not exist. The dominoes with two different numbers correspond with edges in a \(K_6\text{.}\) See corresponding dominos and edges in Figure 9.4.25. Dominos with two equal numbers could be held back and inserted into the line created with the other dominoes if such a line exists. For example, if \((2,5),(5,4)\) were part of the line, \((5,5)\) could be inserted between those two dominoes. The line we want exists if and only if there exists an Eulerian path in a \(K_6\text{.}\) Since all six vertices of a \(K_6\) have odd degree no such path exists.
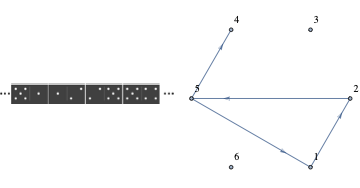
Four dominos lay end-to-end with numbers on abutting ends matching. They correspond with four connecting edges in a \(K_6\text{.}\)
9.5 Graph Optimization
9.5.5 Exercises
9.5.5.1.
9.5.5.3.
Answer.
-
Optimal cost \(=2\sqrt{2}\approx 2.82843\text{,}\) which is attained with the nearest neighbor algorithm. Strip algorithm phase 1 cost \(=3.39411\text{.}\) Strip algorithm phase 2 cost \(=3.67696\text{.}\)
-
Optimal cost \(=2.62266\text{,}\) which is attained with the nearest neighbor algorithm. Strip algorithm phase 1 cost is \(=3.00007\text{.}\) Strip algorithm phase 2 cost \(3.07119\text{.}\)
-
\(A=(0.0, 0.5), B=(0.5, 0.0), C=(0.5, 1.0), D=(1.0, 0.5)\)There are 4 points; so we will divide the unit square into two strips.
-
Optimal Path: \((B,A,C,D)\quad \quad \text{Distance } =2\sqrt{2}\)
-
Phase I Path: \((B,A,C,D)\quad \quad \text{Distance }=2\sqrt{2}\)
-
Phase II Path: \((A,C,B,D) \quad \quad\textrm{Distance }=2+\sqrt{2}\)
-
-
\(A=(0,0), B=(0.2,0.6), C=(0.4,0.1), D=(0.6,0.8), E=(0.7,0.5)\)There are 5 points; so we will divide the unit square into three strips.
-
Optimal Path: \((A,B,D,E,C)\quad \quad \text{Distance }=2.30821\)
-
Phase I Path: \((A,C,B,C,E)\quad \quad \text{Distance }=2.5745\)
-
Phase II Path: \((A,B,D,E,C) \quad \quad\textrm{Distance }=2.30821\)
-
9.5.5.5.
Answer.
-
\(f(c,d)=2\text{,}\) \(f(b,d)=2\text{,}\) \(f(d,k)=5\text{,}\) \(f(a,g)=1\text{,}\) and \(f(g,k)=1\text{.}\)
-
There are three possible flow-augmenting paths. \(s,b,d,k\) with flow increase of 1. \(s,a,d,k\) with flow increase of 1, and \(s,a,g,k\) with flow increase of 2.
-
The new flow is never maximal, since another flow-augmenting path will always exist. For example, if \(s,b,d,k\) is used above, the new flow can be augmented by 2 units with \(s,a,g,k\text{.}\)
9.5.5.7.
Answer.
-
Value of maximal flow \(=31\text{.}\)
-
Value of maximal flow \(=14\text{.}\)
| Step | Flow-augmenting path | Flow added |
| 1 | \(\text{Source},A,\text{Sink}\) | 2 |
| 2 | \(\text{Source}, C,B, \text{Sink}\) | 3 |
| 3 | \(\text{Source},E,D, \text{Sink}\) | 4 |
| 4 | \(\text{Source},A,B,\text{Sink}\) | 1 |
| 5 | \(\text{Source},C,D, \text{Sink}\) | 2 |
| 6 | \(\text{Source},A,B,C,D, \text{Sink}\) | 2 |
9.5.5.9.
Answer.
To locate the closest neighbor among the list of \(k\) other points on the unit square requires a time proportional to \(k\text{.}\) Therefore the time required for the closest-neighbor algorithm with \(n\) points is proportional to \((n-1)+(n-2)+\cdots +2+1\text{,}\) which is proportional to \(n^2\text{.}\) Since the strip algorithm takes a time proportional to \(n(\log n)\text{,}\) it is much faster for large values of \(n\text{.}\)
9.6 Planarity and Colorings
9.6.3 Exercises
9.6.3.1.
Answer.
A \(K_5\) has 10 edges. If a \(K_5\) is planar, the number of regions into which the plane is divided must be 7, by Euler’s formala (\(5+7-10=2\)). If we re-count the edges of the graph by counting the number edges bordering the regions we get a count of at least \(7 \times 3=21\text{.}\) But we’ve counted each edge twice this way and the count must be even. This implies that the number of edges is at least 11, which a contradiction.
9.6.3.2.
Hint.
Don’t forget Theorem 9.6.21!
9.6.3.3.
9.6.3.5.
9.6.3.7.
Answer.
Suppose that \(G'\) is not connected. Then \(G'\) is made up of 2 components that are planar graphs with less than \(k\) edges, \(G_1\) and \(G_2\text{.}\) For \(i=1,2\) let \(v_i,r_i, \text{and} e_i\) be the number of vertices, regions and edges in \(G_i\text{.}\) By the induction hypothesis, \(v_i+r_i-e_i=2\) for \(i=1,2\text{.}\)
One of the regions, the infinite one, is common to both graphs. Therefore, when we add edge \(e\) back to the graph, we have \(r=r_1+r_2-1\text{,}\) \(v=v_1+v_2\text{,}\) and \(e=e_1+e_2+1\text{.}\)
\begin{equation*}
\begin{split}
v+r-e &=\left(v_1+v_2\right)+\left(r_1+r_2-1\right)-\left(e_1+e_2+1\right)\\
&=\left(v_1+r_1-e_1\right)+\left(v_2+r_2-e_2\right)-2\\
&=2 + 2 -2\\
&=2
\end{split}
\end{equation*}
9.6.3.9.
Answer.
Since \(\left| E\right| +\left| E^c \right|=\frac{n(n-1)}{2}\text{,}\) either \(E \text{ or } E^c\) has at least \(\frac{n(n-1)}{4}\) elements. Assume that it is \(E\) that is larger. Since \(\frac{n(n-1)}{4}\) is greater than \(3n-6\text{ }\text{for}\text{ }n\geqslant 11\text{,}\) \(G\) would be nonplanar. Of course, if \(E^c\) is larger, then \(G'\) would be nonplanar by the same reasoning. Can you find a graph with ten vertices such that it is planar and its complement is also planar?
9.6.3.11.
Answer.
Suppose that \((V,E)\) is bipartite (with colors red and blue), \(\left| E\right|\) is odd, and \(\left(v_1,v_2,\ldots ,v_{2n+1},v_1\right)\) is a Hamiltonian circuit. If \(v_1\) is red, then \(v_{2n+1}\) would also be red. But then \(\left\{v_{2n+1},v_1\right\}\) would not be in \(E\text{,}\) a contradiction.
9.6.3.13.
9.6.3.15.
Solution.
-
The chromatic number will always be two. One coloring of any of these graphs would be to color all vertices whose coordinate add up to an even integer one color and the other vertices whose coordinates have an odd sum some other color. This works because for any vertex, if the sum of coordinate is even, the adjacent vertices differ in exactly one coordinate by \(\pm 1\) and so they have a coordinate sum that is odd.
-
If both \(a_1\) and \(a_2\) are odd, then \(M(a_1, a_2)\) does not have a Hamiltonian circuit. To see why, we can color vertices with an even coordinate sum white and the ones with a odd sum black. If \(a_1 =2k_1+1\) and \(a_2=2 k_2 + 1\text{,}\) then there are \(N=4k_1 k_2 + 2k_1+2k_2 + 1\) vertices. There will be \(k_1 k_2 + k_1+k_2 + 1\) white vertices and one fewer black one. Any circuit that starts and ends at any vertex must have an even number of vertices if we count the beginning/ending vertex once. This implies that a Hamiltonian circuit that includes all vertices cannot exist.If either of the \(a_i\) are even, \(M(a_1, a_2)\) does have a Hamiltonian circuit. There are many different possible circuits, but one of them, assuming \(a_1\) is even, would be to start at \((1,1)\text{,}\) traverse the left border, the top border and the right border, leaving you at \((a_1,1)\text{.}\) then you can zig-zag back to \((1,1)\) visiting all of the vertices in the interior of the graph and the bottom border. This is is illustrated in the following graph of \(M(4,3)\)
 A Hamiltonian circuit of \(M(4,3)\) as described in the text.
A Hamiltonian circuit of \(M(4,3)\) as described in the text. -
As in the two diminsional case there will be a Hamiltonian circuit if at least one of the \(a_i\) are even.
10 Trees
10.1 What Is a Tree?
10.1.3 Exercises
10.1.3.1.
10.1.3.3.
10.1.3.5.
Solution.
-
Assume that \((V,E)\) is a tree with \(\left| V\right| \geq 2\text{,}\) and all but possibly one vertex in \(V\) has degree two or more.\begin{equation*} \begin{split} 2\lvert E \rvert =\sum_{v \in V}{\deg(v)} \geq 2 \lvert V \rvert -1 &\Rightarrow \lvert E\vert \geq \lvert V\rvert -\frac{1}{2}\\ &\Rightarrow \lvert E\rvert \geq \lvert V\rvert\\ & \Rightarrow (V,E) \textrm{ is not a tree.} \end{split} \end{equation*}
-
The proof of this part is similar to part (a). If we assume that there are less than three vertices of degree three, we can still infer \(2\lvert E\rvert \geq 2 \lvert V\rvert -1\) using the fact that a non-chain tree has at least one vertex of degree three or more.
10.1.3.7.
Solution.
We can prove this by induction for trees with \(n\) vertices, \(n \geq 2\text{.}\) The basis is clearly true since the only tree with two vertices is a \(K_2\text{.}\) Now assume that (✶) is true for some \(n\) greater than or equal to two and consider a tree \(T\) with \(n+1\) vertices. We proceed by removing a leaf from \(T\text{.}\) If there exists a leaf connected to a vertex of degree two, we select one such leaf. The resulting tree satisfies (✶) for the number of leaves; and adding the removed leaf neither changes the number of leaves nor the value of (✶). If all interior vertices have degree three or more remove any leaf from \(T\text{.}\) Again, the number of leaves in the resulting tree is (✶), but this time when we put the removed leaf back on the tree the number of leaves will increase by one, but the value of (✶) will increase by one to match it
10.2 Spanning Trees
10.2.4 Exercises
10.2.4.1.
10.2.4.3.
Solution.
-
There are three minimal spanning tree, with edges \(\{0,5\},\{0,3\},\{4,5\}\) and any two of the following edges \(\{0,1\},\{0,2\},\{1,2\}.\)
-
There is only one minimal spanning tree. If we start with BOS as the “right set”, the edges in the following set are ordered according to how they are added in Prim’s Algorithm: \(\{\{BOS,NY\},\{NY,PHI\},\{PHI,DC\},\{DC,ATL\},\\ \{PHI,KC\},\{KC,CHI\},\{KC,LA\},\{LA,SF\}\}.\)
-
There is only one minimal spanning tree, which has edges \(\{\{1,8\},\{2,8\},\{2,7\},\{3,7\},\{3,6\},\{4,6\},\{4,5\}\}\)
10.2.4.5.
Solution.
10.2.4.7.
Solution.
-
Edges in one solution are: \(\{8,7\},\{8,9\},\{8,13\},\{7,6\},\{9,4\},\{13,12\},\\ \{13,14\},\{6,11\},\{6,1\},\{1,2\},\{4,3\},\{4,5\},\{14,15\}, \textrm{ and } \{5,10\}\)
-
Vertices 8 and 9 are centers of the graph. Starting from vertex 8, a minimum diameter spanning tree is\(\{\{8, 3\}, \{8, 7\}, \{8, 13\}, \{8, 14\}, \{8, 9\}, \{3, 2\}, \{3, 4\}, \{7, 6\},\\ \{13, 12\}, \{13, 19\}, \{14, 15\}, \{9, 16\}, \{9, 10\}, \{6, 1\}, \{12, 18\},\\ \{16, 20\}, \{16, 17\}, \{10, 11\}, \{20, 21\}, \{11, 5\}\}.\)The diameter of the tree is 7.
10.3 Rooted Trees
10.3.4 Exercises
10.3.4.1.
10.3.4.3.
10.4 Binary Trees
10.4.6 Exercises
10.4.6.1.
10.4.6.3.
Answer.
10.4.6.5.
10.4.6.7.
Answer.
Solution 1:
Basis: A binary tree consisting of a single vertex, which is a leaf, satisfies the equation \(\text{leaves} = \textrm{internal vertices} + 1\)
Induction:Assume that for some \(k\geq 1\text{,}\) all full binary trees with \(k\) or fewer vertices have one more leaf than internal vertices. Now consider any full binary tree with \(k+1\) vertices. Let \(T_A\) and \(T_B\) be the left and right subtrees of the tree which, by the definition of a full binary tree, must both be full. If \(i_A\) and \(i_B\) are the numbers of internal vertices in \(T_A\) and \(T_B\text{,}\) and \(j_A\) and \(j_B\) are the numbers of leaves, then \(j_A=i_A+1 \) and \(j_B=i_B+1\text{.}\) Therefore, in the whole tree,
\begin{equation*}
\begin{split}
\textrm{the number of leaves} & =j_A+j_B\\
&=\left(i_A+1\right)+\left(i_B+1\right)\\
&=\left(i_A+i_B+1\right)+1\\
&=(\textrm{number of internal vertices})+1
\end{split}
\end{equation*}
Solution 2:
Imagine building a full binary tree starting with a single vertex. By continuing to add leaves in pairs so that the tree stays full, we can build any full binary tree. Our starting tree satisfies the condition that the number of leaves is one more than the number of internal vertices . By adding a pair of leaves to a full binary tree, an old leaf becomes an internal vertex, increasing the number of internal vertices by one. Although we lose a leaf, the two added leaves create a net increase of one leaf. Therefore, the desired equality is maintained.
10.4.6.8.
Solution.
-
The root of \(B\) is the root of the corresponding ordered rooted tree, which as no siblings.
-
 Two columns of five graphs
Two columns of five graphsFigure 10.4.23. -
 Two columns of five graphs
Two columns of five graphsFigure 10.4.24. -
The number of ordered rooted trees with \(n\) vertices is equal to the number of binary trees with \(n-1\) vertices, \(\frac{1}{n} \binom{2(n-1)}{n-1}\)
11 Algebraic Structures
11.1 Operations
11.1.4 Exercises
11.1.4.1.
Answer.
-
Commutative, and associative. Notice that zero is the identity for addition, but it is not a positive integer.
-
Commutative, associative, and has an identity (1)
-
Commutative, associative, has an identity (1), and is idempotent
-
Commutative, associative, and idempotent
-
None. Notice that \(2 @ (3 @ 3) = 134217728\text{,}\) while \((2 @ 3) @ 3 = 512\text{;}\) and \(a @ 1 = a\text{,}\) while \(1 @ a = 1\text{.}\)
11.1.4.3.
Answer.
\begin{equation*}
\begin{split}
a, b \in A \cap B & \Rightarrow a, b \in A \textrm{ by the definition of intersection}\\
& \Rightarrow a*b \in A\textrm{ by the closure of } A \textrm{ with respect to } *
\end{split}
\end{equation*}
Similarly, \(a, b \in A \cap B \Rightarrow a*b \in B\text{.}\) Therefore, \(a * b \in A \cap B\text{.}\) The set of positive integers is closed under addition, and so is the set of negative integers, but \(1 + -1 = 0\text{.}\) Therefore, their union, the nonzero integers, is not closed under addition.
11.1.4.5.
Answer.
-
\(*\) is commutative since \(\left| a-b\right| =\left| b-a\right|\) for all \(a, b \in \mathbb{N}\)
-
\(*\) is not associative. Take \(a = 1\text{,}\) \(b = 2\text{,}\) and \(c = 3\text{,}\) then \((a * b) * c =\left| \left| 1-2\right| -3\right| =2\) , and \(a * (b * c) = \left| 1-\left| 2-3\right| \right| = 0\text{.}\)
-
Zero is the identity for \(*\) on \(\mathbb{N}\text{,}\) since \(a*0=\left| a - 0\right| = a = \left| 0-a\right| = 0 * a.\)
11.2 Algebraic Systems
11.2.4 Exercises
11.2.4.1.
Answer.
The terms “generic” and “trade” for prescription drugs are analogous to “generic” and “concrete” algebraic systems. Generic aspirin, for example, has no name, whereas Bayer, Tylenol, Bufferin, and Anacin are all trade or specific types of aspirins. The same can be said of a generic group \([G; *]\) where \(G\) is a nonempty set and \(*\) is a binary operation on \(G\text{,}\) When examples of typical domain elements can be given along with descriptions of how operations act on them, such as \(\mathbb{Q}\)* or \(M_{2\times 2}(\mathbb{R})\text{,}\) then the system is concrete (has a specific name, as with the aspirin). Generic is a way to describe a general algebraic system, whereas a concrete system has a name or symbols making it distinguishable from other systems.
11.2.4.3.
11.2.4.5.
Answer.
-
Elements are \(I=\left( \begin{array}{cc} 1 & 0 \\ 0 & 1 \\ \end{array} \right)\text{,}\) and \(T=\left( \begin{array}{cc} 0 & 1 \\ 1 & 0 \\ \end{array} \right)\text{,}\) the group is abelian. Operation table is \(\begin{array}{c|cc} \cdot & I & T\\ \hline I & I & T\\ T & T & I\\ \end{array}\)
-
\begin{equation*} \begin{array}{c|c} & \begin{array}{cccccc} I & R_1 & R_2 & F_1 & F_2 & F_3 \\ \end{array} \\ \hline \begin{array}{c} I \\ R_1 \\ R_2 \\ F_1 \\ F_2 \\ F_3 \\ \end{array} & \begin{array}{cccccc} I & R_1 & R_2 & F_1 & F_2 & F_3 \\ R_1 & R_2 & I & F_2 & F_3 & F_1 \\ R_2 & I & R_1 & F_3 & F_1 & F_2 \\ F_1 & F_3 & F_2 & I & R_2 & R_1 \\ F_2 & F_1 & F_3 & R_1 & I & R_2 \\ F_3 & F_2 & F_1 & R_2 & R_1 & I \\ \end{array} \\ \end{array} \end{equation*}This group is non-abelian since, for example, \(F_1 F_2=R_2\) and \(F_2 F_1=R_1\text{.}\)
-
4! = 24, \(n!\text{.}\)
11.2.4.7.
11.3 Some General Properties of Groups
11.3.3 Exercises
11.3.3.1.
Answer.
-
\(f\) is injective:\begin{equation*} \begin{split} f(x) = f(y) & \Rightarrow a * x = a * y \\ & \Rightarrow x = y\textrm{ by left cancellation}\\ \end{split}\text{.} \end{equation*}\(f\) is surjective: For all \(b \in G\text{,}\) \(f(x) = b\) has the solution \(a^{-1}*b\text{.}\)
11.3.3.3.
Answer.
Induction: Assume that for some \(n \geq 2\text{,}\)
\begin{equation*}
\left(a_1*a_2* \cdots *a_n\right)^{-1}=a_n^{-1}* \cdots * a_2^{-1}*a_1^{-1}
\end{equation*}
We must show that
\begin{equation*}
\left(a_1*a_2* \cdots *a_n*a_{n+1}\right)^{-1}=a_{n+1}^{-1}*a_n^{-1}* \cdots * a_2^{-1}*a_1^{-1}
\end{equation*}
This can be accomplished as follows:
\begin{equation*}
\begin{split}
\left(a_1*a_2*\cdots *a_n*a_{n+1}\right)^{-1} &=\left(\left(a_1*a_2*\cdots *a_n\right)*a_{n+1}\right)^{-1}\textrm{
by the associative law}\\
&=a_{n+1}^{-1}*\left(a_1*a_2*\cdots *a_n\right)^{-1}\textrm{ by the basis}\\
&=a_{n+1}^{-1}*\left(a_n^{-1}*\cdots * a_2^{-1}*a_1^{-1}\right) \textrm{ by the induction hypothesis}\\
&= a_{n+1}^{-1}*a_n^{-1}*\cdots * a_2^{-1}*a_1^{-1} \textrm{ by the associative law}\\
\end{split}
\end{equation*}
11.3.3.5.
Answer.
In this answer, we will refer to Lemma 11.3.13 simply as “the lemma.”
-
Let \(p(n)\) be \(a^{-n}= \left(a^{-1}\right)^n\text{,}\) where \(a\) is any element of group \([G; *]\text{.}\) First we will prove that \(p(n)\) is true for all \(n \geq 0\text{.}\)Basis: If \(n = 0\text{,}\) Using the definition of the zero exponent, \(\left(a^0\right)^{-1} = e^{-1} = e\text{,}\) while \(\left(a^{-1}\right)^0= e\text{.}\) Therefore, \(p(0)\) is true.Induction: Assume that for some \(n \geq 0\text{,}\) \(p(n\)) is true.\begin{equation*} \begin{split} \left(a^{n+1}\right)^{-1} &= \left(a^n*a\right)^{-1}\textrm{ by the definition of exponentiation}\\ & =a^{-1}*\left(a^n\right)^{-1}\textrm{ by the lemma}\\ & = a^{-1}*\left(a^{-1}\right)^n\textrm{ by the induction hypothesis}\\ & = \left(a^{-1}\right)^{n+1} \textrm{ by the lemma} \end{split} \end{equation*}If \(n\) is negative, then \(-n\) is positive and\begin{equation*} \begin{split} a^{-n} & = \left(\left(\left(a^{-1}\right)^{-1}\right)^{-n} \right)\\ & =\left(a^{-1}\right)^{-(-n)}\textrm{ since the property is true for positive numbers}\\ & =\left(a^{-1}\right)^n \end{split} \end{equation*}
-
For \(m > 1\text{,}\) let \(p(m)\) be \(a^{n+m}=a^n*a^m\) for all \(n\geq 1\text{.}\) The basis for this proof follows directly from the basis for the definition of exponentiation.Induction: Assume that for some \(m > 1\text{,}\) \(p(m)\) is true. Then\begin{equation*} \begin{split} a^{n+(m+1)}&= a^{(n+m)+1}\textrm{ by the associativity of integer addition}\\ &=a^{n+m}*a^1\textrm{ by the definition of exponentiation}\\ &=\left(a^n*a^m\right)*a^1 \textrm{ by the induction hypothesis}\\ &= a^n*\left(a^m*a^1\right)\textrm{ by associativity}\\ &= a^n*a^{m+1}\textrm{ by the definition of exponentiation} \end{split} \end{equation*}To complete the proof, you need to consider the cases where \(m\) and/or \(n\) are negative.
-
Induction; Assume that \(p(m)\) is true for some \(m >\)0,\begin{equation*} \begin{split} \left(a^n\right)^{m+1}&=\left(a^n\right)^m*a^n \textrm{ by the definition of exponentiation}\\ &=a^{n m}*a^n\textrm{ by the induction hypothesis}\\ & =a^{n m + n}\textrm{ by part (b) of this proof}\\ & =a^{n(m+1)} \end{split} \end{equation*}Finally, if \(m\) is negative, we can verify that \(\left(a^n\right)^m= a^{n m}\) using many of the same steps as the positive case.
11.3.3.7.
Solution.
Note that \(0\) is an identity for the operation and that every element inverts itself. If \(\star\) were associative we would have the operation table of a group, but we don’t have a group, so the we can’t have associativity. One reason why the system isn’t a group is that the cancelation laws fail: \(4\star 1 = 4\star 3\) yet \(1 \neq 3\text{.}\)
11.4 Greatest Common Divisors and the Integers Modulo \(n\)
11.4.2 The Euclidean Algorithm
Investigation 11.4.1.
Solution.
If quotient in division is 1, then we get the slowest possible completion. If \(a = b + r\text{,}\) then working backwards, each remainder would be the sum of the two previous remainders. This described a sequence like the Fibonacci sequence and indeed, the greatest common divisor of two consecutive Fibonacci numbers will take the most steps to reach a final value of 1.
11.4.6 Exercises
11.4.6.1.
11.4.6.3.
11.4.6.5.
11.4.6.7.
11.4.6.9.
Solution.
-
The operation table can be created with SageMath:We know that multiplication mod 14 is associative, 1 is the identity and from the table we see that each element has an inverse in this system.
-
We know that multiplication mod \(n\) is associative, 1 is the identity and we are assuming that all element are invertible. In the next part we see that the invertable elements are exactly the set \(\mathbb{U}_{n}\text{.}\)
-
Let \(a\) be an element of \(\mathbb{Z}_{n}\) such that \(\gcd(n,a)=1\text{.}\) By Theorem 11.4.9 there exist integers \(s\) and \(t\) such that \(n s + a t = 1\text{.}\) By the division property, we can divide \(n\) into \(t\) to get \(t = n q + r\) where \(r \in \mathbb{Z}_{n}\text{.}\)\begin{equation*} n s + a t = 1 \Rightarrow a r = n(-(aq+s))+1 \Rightarrow a\times_{n} r=1 \end{equation*}Therefore, \(a\) has an inverse, and that inverse is in \(\mathbb{U}_{n}\text{.}\)
11.4.6.10.
11.4.6.11.
Solution.
The given conditions can be converted to a system of linear equations:
\begin{equation*}
\begin{array}{c}
f(1)=11 \Rightarrow a +_{17} b = 11\\
f(2)=4 \Rightarrow 2 \times_{17} a +_{17} b =4\\
\end{array}
\end{equation*}
If we subtract the first equation from the second, we get \(a = 4 +_{17} (-11) = 4 +_{17} 6= 10\text{.}\) This implies that \(b=1\text{,}\) and \(f(i) = 10\times+{17}i + 1\text{.}\) To get a formula for the inverse of \(f\) we solve \(f(j)=i\) for \(j\text{,}\) using the fact that the multiplicative inverse of 10 (mod 17) is 12.
\begin{equation*}
\begin{split}
f(j)=i & \Rightarrow 10\times+{17}j + 1 = i\\
& \Rightarrow 10\times+{17}j = i +_{17} 16\\
& \Rightarrow j = 12\times_{17}( i +_{17} 16)\\
\end{split}
\end{equation*}
Therefore \(f^{-1}(i) = 12\times_{17}( i +_{17} 16) = 12\times_{17} i +_{17} 5\text{.}\)
11.4.6.13.
Solution.
By Bézout’s lemma, \(450\) is an element of \(\mathbb{U}_{2021}\text{.}\) It’s inverse in the group is \(759\) because
\begin{equation*}
450 \cdot 759 = 2021\cdot 169 +1 \quad \Rightarrow \quad 450 \times_{2021} 759 =1.
\end{equation*}
11.4.6.15.
Solution.
There will always to two solutions, \(1\) and \(n-1\text{.}\) We can prove this as follows:
\begin{equation*}
\begin{split}
x^2=1 &\Leftrightarrow x^1-1 \equiv_{p} 0\\
& \Leftrightarrow p \mid (x^2-1)\\
& \Leftrightarrow p \mid (x-1)(x+1)\\
& \Leftrightarrow p \mid (x-1) \textrm{ or }p \mid (x+1)\\
& \Leftrightarrow x \equiv_{p} 1 \textrm{ or }x \equiv_p -1\\
& \Leftrightarrow x=1 \textrm{ or }x=p-1
\end{split}
\end{equation*}
The fourth step applies a theorem that follows from Bézout’s lemma that states that if a prime divides evenly into a product, then it must divide into one of the factors.
11.4.6.17.
Answer.
There are several possible reasons that can be cited. Here is one for each part.
-
The operation \(+_4\) isn’t a valid binary operation on \(\mathbb{Z}_3\) since \(1+_4 2 =3 \not\in \mathbb{Z}_3\text{.}\)
11.5 Subsystems
11.5.5 Exercises
11.5.5.1.
11.5.5.3.
11.5.5.5.
Answer.
-
\(\langle 1\rangle = \langle 5\rangle = \mathbb{Z}_6\text{,}\) \(\quad\)\(\langle 2\rangle = \langle 4\rangle = \{2, 4, 0\}\text{,}\) \(\langle 3\rangle = \{3, 0\}\text{,}\) \(\langle 0\rangle = \{0\}\)
-
\(\langle 1\rangle = \langle 5\rangle = \langle 7\rangle = \langle 11\rangle =\mathbb{Z}_{12}\text{,}\) \(\langle 2\rangle = \langle 10\rangle = \{2, 4, 6, 8, 10, 0\}\text{,}\) \(\langle 3\rangle = \langle 9\rangle = \{3, 6, 9, 0\}\text{,}\) \(\langle 4\rangle = \langle 8 \rangle = \{ 4 , 8, 0\}\text{,}\) \(\langle 6\rangle = \{6, 0\}\text{,}\) \(\langle 0\rangle = \{0\}\)
-
\(\langle 1\rangle = \langle 3\rangle = \langle 5 \rangle = \langle 7\rangle = \mathbb{Z}_8\text{,}\) \(\langle 2\rangle = \langle 6\rangle = \{2, 4, 6, 0\}\text{,}\) \(\langle 4\rangle = \{4, 0\}\text{,}\) \(\langle 0\rangle = \{0\}\)
-
Based on the ordering diagrams for parts a through c in Figure 11.5.13, we would expect to see an ordering diagram similar to the one for divides on \(\{1, 2, 3, 4, 6, 8, 12, 24\}\) (the divisors of 24) if we were to examine the subgroups of \(\mathbb{Z}_{24}\text{.}\) This is indeed the case.
Figure for exercise 5 of Section 11.5
11.5.5.7.
Answer.
Assume that \(H\) and \(K\) are subgroups of group \(G\text{,}\) and that, as in Figure 11.5.12, there are elements \(x \in H - K\) and \(y \in K - H\text{.}\) Consider the product \(x * y\text{.}\) Where could it be placed in the Venn diagram? If we can prove that it must lie in the outer region, \(H^c \cap K^c=(H \cup K)^c\text{,}\) then we have proven that \(H \cup K\) is not closed under \(*\) and cannot be a subgroup of \(G\text{,}\) Assume that \(x*y\in H\text{.}\) Since \(x\) is in \(H\text{,}\) \(x^{-1}\) is in \(H\) and so by closure \(x^{-1}*(x * y )= y \in H\) which is a contradiction. Similarly, \(x*y \notin K\text{.}\)
One way to interpret this theorem is that no group is the union of two groups.
11.6 Direct Products
11.6.3 Exercises
11.6.3.1.
Answer.
Table of \(\mathbb{Z}_2\times \mathbb{Z}_3\text{:}\)
\begin{equation*}
\begin{array}{c|cccccc}
+&(0,0)&(0,1)&(0,2)&(1,0)&(1,1)&(1,2)\\
\hline
(0,0)&(0,0)&(0,1)&(0,2)&(1,0)&(1,1)&(1,2)\\
(0,1)&(0,1)&(0,2)&(0,0)&(1,1)&(1,2)&(1,0)\\
(0,2)&(0,2)&(0,0)&(0,1)&(1,2)&(1,0)&(1,1)\\
(1,0)&(1,0)&(1,1)&(1,2)&(0,0)&(0,1)&(0,2)\\
(1,1)&(1,1)&(1,2)&(1,0)&(0,1)&(0,2)&(0,0)\\
(1,2)&(1,2)&(1,0)&(1,1)&(0,2)&(0,0)&(0,1)
\end{array}
\end{equation*}
The only two proper subgroups are \(\{(0, 0), (1, 0)\}\) and \(\{(0, 0), (0, 1), (0, 2)\}\)
11.6.3.3. Algebraic properties of the \(n\)-cube.
Answer.
-
(i) \(a + b \textrm{ could be }(1, 0) \textrm{ or } (0, 1)\text{.}\) (ii) \(a + b = (1, 1)\text{.}\)
-
(i) \(a + b \textrm{ could be}(1, 0, 0), (0, 1, 0), \textrm{ or }(0, 0, 1)\text{.}\) (ii) \(a + b = (1, 1, 1)\text{.}\)
11.6.3.5.
11.7 Isomorphisms
11.7.4 Exercises
11.7.4.1.
Answer.
-
No, \(\mathbb{Z}_2\times \mathbb{Z}\) has a two element subgroup while \(\mathbb{Z} \times \mathbb{Z}\) does not.
-
No. \(\mathbb{Q} \times \mathbb{Q}\) is countable and \(\mathbb{R}\) is not. Therefore, no bijection can exist between them.
-
Yes.
-
No.
-
Yes, one isomorphism is defined by \(f\left(a_1, a_2,a_3,a_4\right)=\left( \begin{array}{cc} a_1 & a_2 \\ a_3 & a_4 \\ \end{array} \right)\text{.}\)
-
Yes, one isomorphism is defined by \(f\left(a_1,a_2\right)=\left(a_1,10^{a_2}\right)\text{.}\)
-
Yes.
-
Yes \(f(k) = k(1,1)\text{.}\)
11.7.4.3.
Answer.
Consider three groups \(G_1\text{,}\) \(G_2\text{,}\) and \(G_3\) with operations \(*, \diamond , \textrm{ and } \star \text{,}\) respectively. We want to show that if \(G_1\) is isomorphic to \(G_2\text{,}\) and if \(G_2\) is isomorphic to \(G_3\) , then \(G_1\) is isomorphic to \(G_3\text{.}\)
\begin{equation*}
G_1 \textrm{ isomorphic} \textrm{ to } G_2\Rightarrow \textrm{ there} \textrm{ exists} \textrm{ an} \textrm{ isomorphism } f:G_1\to G_2
\end{equation*}
\begin{equation*}
G_2 \textrm{ isomorphic} \textrm{ to } G_3\Rightarrow \textrm{ there} \textrm{ exists} \textrm{ an} \textrm{ isomorphism } g:G_2\to G_3
\end{equation*}
If we compose \(g\) with \(f\text{,}\) we get the function \(g\circ f:G_1\to G_3\text{,}\) By Theorem 7.3.6 and Theorem 7.3.7, \(g\circ f\) is a bijection, and if \(a,b\in G_1\text{,}\)
\begin{equation*}
\begin{split}
(g\circ f)(a*b) &=g(f(a*b))\\
&=g(f(a)\diamond f(b))\quad \textrm{ since } f \textrm{ is an isomorphism}\\
& =g(f(a))\star g(f(b))\quad \textrm{ since } g \textrm{ is an isomorphism}\\
& =(g\circ f)(a) \star (g\circ f)(b)
\end{split}
\end{equation*}
Therefore, \(g\circ f\) is an isomorphism from \(G_1\) into \(G_3\text{,}\) proving that “is isomorphic to” is transitive.
11.7.4.5.
Answer.
By Theorem 11.7.14(a), \(T(0)\) must be 1. \(T(2)=T(1+_4 1)=T(1)\times_5 T(1) = 3 \times_5 3 = 4\text{.}\) Since \(T\) is a bijection, \(T(3)=2\text{.}\)
11.7.4.7.
Answer.
Let \(G\) be an infinite cyclic group generated by \(a\text{.}\) Then, using multiplicative notation, \(G=\left\{\left.a^n\right| n\in \mathbb{Z}\right\}\text{.}\) The map \(T: G \rightarrow \mathbb{Z}\) defined by \(T\left(a^n\right)=n\) is an isomorphism. This is indeed a function, since \(a^n=a^m\) implies \(n =m\text{.}\) Otherwise, \(a\) would have a finite order and would not generate \(G\text{.}\)
-
\(T\) is one-to-one, since \(T\left(a^n\right) = T\left(a^m\right)\) implies \(n = m\text{,}\) so \(a^n= a^m\text{.}\)
-
\(\displaystyle T\left(a^n*a^m \right) = T\left(a^{n+m}\right) =n + m\ =T\left(a^n\right)+T\left(a^m\right)\)
11.7.4.11.
11.7.4.13.
12 More Matrix Algebra
12.1 Systems of Linear Equations
12.1.7 Exercises
12.1.7.1.
12.1.7.3.
Answer.
-
Basic variables: \(x_1\text{,}\) \(x_2\) and \(x_4\text{.}\) Free variable: \(x_3\text{.}\) Solution set: \(\{(1.2+5x_3, 2.6-4 x_3, 4.5) \mid x_3 \in \mathbb{R}\}\)
-
Basic variables: \(x_1\) and \(x_2\text{.}\) Free variable: \(x_3\text{.}\) The solution set is empty because the last row of the matrix converts to the inconsistent equation \(0=1\text{.}\)
-
Basic variables: \(x_1\) and \(x_2\text{.}\) Free variable: \(x_3\text{.}\) Solution set: \(\left\{\left(-6 x_3 + 5, 2 x_3+1, x_3 \right) \mid x_3 \in \mathbb{R}\right\}\)
-
Basic variables: \(x_1\text{,}\) \(x_2\) and \(x_3\text{.}\) Free variable: \(x_4\text{.}\) Solution set: \(\left\{\left(3 x_4 + 1, -2x_4 + 2, x_4 + 1, x_4\right) \mid x_4 \in \mathbb{R}\right\}\)
12.1.7.5.
12.2 Matrix Inversion
12.2.3 Exercises
12.2.3.3.
Answer.
-
\(\displaystyle \left( \begin{array}{cc} \frac{15}{11} & \frac{30}{11} \\ \frac{3}{11} & -\frac{5}{11} \\ \end{array} \right)\)
-
\(\displaystyle \left( \begin{array}{ccc|c} -20 & \frac{21}{2} & \frac{9}{2} & -\frac{3}{2} \\ 2 & -1 & 0 & 0 \\ -4 & 2 & 1 & 0 \\ 7 & -\frac{7}{2} & -\frac{3}{2} & \frac{1}{2} \\ \end{array} \right)\)
-
The inverse does not exist. When the augmented matrix is row-reduced (see below), the last row of the first half cannot be manipulated to match the identity matrix.
-
\(\displaystyle \left( \begin{array}{ccc} 1 & 0 & 0 \\ -3 & 1 & 1 \\ -4 & 1 & 2 \\ \end{array} \right)\)
-
The inverse does not exist.
-
\(\displaystyle \left( \begin{array}{ccc} 9 & -36 & 30 \\ -36 & 192 & -180 \\ 30 & -180 & 180 \\ \end{array} \right)\)
12.2.3.5.
Answer.
The solutions are in the solution section of Section 12.1, exercise 1, We illustrate with the outline of the solution to part (c). The matrix version of the system is
\begin{equation*}
\left(
\begin{array}{ccc}
1 & 1 & 2 \\
1 & 2 & -1 \\
1 & 3 & 1 \\
\end{array}
\right)\left(
\begin{array}{c}
x_1 \\
x_2 \\
x_3 \\
\end{array}
\right)=\left(
\begin{array}{c}
1 \\
-1 \\
5 \\
\end{array}
\right)
\end{equation*}
We compute the inverse of the matrix of coefficients and get
\begin{equation*}
A^{-1}=\left(
\begin{array}{ccc}
1 & 1 & 2 \\
1 & 2 & -1 \\
1 & 3 & 1 \\
\end{array}
\right)^{-1}=\frac{1}{5}\left(
\begin{array}{ccc}
5 & 5 & -5 \\
-2 & -1 & 3 \\
1 & -2 & 1 \\
\end{array}
\right)
\end{equation*}
and
\begin{equation*}
\left(
\begin{array}{c}
x_1 \\
x_2 \\
x_3 \\
\end{array}
\right)=A^{-1}\left(
\begin{array}{c}
1 \\
-1 \\
5 \\
\end{array}
\right)=\left(
\begin{array}{c}
-5 \\
\frac{14}{5} \\
\frac{8}{5} \\
\end{array}
\right)
\end{equation*}
12.3 An Introduction to Vector Spaces
12.3.3 Exercises
12.3.3.3.
Answer.
The dimension of \(M_{2\times 3}(\mathbb{R})\) is 6 and yes, \(M_{m\times n}(\mathbb{R})\) is also a vector space of dimension \(m \cdot n\text{.}\) One basis for \(M_{m\times n}(\mathbb{R})\) is \(\{A_{ij} \mid 1 \leq i \leq m, 1 \leq j \leq n\}\) where \(A_{ij}\) is the \(m\times n\) matrix with entries all equal to zero except for in row \(i\text{,}\) column \(j\) where the entry is 1.
12.3.3.5.
Solution.
Let \(p(x), q(x) \in P^3\) and \(\alpha, \beta \in \mathbb{R}\text{,}\) where
\begin{equation*}
p(x) = a_0 + a_1x + a_2x^2 + a_3x^3, \quad q(x) = b_0 + b_1x + b_2x^2 + b_3x^3.
\end{equation*}
-
Closure under addition:\begin{equation*} p(x) + q(x) = (a_0 + b_0) + (a_1 + b_1)x + (a_2 + b_2)x^2 + (a_3 + b_3)x^3 \in V. \end{equation*}
-
Associativity of addition:For any \(r(x) \in V\text{,}\)\begin{equation*} (p(x) + q(x)) + r(x) = p(x) + (q(x) + r(x)). \end{equation*}
-
Existence of additive identity in \(P^3\text{:}\)Let \(0(x) = 0 + 0x + 0x^2 + 0x^3 \in V\text{,}\) then\begin{equation*} p(x) + 0(x) = p(x). \end{equation*}
-
Existence of additive inverses in \(P^3\text{:}\)Let \(-p(x) = -a_0 - a_1x - a_2x^2 - a_3x^3 \in P^3\text{,}\) then\begin{equation*} p(x) + (-p(x)) = 0(x). \end{equation*}
-
Closure under scalar multiplication:\begin{equation*} \alpha \cdot p(x) = \alpha a_0 + \alpha a_1 x + \alpha a_2 x^2 + \alpha a_3 x^3 \in P^3. \end{equation*}
-
Distributivity of scalar multiplication over vector addition:\begin{equation*} \alpha(p(x) + q(x)) = \alpha p(x) + \alpha q(x). \end{equation*}
-
Distributivity of scalar multiplication over scalar addition:\begin{equation*} (\alpha + \beta)p(x) = \alpha p(x) + \beta p(x). \end{equation*}
-
Associativity of scalar multiplication:\begin{equation*} \alpha(\beta p(x)) = (\alpha \beta) p(x). \end{equation*}
Conclusion: All vector space axioms are satisfied, so we conclude that: \(P^3\) is a vector space over \(\mathbb{R}\) with dimension 4, because the set of vectors \(\{1,x,x^2,x^3\}\) forms a basis for the space.
12.3.3.7.
12.3.3.9.
Answer.
-
If \(x_1 = (1, 0)\text{,}\) \(x_2= (0, 1)\text{,}\) and \(y = \left(b_1, b_2\right)\text{,}\) then \(y = b_1x_1+b_2x_2\text{.}\) If \(x_1 = (3, 2)\text{,}\) \(x_2= (2,1)\text{,}\) and \(y = \left(b_1, b_2\right)\text{,}\) then \(y =\left(- b_1+2b_2\right)x_1+\left(2b_1-3b_2\right)x_2\text{.}\)
-
If \(y = \left(b_1, b_2\right)\) is any vector in \(\mathbb{R}^2\) , then \(y =\left(- 3b_1+4b_2\right)x_1+\left(-b_1+b_2\right)x_2 + (0)x_3\)
-
2, \(n\)
-
\(\displaystyle \left( \begin{array}{cc} x & y \\ z & w \\ \end{array} \right)= x A_1+y A_2+ z A_3+ w A_4\)
-
\(a_0+a_1x + a_2x^2+ a_3x^3=a_0(1)+a_1(x) + a_2\left(x^2\right)+ a_3\left(x^3\right)\text{.}\)
12.3.3.11.
Answer.
-
The set is linearly independent: let \(a\) and \(b\) be scalars such that \(a(4, 1) + b(1, 3) = (0, 0)\text{,}\) then \(4a + b = 0\textrm{ and } a + 3b= 0\) which has \(a = b = 0\) as its only solutions. The set generates all of \(\mathbb{R}^2\text{:}\) let \((a, b)\) be an arbitrary vector in \(\mathbb{R}^2\) . We want to show that we can always find scalars \(\beta _1\) and \(\beta _2\) such that \(\beta _1(4, 1) +\beta _2 (1,3) = (a, b)\text{.}\) This is equivalent to finding scalars such that \(4\beta _1 +\beta _2 = a\) and \(\beta _1 + 3\beta _2 = b\text{.}\) This system has a unique solution \(\beta _1=\frac{3a - b}{11}\text{,}\) and \(\beta _2= \frac{4b-a}{11}\text{.}\) Therefore, the set generates \(\mathbb{R}^2\text{.}\)
12.3.3.13.
Answer.
The answer to the last part is that the three vector spaces are all isomorphic to one another. Once you have completed part (a) of this exercise, the following translation rules will give you the answer to parts (b) and (c),
\begin{equation*}
(a,b,c,d) \leftrightarrow \left(
\begin{array}{cc}
a & b \\
c & d \\
\end{array}
\right)\leftrightarrow a + b x+c x^2+ d x^2
\end{equation*}
12.4 The Diagonalization Process
12.4.4 Exercises
12.4.4.1.
Answer.
-
Any nonzero multiple of \(\left( \begin{array}{c} 1 \\ -1 \\ \end{array} \right)\) is an eigenvector associated with \(\lambda =1\text{.}\)
-
Any nonzero multiple of \(\left( \begin{array}{c} 1 \\ 2 \\ \end{array} \right)\) is an eigenvector associated with \(\lambda =4\text{.}\)
-
Let \(x_1=\left( \begin{array}{c} a \\ -a \\ \end{array} \right)\) and \(x_2=\left( \begin{array}{c} b \\ 2b \\ \end{array} \right)\) . You can verify that \(c_1x_1+ c_2x_2=\left( \begin{array}{c} 0 \\ 0 \\ \end{array} \right)\) if and only if \(c_1= c_2= 0.\) Therefore, \(\left\{x_1,x_2\right\}\) is linearly independent.
12.4.4.3.
12.4.4.5.
Answer.
-
If \(P=\left( \begin{array}{cc} 2 & 1 \\ 3 & -1 \\ \end{array} \right)\text{,}\) then \(P^{-1}A P=\left( \begin{array}{cc} 4 & 0 \\ 0 & -1 \\ \end{array} \right)\text{.}\)
-
If \(P=\left( \begin{array}{cc} 1 & 1 \\ 7 & 1 \\ \end{array} \right)\text{,}\) then \(P^{-1}A P=\left( \begin{array}{cc} 5 & 0 \\ 0 & -1 \\ \end{array} \right)\text{.}\)
-
If \(P=\left( \begin{array}{cc} 1 & 0 \\ 0 & 1 \\ \end{array} \right)\text{,}\) then \(P^{-1}A P=\left( \begin{array}{cc} 3 & 0 \\ 0 & 4 \\ \end{array} \right)\text{.}\)
-
If \(P=\left( \begin{array}{ccc} 1 & -1 & 1 \\ -1 & 4 & 2 \\ -1 & 1 & 1 \\ \end{array} \right)\text{,}\) then \(P^{-1}A P=\left( \begin{array}{ccc} -2 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \\ \end{array} \right)\text{.}\)
-
\(A\) is not diagonalizable. Five is a double root of the characteristic equation, but has an eigenspace with dimension only 1.
-
We are given the symmetric matrix in 5(f)\begin{equation*} A = \begin{bmatrix} 1 & -1 & 0 \\ -1 & 2 & -1 \\ 0 & -1 & 1 \end{bmatrix}. \end{equation*}Step 1: Find the characteristic polynomial.We compute \(\det(A - \lambda I)\text{,}\) where\begin{equation*} A - \lambda I = \begin{bmatrix} 1 - \lambda & -1 & 0 \\ -1 & 2 - \lambda & -1 \\ 0 & -1 & 1 - \lambda \end{bmatrix}. \end{equation*}We compute the determinant:\begin{equation*} \det(A - \lambda I) = (1 - \lambda) \begin{vmatrix} 2 - \lambda & -1 \\ -1 & 1 - \lambda \end{vmatrix} - (-1) \begin{vmatrix} -1 & -1 \\ 0 & 1 - \lambda \end{vmatrix}. \end{equation*}Compute the 2×2 minors:\begin{equation*} = (1 - \lambda)\left[(2 - \lambda)(1 - \lambda) - (-1)(-1)\right] + \left[(-1)(1 - \lambda) - (0)(-1)\right] \end{equation*}\begin{equation*} = (1 - \lambda)\left[(2 - \lambda)(1 - \lambda) - 1\right] - (1 - \lambda). \end{equation*}Now simplify:\begin{equation*} (2 - \lambda)(1 - \lambda) = 2 - 3\lambda + \lambda^2, \end{equation*}so:\begin{equation*} = (1 - \lambda)(\lambda^2 - 3\lambda + 1) - (1 - \lambda) = (1 - \lambda)(\lambda^2 - 3\lambda + 1 - 1) = (1 - \lambda)(\lambda^2 - 3\lambda). \end{equation*}Thus, the characteristic polynomial is:\begin{equation*} \lambda(\lambda - 1)(\lambda - 3), \end{equation*}and the eigenvalues are:\begin{equation*} \lambda_1 = 0, \quad \lambda_2 = 1, \quad \lambda_3 = 3. \end{equation*}Step 2: Find eigenvectors.
-
For \(\lambda = 0\text{,}\) solve \(A\vec{v} = 0\text{:}\)\begin{equation*} \begin{bmatrix} 1 & -1 & 0 \\ -1 & 2 & -1 \\ 0 & -1 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ 0 \end{bmatrix} \Rightarrow \vec{v}_0 = \begin{bmatrix} 1 \\ 2 \\ 1 \end{bmatrix}. \end{equation*}
-
For \(\lambda = 1\text{,}\) solve \((A - I)\vec{v} = 0\text{:}\)\begin{equation*} \begin{bmatrix} 0 & -1 & 0 \\ -1 & 1 & -1 \\ 0 & -1 & 0 \end{bmatrix} \Rightarrow \vec{v}_1 = \begin{bmatrix} 1 \\ 0 \\ -1 \end{bmatrix}. \end{equation*}
-
For \(\lambda = 3\text{,}\) solve \((A - 3I)\vec{v} = 0\text{:}\)\begin{equation*} \begin{bmatrix} -2 & -1 & 0 \\ -1 & -1 & -1 \\ 0 & -1 & -2 \end{bmatrix} \Rightarrow \vec{v}_3 = \begin{bmatrix} 1 \\ -2 \\ 1 \end{bmatrix}. \end{equation*}
Step 3: Form the diagonalization.Let\begin{equation*} P = \begin{bmatrix} 1 & 1 & 1 \\ 2 & 0 & -2 \\ 1 & -1 & 1 \end{bmatrix}, \quad D = \begin{bmatrix} 0 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 3 \end{bmatrix}. \end{equation*} -
12.4.4.7.
Answer.
This is a direct application of the definition of matrix multiplication. Let \(A_{(i)}\) be the \(i^{\textrm{th}}\) row of \(A\text{,}\) and let \(P^{(j)}\) be the \(j^{\textrm{th}}\) column of \(P\text{.}\) Then the \(j^{\textrm{th}}\) column of the product \(A P\) is
\begin{equation*}
\left(
\begin{array}{c}
A_{(1)}P^{(j)} \\
A_{(2)}P^{(j)} \\
\vdots \\
A_{(n)}P^{(j)} \\
\end{array}
\right)
\end{equation*}
Hence, \((AP)^{(j)}= A\left(P^{(j)}\right)\) for \(j =1,2,\ldots , n\text{.}\) Thus, each column of \(A P\) depends on \(A\) and the \(j^{\textrm{ th}}\) column of \(P\text{.}\)
12.5 Some Applications
12.5.5 Exercises
12.5.5.4.
12.5.5.5.
Answer.
-
Since \(A=A^1= \left( \begin{array}{ccc} 1 & 1 & 0 \\ 1 & 0 & 1 \\ 0 & 1 & 1 \\ \end{array} \right)\text{,}\) there are 0 paths of length 1 from: node c to node a, node b to node b, and node a to node c; and there is 1 path of length 1 for every other pair of nodes.
-
The characteristic polynomial is \(\lvert A-c I\rvert = \left| \begin{array}{ccc} 1-c & 1 & 0 \\ 1 & -c & 1 \\ 0 & 1 & 1-c \\ \end{array} \right| = -c^3+2 c^2+c-2\)Solving the characteristic equation \(-c^3+2 c^2+c-2=0\) we find solutions 1, 2, and -1.If \(c=1\text{,}\) we find the associated eigenvector by finding a nonzero solution to \(\left( \begin{array}{ccc} 0 & 1 & 0 \\ 1 & -1 & 1 \\ 0 & 1 & 0 \\ \end{array} \right)\left( \begin{array}{c} x_1 \\ x_2 \\ x_3 \\ \end{array} \right)=\left( \begin{array}{c} 0 \\ 0 \\ 0 \\ \end{array} \right)\) One of these, which will be the first column of \(P\text{,}\) is \(\left( \begin{array}{c} 1 \\ 0 \\ -1 \\ \end{array} \right)\)If \(c=2\text{,}\) the system \(\left( \begin{array}{ccc} -1 & 1 & 0 \\ 1 & -2 & 1 \\ 0 & 1 & -1 \\ \end{array} \right)\left( \begin{array}{c} x_1 \\ x_2 \\ x_3 \\ \end{array} \right)=\left( \begin{array}{c} 0 \\ 0 \\ 0 \\ \end{array} \right)\) yields eigenvectors, including \(\left( \begin{array}{c} 1 \\ 1 \\ 1 \\ \end{array} \right)\text{,}\) which will be the second column of \(P\text{.}\)If \(c = -1\text{,}\) then the system determining the eigenvectors is \(\left( \begin{array}{ccc} 2 & 1 & 0 \\ 1 & 1 & 1 \\ 0 & 1 & 2 \\ \end{array} \right)\left( \begin{array}{c} x_1 \\ x_2 \\ x_3 \\ \end{array} \right)=\left( \begin{array}{c} 0 \\ 0 \\ 0 \\ \end{array} \right)\) and we can select \(\left( \begin{array}{c} 1 \\ -2 \\ 1 \\ \end{array} \right)\text{,}\) although any nonzero multiple of this vector could be the third column of \(P\text{.}\)
-
Assembling the results of part (b) we have \(P=\left( \begin{array}{ccc} 1 & 1 & 1 \\ 0 & 1 & -2 \\ -1 & 1 & 1 \\ \end{array} \right)\) .\begin{equation*} \begin{split} A^4 & = P \left( \begin{array}{ccc} 1^4 & 0 & 0 \\ 0 & 2^4 & 0 \\ 0 & 0 & (-1)^{4 } \\ \end{array} \right)P^{-1}= P \left( \begin{array}{ccc} 1 & 0 & 0 \\ 0 & 16 & 0 \\ 0 & 0 & 1 \\ \end{array} \right)P^{-1}\\ &=\left( \begin{array}{ccc} 1 & 16 & 1 \\ 0 & 16 & -2 \\ -1 & 16 & 1 \\ \end{array} \right)\left( \begin{array}{ccc} \frac{1}{2} & 0 & -\frac{1}{2} \\ \frac{1}{3} & \frac{1}{3} & \frac{1}{3} \\ \frac{1}{6} & -\frac{1}{3} & \frac{1}{6} \\ \end{array} \right)\\ &=\left( \begin{array}{ccc} 6 & 5 & 5 \\ 5 & 6 & 5 \\ 5 & 5 & 6 \\ \end{array} \right)\\ \end{split} \end{equation*}Hence there are five different paths of length 4 between distinct vertices, and six different paths that start and end at the same vertex. The reader can verify these facts from Figure 12.5.4
12.5.5.7.
Answer.
-
\(e^A=\left( \begin{array}{cc} e & e \\ 0 & 0 \\ \end{array} \right)\) , \(e^B=\left( \begin{array}{cc} 0 & 0 \\ 0 & e^2 \\ \end{array} \right)\text{,}\) and \(e^{A+B}=\left( \begin{array}{cc} e & e^2-e \\ 0 & e^2 \\ \end{array} \right)\)
-
Let \(\pmb{0}\) be the zero matrix, \(e^{\pmb{0}}=I + \pmb{0}+\frac{\pmb{0}^2}{2}+\frac{\pmb{0}^3}{6}+\ldots =I\) .
-
Assume that \(A\) and \(B\) commute. We will examine the first few terms in the product \(e^A e^B\text{.}\) The pattern that is established does continue in general. In what follows, it is important that \(A B = B A\text{.}\) For example, in the last step, \((A+B)^2\) expands to \(A^2+A B + B A + B^2\text{,}\) not \(A^2+ 2 A B + B^2\text{,}\) if we can’t assume commutativity.\begin{equation*} \begin{split} e^Ae^B &= \left(\sum _{k=0}^{\infty } \frac{A^k}{k!}\right) \left(\sum _{k=0}^{\infty } \frac{B^k}{k!}\right)\\ & =\left(I + A+\frac{A^2}{2}+ \frac{A^3}{6}+ \cdots \right)\left(I +B+\frac{B^2}{2}+ \frac{B^3}{6}+ \cdots \right)\\ &= I + A + B+ \frac{A^2}{2}+ A B + \frac{B^2}{2}+\frac{A^3}{6}+ \frac{A^2B}{2}+\frac{A B^2}{2}+ \frac{B^3}{6}+\cdots \\ &= I + (A+B) + \frac{1}{2}\left(A^2+ 2 A B + B^2\right)+ \frac{1}{6}\left(A^3+ 3A^2B+ 3A B^2+ B^3\right)+\cdots \\ &=I + (A+B)+ \frac{1}{2}(A+B)^2+ \frac{1}{6}(A+B)^3+\cdots \\ & =e^{A+B}\\ \end{split} \end{equation*}
-
Since \(A\) and \(-A\) commute, we can apply part d;\begin{equation*} e^Ae^{-A} = e^{A+(-A)} =e^{\pmb{0}} =I \end{equation*}
12.6 Linear Equations over the Integers Mod 2
12.6.2 Exercises
12.6.2.1.
12.6.2.2.
Answer.
As suggested here is the augmented matrix with both right sides, and its row reduction:
\begin{equation*}
\begin{split}
\left(
\begin{array}{cccc|cc}
1 & 1 & 0 & 1 & 1 & 1 \\
1 & 0 & 1 & 1 & 0 & 0 \\
0 & 1 & 1 & 0 & 1 & 0 \\
\end{array}
\right) & \text{ }\longrightarrow \text{ }
\left(
\begin{array}{cccc|cc}
\textbf{1} & 0 & 1 & 1 & 0 & 0 \\
0 & \textbf{1} & 1 & 0 & 1 & 0 \\
0 & 0 & 0 & 0 & 0 & 1 \\
\end{array}
\right)\\
\end{split}
\end{equation*}
There are only two basic variables here because the left side of the last equation is the sum of the left sides of the first two equations.
-
Ignoring the last column of both matrices, we see that the last equation of the first system reduces to \(0=0\text{,}\) which is always true, and the first two equations yield two free variables, \(x_3\) and \(x_4\text{.}\) The general solution is the set of quadruples \(\{(x_3 +_2 x_4,x_3 +_2 1, x_3, x_4) \mid x_3, x_4 \in \mathbb{Z}_2 \}\text{.}\) The cardinality of the solution set is 4.
-
If we replace the fifth column with the sixth one, the last row indicates that \(0=1\text{,}\) which means that the solution set is empty.
12.6.2.3.
Answer.
-
Row reduction produces a solution with one free variable, \(x_3\text{.}\)\begin{equation*} \begin{split} (x_1, x_2, x_3, x_4, x_5)& =(x_3,x_3,x_3,0,0)\\ & = x_3 (1,1,1,0,0) \\ \end{split} \end{equation*}The solution set has only two elements. It is \(\{(0,0,0,0,0), (1,1,1,0,0)\}\text{.}\) Since \(\mathbb{Z}_{2}^{5}\) is a finite group, the solution set is a subgroup because it is closed with respect to coordinatewise mod 2 addition.
-
The row-reduced augmented matrix of coefficients provides the solution\begin{equation*} \begin{split} (x_1, x_2, x_3, x_4, x_5)& =(x_3,1+x_3,x_3,1,0)\\ & = (0,1,0,1,0) + x_3 (1,1,1,0,0) \\ \end{split} \end{equation*}Therefore, the solution to this system is a shift of the solution set to the homogeneous system by the vector \((0,1,0,1,0)\text{,}\) which is \(\{(0,1,0,1,0), (1,0,1,1,0)\}\)
13 Boolean Algebra
13.1 Posets Revisited
Exercises
13.1.1.
13.1.3.
Answer.
-
Solution for Hasse diagram (b):
-
\begin{equation*} \begin{array}{c|c} \begin{array}{c|ccccc} \lor &a_1 & a_2 & a_3 & a_4 & a_5 \\ \hline a_1 & a_1 &a_2 & a_3 & a_4 & a_5 \\ a_2 & a_2 & a_2 & a_4 & a_4 & a_5 \\ a_3 &a_3 & a_4 & a_3 & a_4 & a_5 \\ a_4 & a_4 & a_4 & a_4 & a_4 & a_5 \\ a_5 & a_5 & a_5 & a_5 & a_5 & a_5 \\ \end{array} &\quad \begin{array}{c|ccccc} \land & a_1 & a_2 & a_3 & a_4 & a_5 \\\hline a_1 & a_1 & a_1 & a_1 & a_1 & a_1 \\ a_2 & a_1 & a_2 & a_1 & a_2 & a_2 \\ a_3 & a_1 & a_1 & a_3 & a_3 & a_3 \\ a_4 & a_1 & a_2 & a_3 & a_4 & a_4 \\ a_5 & a_1 & a_2 & a_3 & a_4 & a_5 \\ \end{array} \end{array} \end{equation*}
-
-
Partial solution for Hasse diagram (f):
-
No greatest element exists, but \(a_1\) is the least element.
13.1.5.
Answer.
If \(0\) and \(0'\) are distinct least elements, then
\begin{equation*}
\left.
\begin{array}{cc}
0\leq 0' & \textrm{ since } 0 \textrm{ is a least element} \\
0'\leq 0 & \textrm{ since } 0' \textrm{ is a least element} \\
\end{array}
\right\}\Rightarrow 0=0' \textrm{ by antisymmetry, a contradiction}
\end{equation*}
13.1.7.
Answer.
-
The sum of elements in \(A \cap B =\{2,3,6\}\) is odd and disqualifies the set from being an element of the poset.
-
The following correctly complete the statements in this part.
-
Any set that contains the union of \(A\cup B=\{1,2,3,6,7\}\) but also contains 3 or 5, but not both will be an upper bound. You can create several by including on not including 4 or 8.
-
The least upper bound doesn’t exist. Notice that the union of \(A\) and \(B\) isn’t in \(\mathcal{P}_0\text{.}\) One of the two sets \(\{1,2,3,5,6,7\}\) and \(\{1,2,3,6,7,9\}\) is contained within every upper bound of \(A\) and \(B\) but neither is contained within the other.
13.2 Lattices
Exercises
13.2.5.
13.3 Boolean Algebras
Exercises
13.3.1.
Answer.
\(\begin{array}{cc}
B & \textrm{ Complement of } B \\
\hline
\begin{array}{c}
\emptyset \\
\{a\} \\
\{b\} \\
\{c\} \\
\{a,b\} \\
\{a,c\} \\
\{b,c\} \\
A \\
\end{array}
&
\begin{array}{c}
A \\
\{b,c\} \\
\{a,c\} \\
\{a,b\} \\
\{c\} \\
\{b\} \\
\{a\} \\
\emptyset \\
\end{array}
\\
\end{array}\)
This lattice is a Boolean algebra since it is a distributive complemented lattice.
13.3.3.
13.3.5.
Answer.
-
\(\displaystyle S^*:a \lor b= a \textrm{ if } a \geq b\)
-
The dual of \(S:A\cap B = A\textrm{ if }A \subseteq B\) is \(S^*:A \cup B = A\textrm{ if } A \supseteq B\)
-
Yes
-
The dual of \(S:p \land q\Leftrightarrow p\textrm{ }\textrm{ if } p\Rightarrow q\) is \(S^*:p \lor q\Leftrightarrow p \textrm{ if } q\Rightarrow p\)
-
Yes
13.3.7.
Answer.
\([B; \land, \lor, -]\) is isomorphic to \([B';\land, \lor, \tilde{}]\) if and only if there exists a function \(T:B \to B'\) such that
-
\(T\) is a bijection;
-
\(\displaystyle T(a\land b)=T(a)\land T(b)\quad \textrm{ for} \textrm{ all } a,b\in B\)
-
\(\displaystyle T(a\lor b)=T(a)\lor T(b)\quad \textrm{ for} \textrm{ all } a, b \in B\)
-
\(T(\bar{a})=\tilde{T(a)}\quad \textrm{ for all } a\in B\text{.}\)
13.4 Atoms of a Boolean Algebra
Exercises
13.4.1.
Answer.
-
For \(a = 3\) we must show that for each \(x \in D_{30}\) one of the following is true: \(x\land 3=3\) or \(x\land 3=1\text{.}\) We do this through the following table:\begin{equation*} \begin{array}{cc} x & \textrm{ verification} \\ \hline \begin{array}{c} 1 \\ 2 \\ 3 \\ 5 \\ 6 \\ 10 \\ 15 \\ 30 \\ \end{array} & \begin{array}{c} 1\land 3=1 \\ 2\land 3=1 \\ 3\land 3=3 \\ 5\land 3=1 \\ 6\land 3=3 \\ 20\land 3=1 \\ 15\land 3=3 \\ 30\land 3=3 \\ \end{array} \\ \end{array} \end{equation*}For \(a=5\text{,}\) a similar verification can be performed.
-
\(6 = 2 \lor 3\text{,}\) \(10 = 2 \lor 5\text{,}\) \(15 = 3 \lor 5\text{,}\) and \(30 = 2 \lor 3 \lor 5\text{.}\)
13.4.3.
Answer.
If \(B = D_{30}\textrm{ }\) 30 then \(A = \{2, 3, 5\}\) and \(D_{30}\) is isomorphic to \(\mathcal{P}(A)\text{,}\) where \(\begin{array}{cc}
1\leftrightarrow \emptyset \textrm{ } & 5\leftrightarrow \{5\} \\
2\leftrightarrow \{2\}\textrm{ } & 10\leftrightarrow \{2,5\} \\
3\leftrightarrow \{3\}\textrm{ } & 15\leftrightarrow \{3,5\} \\
6\leftrightarrow \{2,3\}\textrm{ } & 30\leftrightarrow \{2,3,5\} \\
\end{array}\) and \(\begin{array}{c}
\textrm{ Join} \leftrightarrow \textrm{ Union} \\
\textrm{ Meet}\leftrightarrow \textrm{ Intersection} \\
\textrm{ Complement}\leftrightarrow \textrm{ Set} \textrm{ Complement} \\
\end{array}\)
13.4.5.
Hint.
Answer.
Assume that \(x \neq 0 \textrm{ or } 1\) is the third element of a Boolean algebra. Then there is only one possible set of tables for join and meet, all following from required properties of the Boolean algebra.
\begin{equation*}
\begin{array}{lr}
\begin{array}{c|c}
\lor &
\begin{array}{ccc}
0 & x & 1 \\
\end{array}
\\
\hline
\begin{array}{c}
0 \\
x \\
1 \\
\end{array}
&
\begin{array}{ccc}
0 & x & 1 \\
x & x & 1 \\
1 & 1 & 1 \\
\end{array}
\\
\end{array}
&
\begin{array}{c|c}
\land &
\begin{array}{ccc}
0 & x & 1 \\
\end{array}
\\
\hline
\begin{array}{c}
0 \\
x \\
1 \\
\end{array}
&
\begin{array}{ccc}
0 & 0 & 0 \\
0 & x & x \\
0 & x & 1 \\
\end{array}
\\
\end{array}
\end{array}
\end{equation*}
Next, to find the complement of \(x\) we want \(y\) such that \(x \land y = 0\) and \(x \lor y = 1\text{.}\) No element satisfies both conditions; hence the lattice is not complemented and cannot be a Boolean algebra. The lack of a complement can also be seen from the ordering diagram from which \(\land\) and \(\lor\) must be derived.
13.4.7.
Answer.
Let \(X\) be any countably infinite set, such as the integers. A subset of \(X\) is cofinite if it is finite or its complement is finite. The set of all cofinite subsets of \(X\) is:
-
Countably infinite - this might not be obvious, but here is a hint. Assume \(X=\left\{x_0,x_1,x_2,\ldots \right\}\text{.}\) For each finite subset \(A\) of \(X\text{,}\) map that set to the integer \(\sum _{i=0}^{\infty } \chi _A \left(x_i\right)2^i\) You can do a similar thing to sets that have a finite complement, but map them to negative integers. Only one minor adjustment needs to be made to accommodate both the empty set and \(X\text{.}\)
-
Closed under union
-
Closed under intersection, and
-
Closed under complementation.
Therefore, if \(B =\{A \subseteq X : A \textrm{ is cofinite}\}\text{,}\) then \(B\) is a countable Boolean algebra under the usual set operations.
13.4.8.
13.5 Finite Boolean Algebras as \(n\)-tuples of 0’s and 1’s
Exercises
13.5.1.
Answer.
-
\begin{equation*} \begin{array}{lc} \begin{array}{c|cccc} \lor & (0,0) & (0,1) & (1,0) & (1,1) \\ \hline (0,0) & (0,0) & (0,1) & (1,0) & (1,1) \\ (0,1) &(0,1) & (0,1) & (1,1) & (1,1) \\ (1,0) & (1,0) & (1,1) & (1,0) & (1,1) \\ (1,1) & (1,1) & (1,1) & (1,1) & (1,1) \\ \end{array} &\\ \begin{array}{c|cccc} \land & (0,0) & (0,1) & (1,0) & (1,1) \\ \hline (0,0) &(0,0) & (0,0) & (0,0) & (0,0) \\ (0,1) &(0,0) & (0,1) & (0,0) & (0,1) \\ (1,0) &(0,0) & (0,0) & (1,0) & (1,0) \\ (1,1) &(0,0) & (0,1) & (1,0) & (1,1) \\ \end{array} & \begin{array}{c|c} u & \overset{\pmb{\_}}{u} \\ \hline (0,0) & (1,1) \\ (0,1) &(1,0) \\ (1,0) &(0,1) \\ (1,1) &(0,0) \\ \end{array} \\ \end{array} \end{equation*}
-
The graphs are isomorphic.
-
(0, 1) and (1,0)
13.5.3.
13.6 Boolean Expressions
Exercises
13.6.1.
Answer.
-
\(\displaystyle \begin{array}{l} f_1\left(x_1,x_2\right)=0 \\ f_2\left(x_1,x_2\right)=\left(\overline{x_1}\land \overline{x_2}\right) \\ f_3\left(x_1,x_2\right)=\left(\overline{x_1}\land x_2\right) \\ f_4\left(x_1,x_2\right)=\left(x_1\land \overline{x_2}\right) \\ f_5\left(x_1,x_2\right)=\left(x_1\land x_2\right) \\ f_6\left(x_1,x_2\right)=\left(\left(\overline{x_1}\land \overline{x_2}\right)\lor \left(\overline{x_1}\land x_2\right)\right)=\overline{x_1} \\ f_7\left(x_1,x_2\right)=\left(\left(\overline{x_1}\land \overline{x_2}\right)\lor \left(x_1\land \overline{x_2}\right)\right)=\overline{x_2} \\ f_8\left(x_1,x_2\right)=\left(\left(\overline{x_1}\land \overline{x_2}\right)\lor \left(x_1\land x_2\right)\right)=\left(\left(x_1\land x_2\right)\lor \left(\overline{x_1}\land \overline{x_2}\right)\right) \\ f_9\left(x_1,x_2\right)=\left(\left(\overline{x_1}\land x_2\right)\lor \left(x_1\land \overline{x_2}\right)\right)=\left(\left(x_1\land \overline{x_2}\right)\lor \left(\overline{x_1}\land x_2\right)\right) \\ f_{10}\left(x_1,x_2\right)=\left(\left(\overline{x_1}\land x_2\right)\lor \left(x_1\land x_2\right)\right)=x_2 \\ f_{11}\left(x_1,x_2\right)=\left(\left(x_1\land \overline{x_2}\right)\lor \left(x_1\land x_2\right)\right)=x_1 \\ f_{12}\left(x_1,x_2\right)=\left(\left(\overline{x_1}\land \overline{x_2}\right)\lor \left(\overline{x_1}\land x_2\right)\lor \left(x_1\land \overline{x_2}\right)\right)=\left(\overline{x_1}\lor \overline{x_2}\right) \\ f_{13}\left(x_1,x_2\right)=\left(\left(\overline{x_1}\land \overline{x_2}\right)\lor \left(\overline{x_1}\land x_2\right)\lor \left(x_1\land x_2\right)\right)=\left(\overline{x_1}\lor x_2\right) \\ f_{14}\left(x_1,x_2\right)=\left(\left(\overline{x_1}\land \overline{x_2}\right)\lor \left(x_1\land \overline{x_2}\right)\lor \left(x_1\land x_2\right)\right)=\left(x_1\lor \overline{x_2}\right) \\ f_{15}\left(x_1,x_2\right)=\left(\left(\overline{x_1}\land x_2\right)\lor \left(x_1\land \overline{x_2}\right)\lor \left(x_1\land x_2\right)\right)=\left(x_1\lor x_2\right) \\ f_{16}\left(x_1,x_2\right)=\left(\left(\overline{x_1}\land \overline{x_2}\right)\lor \left(\overline{x_1}\land x_2\right)\lor \left(x_1\land \overline{x_2}\right)\lor \left(x_1\land x_2\right)\right)=1 \\ \end{array}\)
-
The truth table for the functions in part (a) are\begin{equation*} \begin{array}{llllllllll} x_1 & x_2 & f_1 & f_2 & f_3 & f_4 & f_5 & f_6 & f_7 & f_8\\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 1 & 1 & 1 \\ 0 & 1 & 0 & 0 & 1 & 0 & 0 & 1 & 0 & 0\\ 1 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 1 & 0 \\ 1 & 1 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 1 \\ \end{array} \end{equation*}\begin{equation*} \begin{array}{llllllllll} x_1 & x_2 & f_9 & f_{10} & f_{11} & f_{12} & f_{13} & f_{14} & f_{15} & f_{16} \\ 0 & 0 & 0 & 0 & 0 & 1 & 1 & 1 & 0 & 1 \\ 0 & 1 & 1 & 1 & 0 & 1 & 1 & 0 & 1 & 1 \\ 1 & 0 & 1 & 0 & 1 & 1 & 0 & 1 & 1 & 1 \\ 1 & 1 & 0 & 1 & 1 & 0 & 1 & 1 & 1 & 1 \\ \end{array} \end{equation*}
-
-
\(\displaystyle g_1\left(x_1,x_2\right)=f_{15}\left(x_1,x_2\right)\)
-
\(\displaystyle g_2\left(x_1,x_2\right)=f_{12}\left(x_1,x_2\right)\)
-
\(\displaystyle g_3\left(x_1,x_2\right)=f_{12}\left(x_1,x_2\right)\)
-
\(\displaystyle g_4\left(x_1,x_2\right)=f_{16}\left(x_1,x_2\right)\)
-
13.6.3.
Answer.
-
With two variables, there are \(4^3 = 256\) different Boolean functions. With three variables, there are \(4^8=65536\) different Boolean functions.
-
\(\displaystyle f\left(x_1,x_2\right)=\left(1\land \overline{x_1}\land \overline{x_2}\right)\lor \left(1\land \overline{x_1}\land x_2\right)\lor \left(1\land x_1\land \overline{x_2}\right)\lor \left(0\land x_1\land x_2\right)\)
-
Consider \(f:B^2\to B\text{,}\) defined by \(f(0,0)=0\text{,}\) \(f(0,1)=1\text{,}\) \(f(1,0)=a\text{,}\) \(f(1,1)=a\text{,}\) and \(f(0,a)=b\text{,}\) with the images of all other pairs in \(B^2\) defined arbitrarily. This function is not a Boolean function. If we assume that it is Boolean function then \(f\) can be computed with a Boolean expression \(M\left(x_1,x_2\right)\text{.}\) This expression can be put into minterm normal form: \(M\left(x_1,x_2\right)=\left(c_1\land \overline{x_1}\land \overline{x_2}\right)\lor \left(c_2\land \overline{x_1}\land x_2\right)\lor \left(c_3\land x_1\land \overline{x_2}\right)\lor \left(c_4\land x_1\land x_2\right)\)\begin{equation*} \begin{array}{c} f(0,0)=0 \Rightarrow M(0,0)=0 \Rightarrow c_1= 0\\ f(0,1)=1 \Rightarrow M(0,0)=1 \Rightarrow c_2= 1\\ f(1,0)=a \Rightarrow M(0,0)=a \Rightarrow c_3= a\\ f(1,1)=a \Rightarrow M(0,0)=a \Rightarrow c_4= a\\ \end{array} \end{equation*}Therefore, \(M\left(x_1,x_2\right)=\left(\overline{x_1}\land x_2\right)\lor \left(a\land x_1\land \overline{x_2}\right)\lor \left(a\land x_1\land x_2\right)\) and so, using this formula, \(M(0,a)=\left(\bar{0}\land a\right)\lor \left(a\land 0\land \bar{a}\right)\lor (a\land 0\land a)=a\) This contradicts \(f(0,a)=b\text{,}\) and so \(f\) is not a Boolean function.
13.7 A Brief Introduction to Switching Theory and Logic Design
Exercises
13.7.1.
13.7.2.
13.7.3.
14 Monoids and Automata
14.1 Monoids
Exercises
14.1.1.
Answer.
-
\(S_1\) is not a submonoid since the identity of \(\left[\mathbb{Z}_8; \times_8\right]\text{,}\) which is 1, is not in \(S_1\text{.}\) \(S_2\) is a submonoid since \(1 \in S_2\) and \(S_2\) is closed under multiplication; that is, for all \(a, b \in S_2\text{,}\) \(a \times_8 b\) is in \(S_2\text{.}\)
-
The identity of \(\mathbb{N}^{\mathbb{N}}\) is the identity function \(i:\mathbb{N}\to \mathbb{N}\) defined by \(i(a) = a\text{,}\) \(\forall a\in \mathbb{N}\text{.}\) If \(a \in \mathbb{N}\text{,}\) \(i(a) = a \leq a\text{,}\) thus the identity of \(\mathbb{N}^{\mathbb{N}}\) is in \(S_1\text{.}\) However, the image of 1 under any function in \(S_2\) is 2, and thus the identity of \(\mathbb{N}^{\mathbb{N}}\) is not in \(S_2\text{,}\) so \(S_2\) is not a submonoid. The composition of any two functions in \(S_1\text{,}\) \(f\) and \(g\text{,}\) will be a function in \(S_1\text{:}\)\begin{equation*} \begin{split} (f\circ g)(n) & = f(g(n)) \leq g(n)\textrm{ since } f \textrm{ is in } S_1\\ & \leq n\textrm{ since } g \textrm{ is in } S_1 \Rightarrow f \circ g \in S_1 \end{split} \end{equation*}and the two conditions of a submonoid are satisfied and \(S_1\) is a submonoid of \(\mathbb{N}^{\mathbb{N}}\text{.}\)
-
The first set is a submonoid, but the second is not since the null set has a non-finite complement.
14.1.3.
Answer.
The set of \(n \times n\) real matrices is a monoid under matrix multiplication. This follows from the laws of matrix algebra in Chapter 5. To prove that the set of stochastic matrices is a monoid over matrix multiplication, we need only show that the identity matrix is stochastic (this is obvious) and that the set of stochastic matrices is closed under matrix multiplication. Let \(A\) and \(B\) be \(n \times n\) stochastic matrices.
\begin{equation*}
(AB)_{i j}= \sum _{k=1}^n a_{i k} b_{k j}
\end{equation*}
The sum of the \(j^{\textrm{th}}\) column is
\begin{equation*}
\begin{split}
\sum_{j=1}^n (AB)_{i j} & =\sum_{k=1}^n a_{1 k} b_{k j}+\sum_{k=1}^n a_{1k} b_{k j}+\cdots +\sum_{k=1}^n a_{n k} b_{k j}\\
&=\sum_{k=1}^n \left(a_{1 k} b_{k j}+a_{1k} b_{k j}+\cdots +a_{n k} b_{k j}\right)\\
&=\sum _{k=1}^n b_{k j}\left(a_{1 k} +a_{1k}+\cdots +a_{n k} \right)\\
&= \sum _{k=1}^n b_{k j} \quad\textrm{ since } A \textrm{ is stochastic}\\
& = 1 \quad\textrm{ since } B \textrm{ is stochastic}\\
\end{split}
\end{equation*}
14.1.5.
Answer.
Let \(f, g, h \in M\text{,}\) and \(a \in B\text{.}\)
\begin{equation*}
\begin{split}
((f*g)*h)(a) & = (f*g)(a) \land h(a)\\
& = (f(a)\land g(a))\land h(a)\\
& = f(a) \land ( g(a) \land h(a))\\
& = f(a) \land (g * h)(a)\\
& = (f * (g * h))(a)\\
\end{split}
\end{equation*}
Therefore \((f * g) * h =f * (g * h)\) and \(*\) is associative.
The identity for \(*\) is the function \(u \in M\) where \(u(a) = 1\) = the “one” of \(B\text{.}\) If \(a \in B\text{,}\) \((f*u)(a) =f(a)\land u(a) = f(a)\land 1 = f(a)\text{.}\) Therefore \(f * u = f\text{.}\) Similarly, \(u * f =f\text{.}\)
There are \(2^2= 4\) functions in \(M\) for \(B = B _2\text{.}\) These four functions are named in the text. See Figure 14.1.4. The table for \(*\) is
\begin{equation*}
\begin{array}{c|cccc}
* & z & i & t & u\\
\hline
z &z & z & z & z \\
i &z & i & z & i \\
t &z & z & t & t \\
u &z & i & t & u \\
\end{array}
\end{equation*}
14.2 Free Monoids and Languages
Exercises
14.2.1.
14.2.3.
14.2.5.
Answer.
-
Terminal symbols: The null string, 0, and 1. Nonterminal symbols: \(S\text{,}\) \(E\text{.}\) Starting symbol: \(S\text{.}\) Production rules: \(S\to 00S\text{,}\) \(S\to 01S\text{,}\) \(S\to 10S\text{,}\) \(S\to 11S\text{,}\) \(S\to E\text{,}\) \(E\to 0\text{,}\) \(E\to 1\) This is a regular grammar.
-
Terminal symbols: The null string, 0, and 1. Nonterminal symbols: \(S\text{,}\) \(A\text{,}\) \(B\text{,}\) \(C\) Starting symbol: \(S\) Production rules: \(S \to 0A\text{,}\) \(S \to 1A\text{,}\) \(S \to \lambda\) , \(A \to 0B\text{,}\) \(A \to 1B\text{,}\) \(A \to \lambda\text{,}\) \(B \to 0C\text{,}\) \(B \to 1C\text{,}\) \(B \to A\text{,}\) \(C \to 0\text{,}\) \(C \to 1\text{,}\) \(C \to \lambda\) This is a regular grammar.
-
See Exercise 3. This language is not regular.
14.2.7.
14.2.9.
Answer.
-
List the elements of each set \(X_i\) in a sequence \(x_{i 1}\text{,}\) \(x_{i 2}\text{,}\) \(x_{i 3}\ldots\) . Then draw arrows as shown below and list the elements of the union in order established by this pattern: \(x_{11}\text{,}\) \(x_{21}\text{,}\) \(x_{12}\text{,}\) \(x_{13}\text{,}\) \(x_{22}\text{,}\) \(x_{31}\text{,}\) \(x_{41}\text{,}\) \(x_{32}\text{,}\) \(x_{23}\text{,}\) \(x_{14}\text{,}\) \(x_{15}\ldots \text{,}\)
-
Each of the sets \(A^1\) , \(A^2\) , \(A^3, \ldots\text{,}\) are countable and \(A^*\) is the union of these sets; hence \(A^*\) is countable.
Exercise 9
14.3 Automata, Finite-State Machines
Exercises
14.3.1.
Answer.
\begin{equation*}
\begin{array}{cccc}
x & s & Z(x,s) & t(x,s) \\
\textrm{ Deposit} 25\not{c} & \textrm{ Locked} & \textrm{ Nothing} & \textrm{ Select} \\
\textrm{ Deposit} 25\not{c} & \textrm{ Select} & \textrm{ Return} 25\not{c} & \textrm{ Select} \\
\textrm{ Press} S & \textrm{ Locked} & \textrm{ Nothing} & \textrm{ Locked} \\
\textrm{ Press} S & \textrm{ Select} & \textrm{ Dispense} S & \textrm{ Locked} \\
\textrm{ Press} P & \textrm{ Locked} & \textrm{ Nothing} & \textrm{ Locked} \\
\textrm{ Press} P & \textrm{ Select} & \textrm{ Dispense} P & \textrm{ Locked} \\
\textrm{ Press} B & \textrm{ Locked} & \textrm{ Nothing} & \textrm{ Locked} \\
\textrm{ Press} B & \textrm{ Select} & \textrm{ Dispense} B & \textrm{ Locked} \\
\end{array}
\end{equation*}
Vending Machine Transitions
14.3.3.
14.3.5.
Answer.
-
-
Input: 10110, Output: 11011 \(\Rightarrow\) 10110 is in position 27
-
Input: 00100, Output: 00111 \(\Rightarrow\) 00100 is in position 7
-
Input:11111, Output: 10101 \(\Rightarrow\) 11111 is in position 21
-
-
Let \(x=x_1x_2\ldots x_n\) and recall that for \(n\geq 1\text{,}\) \(G_{n+1}=\left( \begin{array}{c} 0G_n \\ 1G_n^r \\ \end{array} \right)\text{,}\) where \(G_n^r\) is the reverse of \(G_n\text{.}\) To prove that the Gray Code Decoder always works, let \(p(n)\) be the proposition “Starting in Copy state, \(x\)’s output is the position of \(x\) in \(G_n\text{;}\) and starting in Complement state, \(x\)’s output is the position of \(x\) in \(G_n^r\text{.}\)” That p(1) is true is easy to verify for both possible values of \(x\text{,}\) 0 and 1. Now assume that for some \(n\geq 1\text{,}\) \(p(n)\) is true and consider \(x=x_1x_2\ldots x_nx_{n+1}\text{.}\)If \(x_1=0\text{,}\) \(x\)’s output is a zero followed by the output for \(\left(x_2\ldots x_nx_{n+1}\right)\) starting in Copy state. By the induction hypothesis, this is zero followed by the position of \(\left(x_2 \ldots x_n x_{n+1}\right)\) in \(G_n\text{,}\) which is the position of \(x\) in \(G_{n+1}\text{,}\) by the definition of \(G\text{.}\)If \(x_1=1\text{,}\) \(x\)’s output is a one followed by the output for \(\left(x_2\ldots x_nx_{n+1}\right)\) starting in Complement state. By the induction hypothesis, this is one followed by the position of \(\left(x_2\ldots x_nx_{n+1}\right)\) in \(G_n^r\text{,}\) which is the position of \(x\) in \(G_{n+1}\text{,}\) by the definition of \(G\text{.}\) \(\square\)
14.4 The Monoid of a Finite-State Machine
Exercises
14.4.1.
Answer.
-
\(\begin{array}{c|cccccc} \textrm{ Input String} & a & b & c & aa & ab & ac \\ \hline 1 & (a,1) & (a,2) & (c,3) & (a,1) & (a,2) & (c,3) \\ 2 & (a,2) & (a,1) & (c,3) & (a,2) & (a,1) & (c,3) \\ 3 & (c,3) & (c,3) & (c,3) & (c,3) & (c,3) & (c,3) \\ \end{array}\) \(\begin{array}{c|cccccc} \textrm{ Input String} & ba & bb & bc & ca & cb & cc \\ \hline 1 & (a,2) & (a,1) & (c,3) & (c,3) & (c,3) & (c,3) \\ 2 & (a,1) & (a,2) & (c,3) & (c,3) & (c,3) & (c,3) \\ 3 & (c,3) & (c,3) & (c,3) & (c,3) & (c,3) & (c,3) \\ \end{array}\)We can see that \(T_aT_a= T_{\textrm{ \textit{aa}}}=T_a\text{,}\) \(T_aT_b= T_{\textrm{ \textit{ab}}}= T_b\text{,}\) etc. Therefore, we have the following monoid:\begin{equation*} \begin{array}{c|c} & \begin{array}{ccc} T_{a} & T_b & T_b \\ \end{array} \\ \hline \begin{array}{c} T_a \\ T_b \\ T_c \\ \end{array} & \begin{array}{ccc} T_a & T_b & T_c \\ T_b & T_a & T_c \\ T_c & T_c & T_c \\ \end{array} \\ \end{array} \end{equation*}Notice that \(T_a\) is the identity of this monoid.
-
\(\begin{array}{c|cccccc} \textrm{Input String} & 1 & 2 & 11 & 12 & 21 & 22 \\ \hline A & C & B & A & D & D & A \\ B & D & A & B & C & C & B \\ C & A & D & C & B & B & C \\ D & B & C & D & A & A & D \\ \end{array}\)\(\begin{array}{c|cccccccc} \textrm{Input String} &111 & 112 & 121 & 122 & 211 & 212 & 221 & 222 \\ \hline A & C & B & B & C & B & C & C & B \\ B & D & A & A & D & A & D & D & A \\ C & B & C & C & B & C & B & B & C \\ D & B & C & C & B & C & B & B & C \\ \end{array}\)We have the following monoid:\begin{equation*} \begin{array}{c|c} & \begin{array}{cccc} T_1 & T_2 & T_{11} & T_{12} \\ \end{array} \\ \hline \begin{array}{c} T_1 \\ T_2 \\ T_{11} \\ T_{12} \\ \end{array} & \begin{array}{cccc} T_{11} & T_{12} & T_1 & T_2 \\ T_b & T_{11} & T_2 & T_1 \\ T_1 & T_2 & T_{11} & T_{12} \\ T_2 & T_1 & T_{12} & T_{11} \\ \end{array} \\ \end{array} \end{equation*}Notice that \(T_{11}\) is the identity of this monoid.
14.4.3.
Answer.
Yes, just consider the unit time delay machine of Figure 14.4.4. Its monoid is described by the table at the end of Section 14.4 where the \(T_{\lambda
}\) row and \(T_{\lambda }\) column are omitted. Next consider the machine in Figure 14.5.7. The monoid of this machine is:
\begin{equation*}
\begin{array}{c|ccccccc}
& T_{\lambda } & T_0 & T_1 & T_{00} & T_{01} & T_{10} & T_{11} \\
\hline
T_{\lambda } & T_{\lambda } & T_0 & T_1 & T_{00} & T_{01} & T_{10} & T_{11} \\
\hline
T_0 & T_0 & T_{00} & T_{01} & T_{00} & T_{01} & T_{10} & T_{11} \\
T_1 & T_1 & T_{10} & T_{11} & T_{00} & T_{01} & T_{10} & T_{11} \\
T_{00} & T_{00} & T_{00} & T_{01} & T_{00} & T_{01} & T_{10} & T_{11} \\
T_{01} & T_{01} & T_{10} & T_{11} & T_{00} & T_{01} & T_{10} & T_{11} \\
T_{10} & T_{10} & T_{00} & T_{01} & T_{00} & T_{01} & T_{10} & T_{11} \\
T_{11} & T_{11} & T_{10} & T_{11} & T_{00} & T_{01} & T_{10} & T_{11} \\
\end{array}
\end{equation*}
Hence both of these machines have the same monoid, however, their transition diagrams are nonisomorphic since the first has two vertices and the second has seven.
14.5 The Machine of a Monoid
Exercises
14.5.1.
15 Group Theory and Applications
15.1 Cyclic Groups
Exercises
15.1.1.
15.1.3.
Answer.
If \(\lvert G \rvert = m\text{,}\) \(m>2\text{,}\) and \(G = \langle a \rangle\text{,}\) then \(a\text{,}\) \(a^2,\ldots\text{,}\) \(a^{m-1}\) , \(a^m=e\) are distinct elements of \(G\text{.}\) Furthermore, \(a^{-1}= a^{m-1}\neq a\text{,}\) If \(1 \leq k \leq m\text{,}\) \(a^{-1}\) generates \(a^k\text{:}\)
\begin{equation*}
\begin{split}
\left(a^{-1}\right)^{m-k} &= \left(a^{m-1}\right)^{m-k}\\
& = a^{m^2-m-m k + k}\\
& =\left(a^m\right)^{m-k-1}*a^k\\
&= e*a^k=a^k\\
\end{split}
\end{equation*}
Similarly, if \(G\) is infinite and \(G = \langle a\rangle\text{,}\) then \(a^{-1}\) generates \(G\text{.}\)
15.1.5.
Answer.
-
No. Assume that \(q \in \mathbb{Q}\) generates \(\mathbb{Q}\text{.}\) Then \(\langle q\rangle = \{n q : n \in \mathbb{Z}\}\text{.}\) But this gives us at most integer multiples of \(q\text{,}\) not every element in \(\mathbb{Q}\text{.}\)
-
No. Similar reasoning to part a.
-
Yes. 6 is a generator of \(6\mathbb{Z}\text{.}\)
-
No.
-
Yes, \((1,1, 1)\) is a generator of the group.
15.1.7.
Answer.
Theorem 15.1.13 implies that \(a\) generates \(\mathbb{Z}_n\) if and only if the greatest common divisor of \(n\) and \(a\) is 1. Therefore the list of generators of \(\mathbb{Z}_n\) are the integers in \(\mathbb{Z}_n\) that are relatively prime to \(n\text{.}\) The generators of \(\mathbb{Z}_{25}\) are all of the nonzero elements except 5, 10, 15, and 20. The generators of \(\mathbb{Z}_{256}\) are the odd integers in \(\mathbb{Z}_{256}\) since 256 is \(2^8\text{.}\)
15.1.9.
Answer.
-
\(\theta :\mathbb{Z}_{77} \to \mathbb{Z}_7 \times \mathbb{Z}_{11}\) maps the given integers as follows:\begin{equation*} \begin{array}{ccc} 21 & \to & (0,10) \\ 5 & \to & (5,5) \\ 7 & \to & (0,7) \\ 15 & \to & \underline{(1,4)} \\ \textrm{ sum}=48 & \leftarrow & (6,4)=\textrm{ sum} \\ \end{array} \end{equation*}The final sum, 48, is obtained by using the facts that \(\theta ^{-1}(1,0) =22\) and \(\theta ^{-1}(0,1)=56\)\begin{equation*} \begin{split} \theta^{-1}(6,4)= 6 \times_{77}\theta ^{-1}(1,0) + 4 \times_{77}\theta^{-1}(0,1)\\ & =6\times_{77}22 +_{77} 4\times_{77} 56\\ & =55 +_{77}70\\ & =48\\ \end{split}\text{.} \end{equation*}
-
Using the same isomorphism:\begin{equation*} \begin{array}{ccc} 25 & \to & (4,3) \\ 26 & \to & (5,4) \\ 40 & \to & (5,7) \\ & & \textrm{ sum}=(0,3) \\ \end{array} \end{equation*}\begin{equation*} \begin{split} theta ^{-1}(0,3) &= 3 \times_{77}\theta ^{-1}(0,1)\\ & = 3\times_{77} 56\\ & =14\\ \end{split}\text{.} \end{equation*}The actual sum is 91. Our result is incorrect, since 91 is not in \(\mathbb{Z}_{77}\text{.}\) Notice that 91 and 14 differ by 77. Any error that we get using this technique will be a multiple of 77.
15.2 Cosets and Factor Groups
Exercises
15.2.1.
Answer.
An example of a valid correct answer: Call the subsets \(A\) and \(B\) respectively. If we choose \(0 \in A\) and \(5 \in B\) we get \(0 +_{10} 5 =5 \in B\text{.}\) On the other hand, if we choose \(3 \in A\) and \(8 \in B\text{,}\) we get \(3 +_{10} 8 = 1 \in A\text{.}\) Therefore, the induced operation is not well defined on \(\{A,B\}\text{.}\)
15.2.3.
Answer.
-
The four distinct cosets in \(G/H\) are \(H = \{(0, 0), (2, 0)\}\text{,}\) \((1, 0) + H= \{(1,0),(3,0)\}\text{,}\) \((0, 1) + H= \{(0,1),(2,1)\}\text{,}\) and \((1, 1) + H= \{(1,1),(3,1)\}\text{.}\) None of these cosets generates \(G/H\text{;}\) therefore \(G/H\) is not cyclic. Hence \(G/H\) must be isomorphic to \(\mathbb{Z}_2\times \mathbb{Z}_2\text{.}\)
-
The factor group is isomorphic to \([\mathbb{R}; +]\text{.}\) Each coset of \(\mathbb{R}\) is a line in the complex plane that is parallel to the x-axis: \(\tau :\mathbb{C}/\mathbb{R}\to \mathbb{R}\text{,}\) where \(T(\{a + b i\mid a\in \mathbb{R}\}) = b\) is an isomorphism.
-
\(\langle 8\rangle = \{0, 4, 8, 12, 16\} \)\(\Rightarrow\) \(\lvert \mathbb{Z}_{20}/\langle 8\rangle \rvert =4\text{.}\) The four cosets are: \(\bar{0}\text{,}\) \(\bar{1}\text{,}\) \(\bar{2}\text{,}\) and \(\bar{3}\text{.}\) 1 generates all four cosets. The factor group is isomorphic to \([\mathbb{Z}_4; +_4]\) because \(\bar{1}\) is a generator.
15.2.5.
15.3 Permutation Groups
15.3.5 Exercises
15.3.5.1.
Answer.
-
\(\displaystyle \left( \begin{array}{cccc} 1 & 2 & 3 & 4 \\ 1 & 4 & 3 & 2 \\ \end{array} \right)\)
-
\(\displaystyle \left( \begin{array}{cccc} 1 & 2 & 3 & 4 \\ 4 & 3 & 1 & 2 \\ \end{array} \right)\)
-
\(\displaystyle \left( \begin{array}{cccc} 1 & 2 & 3 & 4 \\ 3 & 4 & 2 & 1 \\ \end{array} \right)\)
-
\(\displaystyle \left( \begin{array}{cccc} 1 & 2 & 3 & 4 \\ 3 & 4 & 2 & 1 \\ \end{array} \right)\)
-
\(\displaystyle \left( \begin{array}{cccc} 1 & 2 & 3 & 4 \\ 4 & 2 & 1 & 3 \\ \end{array} \right)\)
-
\(\displaystyle \left( \begin{array}{cccc} 1 & 2 & 3 & 4 \\ 3 & 1 & 4 & 2 \\ \end{array} \right)\)
-
\(\displaystyle \left( \begin{array}{cccc} 1 & 2 & 3 & 4 \\ 2 & 1 & 4 & 3 \\ \end{array} \right)\)
15.3.5.3.
15.3.5.5.
Answer.
\(\mathcal{D}_4 = \left\{i, r, r^2, r^3, f_1, f_2, f_3, f_4\right\}\) Where \(i\) is the identity function, \(r=\left(
\begin{array}{cccc}
1 & 2 & 3 & 4 \\
2 & 3 & 4 & 1 \\
\end{array}
\right)\text{,}\) and
\begin{equation*}
\begin{array}{cc}
f_1 =\left(
\begin{array}{cccc}
1 & 2 & 3 & 4 \\
4 & 3 & 2 & 1 \\
\end{array}
\right) & f_2 =\left(
\begin{array}{cccc}
1 & 2 & 3 & 4 \\
2 & 1 & 4 & 3 \\
\end{array}
\right) \\
f_3 =\left(
\begin{array}{cccc}
1 & 2 & 3 & 4 \\
3 & 2 & 1 & 4 \\
\end{array}
\right) & f_4 =\left(
\begin{array}{cccc}
1 & 2 & 3 & 4 \\
1 & 4 & 3 & 2 \\
\end{array}
\right) \\
\end{array}
\end{equation*}
The operation table for the group is
\begin{equation*}
\begin{array}{c|c}
\circ & \textrm{ }
\begin{array}{cccccccc}
i & r & r^2 & r^3 & f_1 & f_2 & f_3 & f_4 \\
\end{array}
\\
\hline
\begin{array}{c}
i \\
r \\
r^2 \\
r^3 \\
f_1 \\
f_2 \\
f_3 \\
f_4 \\
\end{array}
&
\begin{array}{cccccccc}
i & r & r^2 & r^3 & f_1 & f_2 & f_3 & f_4 \\
r & r^2 & r^3 & i & f_4 & f_3 & f_1 & f_2 \\
r^2 & r^3 & i & r & f_2 & f_1 & f_4 & f_3 \\
r^3 & i & r & r^2 & f_3 & f_4 & f_2 & f_1 \\
f_1 & f_3 & f_2 & f_4 & i & r^2 & r & r^3 \\
f_2 & f_4 & f_1 & f_3 & r^2 & i & r^3 & r \\
f_3 & f_2 & f_4 & f_1 & r^3 & r & i & r^2 \\
f_4 & f_1 & f_3 & f_2 & r & r^3 & r^2 & i \\
\end{array}
\\
\end{array}
\end{equation*}
A lattice diagram of its subgroups is
Subgroups of \(\mathcal{D}_4\)
All proper subgroups are cyclic except \(\left\{i,r^2,f_1,f_2\right\}\)\(\textrm{ }\textrm{ }\)and \(\left\{i,r^2,f_3,f_4\right\}\text{.}\) Each 2-element subgroup is isomorphic to \(\mathbb{Z}_2\) ; \(\left\{i,r,r^2,r^3\right\}\) is isomorphic to \(\mathbb{Z}_4\) ; and \(\left\{i,r^2,f_1,f_2\right\}\)\(\textrm{ }\textrm{ }\)and \(\left\{i,r^2,f_3,f_4\right\}\) are isomorphic to \(\mathbb{Z}_2\times \mathbb{Z}_2\text{.}\)
15.3.5.7.
Answer.
One solution is to cite Exercise 3 at the end of Section 11.3. It can be directly applied to this problem. An induction proof of the problem at hand would be almost identical to the proof of the more general statement. \(\left(t_1t_2\cdots t_r\right){}^{-1}= t_r{}^{-1}\cdots t_2{}^{-1}t_1{}^{-1}\quad\textrm{ by Exercise 3 of Section 11.3}\\
\\
\quad \quad = t_r\cdots t_2t_1\textrm{ }\textrm{ since} \textrm{ each} \textrm{ transposition} \textrm{ inverts} \textrm{ itself}.\textrm{ }\square\)
15.3.5.9.
Answer.
Part I: That \(\lvert S_k \rvert = k!\) follows from the Rule of Products.
Part II: Let \(f\) be the function defined on \(\{1,2,\textrm{ ...}, n\}\) by \(f(1)=2\text{,}\) \(f(2)=3\text{,}\) \(f(3)=1\text{,}\) and \(f(j) =j\) for \(4\leq j\leq n\text{;}\) and let \(g\) be defined by \(g(1) = 1\text{,}\) \(g(2) = 3\text{,}\) \(g(3) = 2\text{,}\) and \(g(j) =j\) for \(4\leq j\leq n\text{.}\) Note that \(f\) and \(g\) are elements of \(S_n\text{.}\) Next, \((f\circ g)(1) = f(g(1)) = f(1) = 2\text{,}\) while \((g \circ f)(1) = g(f(1)) = g(2) =
3\text{,}\) hence \(f\circ g\neq g\circ f\) and \(S_n\) is non-abelian for any \(n \geq 3\text{.}\)
15.3.5.13.
Answer.
-
Both groups are non-abelian and of order 6; so they must be isomorphic, since only one such group exists up to isomorphism. The function \(\theta:S_3\to R_3\) defined by \(\begin{array}{cc} \theta(i)=I & \theta\left(f_1\right)=F_1 \\ \theta\left(r_1\right)=R_1 & \theta\left(f_2\right)=F_2 \\ \theta\left(r_2\right)=R_2 & \theta\left(f_3\right)=F_3 \\ \end{array}\) is an isomorphism,
-
Recall that since every function is a relation, it is natural to translate functions to Boolean matrices. Suppose that \(f\in S_n\text{.}\) We will define its image, \(\theta(f)\text{,}\) by\begin{equation*} \theta(f)_{kj}=1\textrm{ }\Leftrightarrow \textrm{ }f(j)=k \end{equation*}That \(\theta\) is a bijection follows from the existence of \(\theta^{-1}\text{.}\) If \(A\) is a rook matrix,\begin{equation*} \begin{split} \theta^{-1}(A)(j)=k &\Leftrightarrow \textrm{ }\textrm{The } 1 \textrm{ in} \textrm{ column } j \textrm{ of } A \textrm{ appears} \textrm{ in} \textrm{ row } k \\ &\Leftrightarrow A_{kj}=1 \end{split} \end{equation*}For \(f,g\in S_n\text{,}\)\begin{equation*} \begin{split} \theta(f\circ g)_{kj}= 1 & \Leftrightarrow \textrm{ }(f \circ g)(j)=k\\ & \Leftrightarrow \exists l\textrm{ such that }g(j)=l \textrm{ and } f(l)=k\\ & \Leftrightarrow \exists l\textrm{ such that } \theta(g)_{lj}=1\textrm{ and }\textrm{}\theta(f)_{kl}=1\\ & \Leftrightarrow (\theta(f)\theta(g))_{kj}=1 \end{split} \end{equation*}Therefore, \(\theta\) is an isomorphism.
15.4 Normal Subgroups and Group Homomorphisms
15.4.3 Exercises
15.4.3.1.
Answer.
-
Yes, the kernel is \(\{1, -1\}\)
-
No, since \(\theta _2\left(2 +_{5} 4\right)= \theta_2(1)=1\text{,}\) but \(\theta _2(2)+_2\theta_{2} (4)=0+_{2}0 =0\)A follow-up might be to ask what happens if 5 is replaced with some other positive integer in this part.
-
Yes, the kernel is \(\{(a, -a)| a \in \mathbb{R}\}\)
-
No. A counterexample, among many, would be to consider the two transpositions \(t_1=(1,3)\) and \(t_2=(1,2)\text{.}\) Compare \(\theta_4(t_1 \circ t_2)\) and \(\theta_4(t_1) \circ \theta_4(t_2)\text{.}\)
15.4.3.3.
Answer.
\(\langle r\rangle =\left\{i,r,r^2,r^3\right\}\) is a normal subgroup of \(D_4\text{.}\) To see you could use the table given in the solution of Exercise 15.3.5.5 of Section 15.3 and verify that \(a^{-1}h a \in \langle r\rangle\) for all \(a\in D_4\) and \(h\in \langle r\rangle\text{.}\) A more efficient approach is to prove the general theorem that if \(H\) is a subgroup \(G\) with exactly two distinct left cosets, than \(H\) is normal. \(\left\langle f_1\right\rangle\) is not a normal subgroup of \(D_4\text{.}\) \(\left\langle f_1\right\rangle =\left\{i,f_1\right\}\) and if we choose \(a = r\) and \(h=f_1\) then \(a^{-1}h a= r^3f_1r=f_2\notin \left\langle f_1\right\rangle\)
15.4.3.5.
15.4.3.7.
Answer.
Let \(x, y \in G\text{.}\)
\begin{equation*}
\begin{split}
q(x * y) &= (x * y)^2\\
& = x*y*x*y \\
& = x*x*y*y \quad\textrm{ since } G \textrm{ is abelian}\\
& =x^2*y^2 \\
&= q(x)*q(y)
\end{split}
\end{equation*}
Hence, \(q\) is a homomorphism. In order for \(q\) to be an isomorphism, it must be the case that no element other than the identity is its own inverse.
\begin{equation*}
\begin{split}
x \in \textrm{Ker}(q) & \Leftrightarrow q (x) = e \\
& \Leftrightarrow x * x =e \\
& \Leftrightarrow x^{-1}= x\\
\end{split}
\end{equation*}
15.4.3.9.
Answer.
Proof: Recall that the inverse image of \(H'\) under \(\theta\) is \(\theta ^{-1}(H')=\{g\in G | \theta (g)\in H'\}\text{.}\)
Closure: Let \(g_1, g_2\in \theta ^{-1}(H')\text{,}\) then \(\theta \left(g_1\right),\theta \left(g_2\right)\in H'\text{.}\) Since \(H'\) is a subgroup of \(G'\text{,}\)
\begin{equation*}
\theta\left(g_1\right)\diamond \theta\left(g_2\right)=\theta\left(g_1*g_2\right)\in H' \Rightarrow g_1*g_2\in \theta^{-1}(H')
\end{equation*}
Inverse: Let \(a\in \theta ^{-1}(H')\) . Then \(\theta (a)\in H'\) and by Theorem 15.4.14(b), \(\theta (a)^{-1}= \theta \left(a^{-1}\right)\in H'\) and so \(a^{-1}\in \theta ^{-1}(H')\text{.}\)
15.5 Coding Theory, Linear Codes
15.5.4 Exercises
15.5.4.1.
15.5.4.3.
Answer.
-
Syndrome = \((1,0,1)\text{.}\) Corrected coded message is \((1,1,0,0,1,1)\) and original message was \((1, 1, 0)\text{.}\)
-
Syndrome = \((1,1,0)\text{.}\) Corrected coded message is \((0,0,1,0,1,1)\) and original message was \((0, 0, 1)\text{.}\)
-
Syndrome = \((0,0,0)\text{.}\) No error, coded message is \((0,1,1,1,1,0)\) and original message was \((0, 1, 1)\text{.}\)
-
Syndrome = \((1, 1,0)\text{.}\) Corrected coded message is \((1,0,0,1,1,0)\) and original message was \((1, 0, 0)\text{.}\)
-
Syndrome = \((1,1,1)\text{.}\) This syndrome occurs only if two bits have been switched. No reliable correction is possible.
-
Syndrome = \((0,1,0)\text{.}\) Corrected coded message is \((1,0,0,1,1,0)\) and original message was \((1, 0, 0)\text{.}\)
15.5.4.5.
Answer.
-
Blocks of two bits are encoded into code words of length 4.
-
The code words are 0000, 1010, 0111 and 1101.
-
Since the first two code words have a Hamming distance of 2, not all single bit errors can be corrected. For example, if 0000 is transmitted and the first bit is switch, then 1000 is received and we can’t tell for sure whether this came from 0000 or 1010. To see what can be corrected, we note that \(a_1 a_2\) is encoded to \(a_1 a_2 (a_1 +_2 a_2) a_2\) and so if \(b_1 b_2 b_3 b_4\) is recieved and no error has occurred,\begin{gather*} b_1 +_2 b_2 +_2 b_3 =0\\ b_2 +_2 b_4 =0 \end{gather*}We can extract the parity check matrix from this set of equations. It is\begin{equation*} \begin{pmatrix} 1 & 0 \\ 1 & 1 \\ 1 & 0 \\ 0 & 1 \end{pmatrix} \end{equation*}The rows of this matrix correspond with the syndromes for errors in bits 1 through 4, which are all nonzero, so we can detect any single bit error. Notice that the syndromes for bits 1 and 3 are identical. This reflects the fact that errors in these bits can’t be corrected. However, the syndromes for bits 2 and 4 are unique and so we can correct them. Therefore the second bit of the original message can be sent with more confidence than the first.
15.5.4.7.
Solution.
Yes, you can correct all single bit errors because the parity check matrix for the expanded code is
\begin{equation*}
H = \left(\begin{array}{ccc}
1 & 1 & 0\\
1 & 0 & 0\\
1 & 0 & 1\\
0 & 1 & 0\\
0 & 1 & 1\\
0 & 0 & 1\\
\end{array} \right).
\end{equation*}
Since each possible syndrome of single bit errors is unique we can correct any error.
15.5.4.8.
16 An Introduction to Rings and Fields
16.1 Rings, Basic Definitions and Concepts
16.1.6 Exercises
16.1.6.1.
Answer.
All but ring d are commutative. All of the rings have a unity element. The number 1 is the unity for all of the rings except d. The unity for \(M_{2\times 2}(\mathbb{R})\) is the two by two identity matrix. The units are as follows:
-
\(\displaystyle \{1, -1\}\)
-
\(\displaystyle \mathbb{C}^*\)
-
\(\displaystyle \mathbb{Q}^*\)
-
\(\displaystyle \left\{A \left| A_{11}A_{22}-A_{12}A_{21}\neq 0\right.\right\}\)
-
\(\displaystyle \{1\}\)
16.1.6.3.
16.1.6.5.
Answer.
-
We already know that \(3\mathbb{Z}\) is a subgroup of the group \(\mathbb{Z}\text{.}\) We need only show that \(3\mathbb{Z}\) is closed with respect to multiplication. Let \(3m, 3n \in 3\mathbb{Z}\text{.}\) \((3m)(3n) = 3(3m n) \in 3\mathbb{Z}\text{,}\) since \(3 m n \in \mathbb{Z}\text{.}\)
-
The proper subrings are \(\{0, 2, 4, 6\}\) and \(\{0, 4\}\text{;}\) while \(\{0\}\) and \(\mathbb{Z}_8\) are improper subrings.
-
The proper subrings are \(\{00, 01\}\text{,}\) \(\{00, 10\}\text{,}\) and \(\{00,11\}\text{:}\) while \(\{00\}\) and \(\mathbb{Z}_2\times \mathbb{Z}_2\) are improper subrings.
16.1.6.7.
Answer.
-
The left-hand side of the equation factors into the product \((x-2)(x-3)\text{.}\) Since \(\mathbb{Z}\) is an integral domain, \(x = 2\) and \(x =3\) are the only possible solutions.
-
Over \(\mathbb{Z}_{12}\text{,}\) 2, 3, 6, and 11 are solutions. Although the equation factors into \((x-2)(x-3)\text{,}\) this product can be zero without making \(x\) either 2 or 3. For example. If \(x\) = 6 we get \((6-2)\times _{12}(6-3)=4 \times _{12}3 = 0\text{.}\) Notice that 4 and 3 are zero divisors.
16.1.6.9.
Answer.
Let \(R_1\text{,}\) \(R_2\text{,}\) and \(R_3\) be any rings, then
-
\(R_1\) is isomorphic to \(R_2\) \(\Rightarrow\) \(R_2\) is isomorphic to \(R_1\text{,}\) and so “is isomorphic to” is a symmetric relation on rings,
-
\(R_1\) is isomorphic to \(R_2\text{,}\) and \(R_2\) is isomorphic to \(R_3\) implies that \(R_1\) is isomorphic to \(R_3\text{,}\) and so “is isomorphic to” is a transitive relation on rings.
We haven’t proven these properties here, just stated them. The combination of these observations implies that “is isomorphic to” is an equivalence relation on rings.
16.1.6.11.
Answer.
-
Commutativity is clear from examination of a multiplication table for \(\mathbb{Z}_2\times \mathbb{Z}_3\text{.}\) More generally, we could prove a theorem that the direct product of two or more commutative rings is commutative. \((1, 1)\) is the unity of \(\mathbb{Z}_2\times \mathbb{Z}_3\text{.}\)
-
\(\displaystyle \{(m, n) | m = 0 \textrm{ or } n = 0, (m, n) \neq (0, 0)\}\)
-
Another example is \(\mathbb{Z} \times \mathbb{Z}\text{.}\) You never get an integral domain in this situation. By the definition an integral domain \(D\) must contain a “zero” so we always have \((1, 0) \cdot (0, 1) = (0, 0)\) in \(D \times D\text{.}\)
16.1.6.13.
Answer.
-
\(\displaystyle (a + b)(c + d) = (a + b)c + (a + b)d = a c + b c + a d + b d\)
-
\begin{equation*} \begin{split} (a + b)(a + b ) &= a a + b a + a b + b b\quad \textrm{ by part a}\\ & = a a + a b + a b + b b\quad \textrm{ since } R \textrm{ is commutative}\\ & =a^2 + 2a b + b^2 \end{split}\text{.} \end{equation*}
16.2 Fields
Exercises
16.2.5.
16.2.7.
16.3 Polynomial Rings
Exercises
16.3.1.
16.3.3.
16.3.5.
Answer.
-
Reducible, \((x+1)\left(x^2+ x+1\right)\)
-
Reducible, \(x\left(x^2+x+1\right)\)
-
Irreducible. If you could factor this polynomial, one factor would be either \(x\) or \(x + 1\text{,}\) which would give you a root of 0 or 1, respectively. By substitution of 0 and 1 into this polynomial, it clearly has no roots.
-
Reducible, \((x+1)^{4 }\)
16.3.7.
Answer.
We illustrate this property of polynomials by showing that it is not true for a nonprime polynomial in \(\mathbb{Z}_2[x]\text{.}\) Suppose that \(p(x)
= x^2+ 1\text{,}\) which can be reduced to \((x+1)^2\) , \(a(x) = x^2 + x\text{,}\) and \(b(x) = x^3 + x^2\text{.}\) Since \(a(x)b(x) =x^5+x^3= x^3\left(x^2+1\right)\text{,}\) \(p(x)|a(x)b(x)\text{.}\) However, \(p(x)\) is not a factor of either \(a(x)\) or \(b(x)\text{.}\)
16.3.9.
16.3.11.
Answer.
For \(n \geq 0\text{,}\) let \(S(n)\) be the proposition: For all \(g(x)\neq 0\) and \(f(x)\) with \(\deg f(x) = n\text{,}\) there exist unique polynomials \(q(x)\) and \(r(x)\) such that \(f(x)=g(x)q(x)+r(x)\text{,}\) and either \(r(x)=0\) or \(\deg r(x) < \deg g(x)\text{.}\)
Basis: \(S(0)\) is true, for if \(f(x)\) has degree 0, it is a nonzero constant, \(f(x)=c\neq 0,\) and so either \(f(x) =g(x)\cdot 0 + c\) if \(g(x)\) is not a constant, or \(f(x) = g(x)g(x)^{-1}+0\) if \(g(x)\) is also a constant.
Induction: Assume that for some \(n\geq 0\text{,}\) \(S(k)\) is true for all \(k \leq n\text{,}\) If \(f(x)\) has degree \(n+1\text{,}\) then there are two cases to consider. If \(\deg g(x) > n + 1\text{,}\) \(f(x) = g(x)\cdot 0 + f(x)\text{,}\) and we are done. Otherwise, if \(\deg g(x) =m \leq n + 1\text{,}\) we perform long division as follows, where LDT’s stand for terms of lower degree than \(n+1\text{.}\)
\begin{equation*}
\begin{array}{rll}
& f_{n+1}\cdot g_m{}^{-1}x^{n+1-m} \\
g_mx^m+ \textrm{ LDT}'s & \overline{\left) f_{n+1}x^{n+1}\right.+ \textrm{ LDT}'s
\textrm{ }}& \\ & \underline{\textrm{ }f_{n+1}x^{n+1}+ \textrm{ LDT}'s}\textrm{
}\\& \quad\quad\quad\quad\quad h(x) \\
\end{array}
\end{equation*}
Therefore,
\begin{equation*}
h(x) = f(x)-\left(f_{n+1}\cdot g_m{}^{-1}x^{n+1-m}\right) g(x) \Rightarrow \textrm{ }f(x) = \left(f_{n+1}\cdot g_m{}^{-1}x^{n+1-m}\right)
g(x)+h(x)
\end{equation*}
Since \(\deg h(x)\) is less than \(n+1\text{,}\) we can apply the induction hypothesis: \(h(x) = g(x)q(x) + r(x)\) with \(\deg r(x) < \deg g(x)\text{.}\)
Therefore,
\begin{equation*}
f(x) = g(x)\left(f_{n+1}\cdot g_m{}^{-1}x^{n+1-m}+ q(x)\right) + r(x)
\end{equation*}
with \(\deg r(x) < \deg g(x)\text{.}\) This establishes the existence of a quotient and remainder. The uniqueness of \(q(x)\) and \(r(x)\) as stated in the theorem is proven as follows: if \(f(x)\) is also equal to \(g(x)\bar{q}(x) + \bar{r}(x)\) with deg \(\bar{r}(x) < \deg g(x)\text{,}\) then
\begin{equation*}
g(x)q(x) + r(x) = g(x) \bar{q}(x) +\overline{ r}(x) \Rightarrow g(x) \left(\bar{q}(x)-q(x)\right)= r(x)-\bar{r}(x)
\end{equation*}
Since \(\deg r(x) - \bar{r}(x) < \deg g(x)\text{,}\) the degree of both sides of the last equation is less than \(\deg g(x)\text{.}\) Therefore, it must be that \(\bar{q}(x) - q(x) = 0\text{,}\) or \(q(x) =\bar{q}(x)\) And so \(r(x) = \bar{r}(x)\text{.}\)
16.4 Field Extensions
Exercises
16.4.1.
Answer.
If \(a_0+ a_1\sqrt{2}\in \mathbb{Q}\left[\sqrt{2}\right]\) is nonzero, then it has a multiplicative inverse:
\begin{equation*}
\begin{split}
\frac{1}{a_0+ a_1\sqrt{2}} &=\frac{1}{a_0+ a_1\sqrt{2}}\frac{a_0- a_1\sqrt{2}}{a_0- a_1\sqrt{2}}\quad\\
& =\frac{a_0- a_1\sqrt{2}}{a_0{}^2- 2a_1{}^2}\\
& =\frac{a_0}{a_0{}^2- 2a_1{}^2}-\frac{ a_1}{a_0{}^2- 2a_1{}^2}\sqrt{2}
\end{split}
\end{equation*}
The denominator, \(a_0{}^2- 2a_1{}^2\text{,}\) is nonzero since \(\sqrt{2}\) is irrational. Since \(\frac{a_0}{a_0{}^2- 2a_1{}^2}\) and\(\frac{-a_1}{a_0{}^2-
2a_1{}^2}\) are both rational numbers, \(a_0+ a_1\sqrt{2}\) is a unit of \(\mathbb{Q}\left[\sqrt{2}\right]\text{.}\) The field containing \(\mathbb{Q}\left[\sqrt{2}\right]\) is denoted \(\mathbb{Q}\left(\sqrt{2}\right)\) and so \(\mathbb{Q}\left(\sqrt{2}\right)=\mathbb{Q}\left[\sqrt{2}\right]\)
16.4.3.
Answer.
\(\mathbb{Q}(\sqrt{2}) = \{a + b\sqrt{2} \mid a, b \in \mathbb{Q}\}\) contains the zeros \(\pm \sqrt{2}\) but does not contain \(\pm \sqrt{3}\text{,}\) since neither are expressible in the form \(a + b\sqrt{2}\text{.}\) If we consider the set \(\{c + d\sqrt{3} \mid c,d \in \mathbb{Q}(\sqrt{2})\}\text{,}\) then this field contains \(\pm \sqrt{3}\) as well as \(\pm \sqrt{2}\text{,}\) and is denoted \(\mathbb{Q}(\sqrt{2})(\sqrt{3})= \mathbb{Q}(\sqrt{2}, \sqrt{3})\text{.}\) Taking into account the form of \(c\) and \(d\) in the description above, we can expand to
\begin{equation*}
\mathbb{Q}(\sqrt{2},\sqrt{3})= \{b_0 + b_1\sqrt{2} + b_2 \sqrt{3} +b_3\sqrt{6} \mid b_i \in \mathbb{Q}\}
\end{equation*}
16.4.5.
Answer.
-
\(f(x) = x^3 + x + 1\) is reducible if and only if it has a factor of the form \(x- a\text{.}\) By Theorem 16.3.14, \(x-a\) is a factor if and only if \(a\) is a zero. Neither 0 nor 1 is a zero of \(f(x)\) over \(\mathbb{Z}_2\text{.}\)
-
Since \(f(x)\) is irreducible over \(\mathbb{Z}_2\text{,}\) all zeros of \(f(x)\) must lie in an extension field of \(\mathbb{Z}_2\) . Let c be a zero of \(f(x)\text{.}\) \(\mathbb{Z}_2(c)\) can be described several different ways. One way is to note that since \(c \in \mathbb{Z}_2(c)\text{,}\) \(c^n\in \mathbb{Z}_2(c)\) for all n. Therefore, \(\mathbb{Z}_2(c)\) includes 0, \(c\text{,}\) \(c^2\text{,}\) \(c^3, \ldots\text{.}\) But \(c^3 = c + 1\) since \(f(c) = 0\text{.}\) Furthermore, \(c^4 = c^2+ c\text{,}\) \(c^5= c^2+ c +1\text{,}\) \(c^6= c^2+1\text{,}\) and \(c^7=1\text{.}\) Higher powers of \(c\) repeat preceding powers. Therefore,\begin{equation*} \begin{split} \mathbb{Z}_2(c)&= \left\{0, 1, c, c^2 , c + 1, c^2 + 1, c^2 + c + 1, c ^2 + c\right\}\\ &= \left\{a_0+ a_1c+a_2c^2 \mid a_i\in \mathbb{Z}_2\right\}\\ \end{split} \end{equation*}The three zeros of \(f(x)\) are \(c\text{,}\) \(c^2\) and \(c^2+ c\text{.}\)\begin{equation*} f(x) = (x + c)\left(x+ c ^2 \right)\left(x + c^2 + c\right) \end{equation*}
-
Cite Theorem Theorem 16.2.10, part 3.
16.5 Power Series
16.5.3 Exercises
16.5.3.5.
Answer.
-
\begin{equation*} \begin{array}{c} b_0= 1\\ b_1=(-1)(2\cdot 1) = -2\\ b_2=(-1)(2\cdot (-2)+4\cdot 1)= 0\\ b_3= (-1)(2\cdot 0 + 4\cdot (-2)+8\cdot 1)=0\\ \end{array} \end{equation*}All other terms are zero. Hence, \(f(x)^{-1}= 1-2x\)
-
\begin{equation*} \begin{split} f(x) &=1+2x + 2^2x^2+ 2^3x^3+ \cdots \\ &=(2x)^0 + (2x)^1 + (2x)^2+ (2x)^3+\cdots \\ &= \frac{1}{1-2x}\\ \end{split} \end{equation*}The last step follows from the formula for the sum of a geometric series.
16.5.3.7.
Answer.
-
\begin{equation*} \begin{split} \left(x^4-x^5\right)^{-1} & =(x^4 (1-x))^{-1}\\ &=x^{-4}\frac{1}{1-x}\\ & =x^{-4}\left(\sum_{k=0}^{\infty } x^k\right)\\ &=\sum_{k=-4}^{\infty} x^k\\ \end{split}\text{.} \end{equation*}
-
\begin{equation*} \begin{split} \left(x^4-2 x^3+x^2\right)^{-1} & =\left(x^2 \left(x^2-2 x+1\right)\right)^{-1}\\ &=x^{-2}\left(1-2x+x^2\right)^{-1}\\ & =x^{-2}\left(\sum_{k=0}^{\infty } (k+1) x^k\right)\\ &=\sum_{k=-2}^{\infty} (k+2) x^k\\ \end{split}\text{.} \end{equation*}