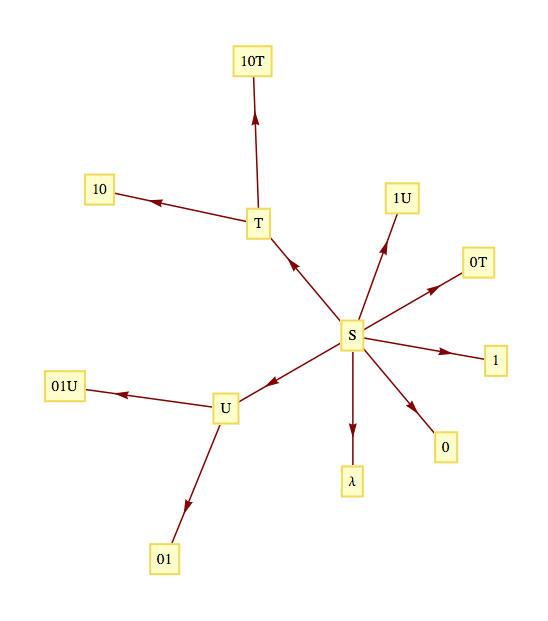
Case 1. Given the alphabet
\(B=\{0,1\}\text{,}\) we can define a bijection from the positive integers into
\(B^*\text{.}\) Each positive integer has a binary expansion
\(d_kd_{k-1}\cdots d_1d_0\text{,}\) where each
\(d_j\) is 0 or 1 and
\(d_k=1\text{.}\) If
\(n\) has such a binary expansion, then
\(2^k \leq n\leq 2^{k+1}\text{.}\) We define
\(f:\mathbb{P}\to B^*\) by
\(f(n)=f\left(d_kd_{k-1}\cdots d_1d_0\right)=d_{k-1}\cdots d_1d_0,\) where
\(f(1)=\lambda\text{.}\) Every one of the
\(2^k\) strings of length
\(k\) are the images of exactly one of the integers between
\(2^k\textrm{ and } 2^{k+1}-1.\) From its definition,
\(f\) is clearly a bijection; therefore,
\(B^*\) is countable.
Case 2:
\(A\) is Finite. We will describe how this case is handled with an example first and then give the general proof. If
\(A=\{a,b,c,d,e\}\text{,}\) then we can code the letters in
\(A\) into strings from
\(B^3\text{.}\) One of the coding schemes (there are many) is
\(a\leftrightarrow 000, b\leftrightarrow
001, c\leftrightarrow 010, d\leftrightarrow 011, \textrm{ and } e\leftrightarrow 100\text{.}\) Now every string in
\(A^*\) corresponds to a different string in
\(B^*\text{;}\) for example,
\(ace\text{.}\) would correspond with
\(000010100\text{.}\) The cardinality of
\(A^*\) is equal to the cardinality of the set of strings that can be obtained from this encoding system. The possible coded strings must be countable, since they are a subset of a countable set,
\(B^*\text{.}\) Therefore,
\(A^*\) is countable.
If
\(\lvert A\rvert =m\text{,}\) then the letters in
\(A\) can be coded using a set of fixed-length strings from
\(B^*\text{.}\) If
\(2^{k-1} < m \leq 2^k\text{,}\) then there are at least as many strings of length
\(k\) in
\(B^k\) as there are letters in
\(A\text{.}\) Now we can associate each letter in
\(A\) with with a different element of
\(B^k\text{.}\) Then any string in
\(A^*\text{.}\) corresponds to a string in
\(B^*\text{.}\) By the same reasoning as in the example above,
\(A^*\) is countable.
Case 3:
\(A\) is Countably Infinite. We will leave this case as an exercise.