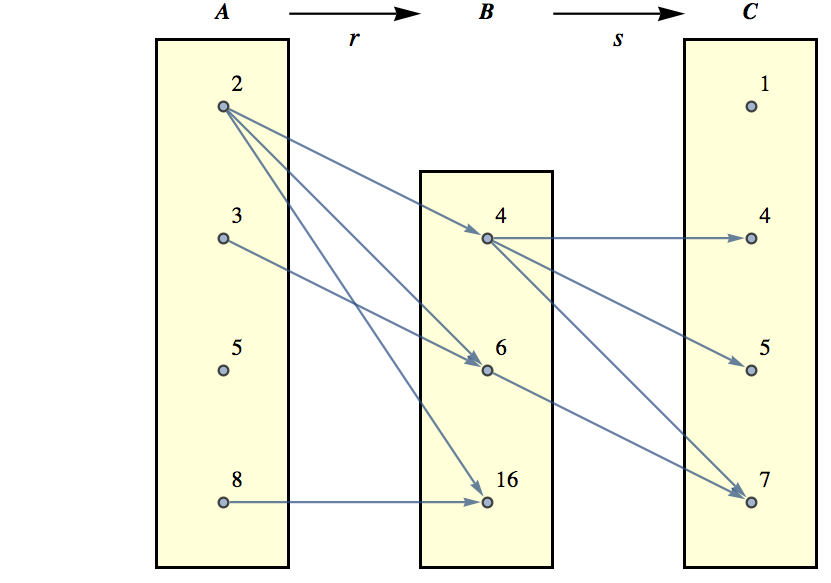
Definition 6.1.1. Relation.
Let \(A\) and \(B\) be sets. A relation from \(A\) into \(B\) is any subset of \(A\times B\text{.}\)
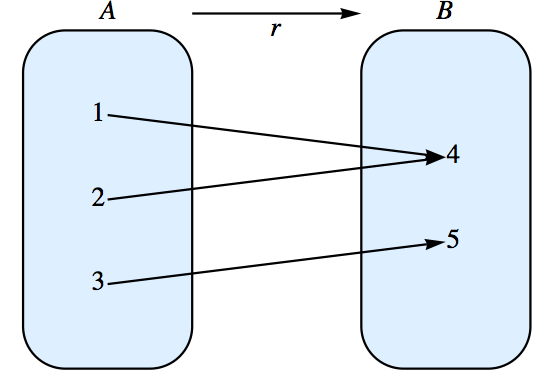
| \(2 | 4 \textrm{ and } 4 \leq 4\) |
| \(2 | 4 \textrm{ and } 4 \leq 5\) |
| \(2 | 4 \textrm{ and } 4 \leq 7\) |
| \(2| 6 \textrm{ and } 6 \leq 7\) |
| \(3| 6 \textrm{ and } 6 \leq 7\) |