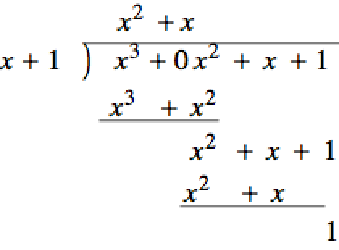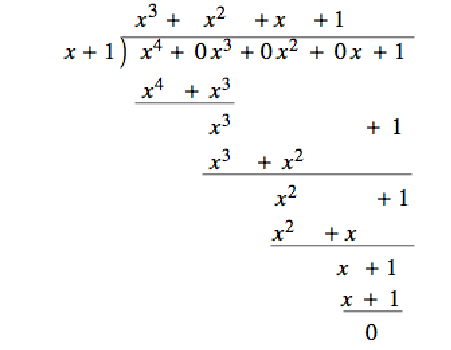Skip to main content
Logo image

Applied Discrete Structures

Al Doerr, Ken Levasseur

Section 16.3 Polynomial Rings

In the previous sections we examined the solutions of a few equations over different rings and fields. To solve the equation \(x^2- 2 = 0\) over the field of the real numbers means to find all solutions of this equation that are in this particular field \(\mathbb{R}\text{.}\) This statement can be replaced as follows: Determine all \(a \in \mathbb{R}\) such that the polynomial \(f(x) = x^2 - 2\) is equal to zero when evaluated at \(x=a\text{.}\) In this section, we will concentrate on the theory of polynomials. We will develop concepts using the general setting of polynomials over rings since results proven over rings are true for fields (and integral domains). The reader should keep in mind that in most cases we are just formalizing concepts that he or she learned in high school algebra over the field of reals.
🔗

Definition 16.3.1. Polynomial over a Ring.

Let \([R; +, \cdot ]\) be a ring. A polynomial, \(f(x)\text{,}\) over \(R\) is an expression of the form
\begin{equation*} f(x)=\sum _{i=0}^n a_i x^i=a_0 + a_1 x+a_2 x^2+ \cdots +a_n x^n \end{equation*}
where \(n\geq 0\text{,}\) and \(a_0, a_1, a_2, \ldots, a_n \in R\text{.}\) If \(a_n \neq 0\text{,}\) then the degree of \(f(x)\) is \(n\text{.}\) If \(f(x) = 0\text{,}\) then the degree of \(f(x)\) is undefined, but for convenience we say that \(\deg 0 = -\infty\text{.}\) If the degree of \(f(x)\) is \(n\text{,}\) we write \(\deg f(x) = n\text{.}\) The set of all polynomials in the indeterminate \(x\) with coefficients in \(R\) is denoted by \(R[x]\text{.}\)
🔗
🔗

Note 16.3.2.

  • The symbol \(x\) is an object called an indeterminate, which is not an element of the ring \(R\text{.}\)
    🔗
    🔗
  • Note that \(R\subseteq R[x]\text{.}\) The elements of \(R\) are called constant polynomials, with the nonzero elements of \(R\) being the polynomials of degree 0.
    🔗
    🔗
  • \(R\) is called the ground, or base, ring for \(R[x]\text{.}\)
    🔗
    🔗
  • In the definition above, we have written the terms in increasing degree starting with the constant. The ordering of terms can be reversed without changing the polynomial. For example, \(1 + 2 x -3x^4\) and \(-3x^4+2 x+1\) are the same polynomial.
    🔗
    🔗
  • A term of the form \(x^k\) in a polynomial is understood to be \(1 x^k\text{.}\)
    🔗
    🔗
  • It is understood that if \(\deg f(x) = n\text{,}\) then coefficients of powers of \(x\) higher than \(n\) are equal to the zero of the base ring.
    🔗
    🔗
🔗
🔗

Definition 16.3.3. Polynomial Addition.

Let \(f(x) =a_0 + a_1 x+a_2 x^2+ \cdots +a_m x^m\) and \(g(x) =b_0 + b_1 x+b_2 x^2+ \cdots +b_n x^n\) be elements in \(R[x]\) so that \(a_i \in R\) and \(b_i\in R\) for all i. Let \(k\) be the maximum of \(m\) and \(n\text{.}\) Then \(f(x) + g(x) =c_0 + c_1 x+c_2 x^2+ \cdots +c_k x^k\text{,}\) where \(c_i=a_i+b_i\) for \(i = 0, 1, 2, \ldots , k\text{.}\)
🔗
🔗

Definition 16.3.4. Polynomial Multiplication.

Let \(f(x) =a_0 + a_1 x+a_2 x^2+ \cdots +a_m x^m\) and \(g(x) =b_0 + b_1 x+b_2 x^2+ \cdots +b_n x^n\text{.}\) Then
\begin{equation*} \begin{array}{c} f(x) \cdot g(x) = d_0 + d_1 x+d_2 x^2+ \cdots +d_p x^p \quad \textrm{ where } p=m+n \textrm{ and }\\ d_s=\sum_{i=0}^s a_i b_{s-i} =a_0 b_s+a_1 b_{s-1}+a_2 b_{s-2}+\cdots +a_{s-1} b_1+a_s b_0\\ \textrm{for } 0\leq s\leq p\\ \\ \end{array} \end{equation*}
🔗
🔗
The important fact to keep in mind is that addition and multiplication in \(R[x]\) depends on addition and multiplication in \(R\text{.}\) The powers of \(x\) merely serve the purpose of “place holders.” All computations involving coefficients are done over the given ring. Powers of the indeterminate are computed formally applying the rule of adding exponents when multiplying powers.
🔗

Example 16.3.5.

\(f(x) = 3\text{,}\) \(g(x) = 2 - 4x +7x^2\) , and \(h(x) = 2 + x^4\) are all polynomials in \(\mathbb{Z}[x]\text{.}\) Their degrees are 0, 2, and 4, respectively.
🔗
🔗
Addition and multiplication of polynomials are performed as in high school algebra. However, we must do our computations in the ground ring of the polynomials.
🔗

Example 16.3.6.

In \(\mathbb{Z}_3[x]\text{,}\) if \(f(x) = 1+x\) and \(g(x) = 2+x\text{,}\) then
\begin{equation*} \begin{split} f(x) + g(x) &= (1+x) + (2+x)\\ & = \left(1 +_3 2\right)+ \left(1 +_3 1\right) x\\ & = 0 + 2x \\ & = 2x \end{split} \end{equation*}
and
\begin{equation*} \begin{split} f(x)g(x) &= (1+x) \cdot (2 +x) \\ &= 1\times_3 2+ (1 \times_3 1 +_3 1 \times_3 2)x + (1 \times_3 1)x^2\\ & =2 + 0 x + x^2\\ & =2 + x^2\\ \end{split} \end{equation*}
However, for the same polynomials as above, \(f(x)\) and \(g(x)\) in the more familiar setting of \(\mathbb{Z}[x]\text{,}\) we have
\begin{equation*} f(x) + g(x) = (1+x) + (2+x) = (1 +2)+ (1 +1) x = 3 + 2x \end{equation*}
and
\begin{equation*} \begin{split}f(x)g(x) =(1+x)\cdot(2 +x)\\ & = 1\cdot 2+ (1 \cdot 1 + 1 \cdot 2)x + (1 \cdot 1)x^2\\ & = 2 +3x + x^2\\ \end{split} \end{equation*}
🔗
🔗

Example 16.3.7.

Let \(f(x) = 2 + x^2\) and \(g(x) = -1 + 4x + 3x^2\text{.}\) We will compute \(f(x) \cdot g(x)\) in \(\mathbb{Z}[x]\text{.}\) Of course this product can be obtained by the usual methods of high school algebra. We will, for illustrative purposes, use the above definition. Using the notation of the above definition, \(a_0=2\text{,}\) \(a_1=0\text{,}\) \(a_2=1\text{,}\) \(b_0=-1\text{,}\) \(b_1= 4\text{,}\) and \(b_2 = 3\text{.}\) We want to compute the coefficients \(d_0\text{,}\) \(d_1\text{,}\) \(d_2\text{,}\) \(d_3\text{,}\) and \(d_4\) . We will compute \(d_3\) , the coefficient of the \(x^3\) term of the product, and leave the remainder to the reader (see Exercise 2 of this section). Since the degrees of both factors is 2, \(a_i= b_i= 0\) for \(i\geq 3\text{.}\) The coefficient of \(x^3\) is
\begin{equation*} d_3=a_0 b_3+a_1 b_2+a_2 b_1+a_3b_0 =2\cdot 0+0\cdot 3+1\cdot 4+0\cdot (-1)=4 \end{equation*}
🔗
🔗
The proofs of the following theorem are not difficult but rather long, so we omit them.
🔗
Next we turn to division of polynomials, which is not an operation since the result is a pair of polynomials, not a single one. From high school algebra we all learned the standard procedure for dividing a polynomial \(f(x)\) by a second polynomial \(g(x)\text{.}\) This process of polynomial long division is referred to as the division property for polynomials. Under this scheme we continue to divide until the result is a quotient \(q(x)\) and a remainder \(r(x)\) whose degree is strictly less than that of the divisor \(g(x)\text{.}\) This property is valid over any field. Before giving a formal description, we consider some examples.
🔗

Example 16.3.9. Polynomial Division.

Let \(f(x) = 1 + x + x^3\) and \(g(x) = 1 + x\) be two polynomials in \(\mathbb{Z}_2[x]\text{.}\) Let us divide \(f(x)\) by \(g(x)\text{.}\) Keep in mind that we are in \(\mathbb{Z}_2[x]\) and that, in particular, \(-1=1\) in \(\mathbb{Z}_2\) . This is a case where reordering the terms in decreasing degree is preferred.
🔗
described in detail following the image
fig-poly-divison-1
🔗
Figure 16.3.10.
🔗
Therefore,
\begin{equation*} \frac{x^3 + x + 1}{x+ 1}= x^2+ x + \frac{1}{x + 1} \end{equation*}
or equivalently,
\begin{equation*} x^3 + x + 2= \left( x^2+ x\right)\cdot (x+1) + 1 \end{equation*}
That is, \(f(x) = g(x)\cdot q(x) + r(x)\) where \(q(x) = x^2+x\) and \(r(x) = 1\text{.}\) Notice that \(\deg (r(x)) = 0\text{,}\) which is strictly less than \(\deg (g(x)) = 1\text{.}\)
🔗
🔗

Example 16.3.11.

Let \(f(x) = 1 +x^4\) and \(g(x) = 1 + x\) be polynomials in \(\mathbb{Z}_2[x]\text{.}\) Let us divide \(f(x)\) by \(g(x)\text{:}\)
🔗
described in detail following the image
fig-poly-divison-2
🔗
Figure 16.3.12.
🔗
Thus \(x^4+ 1 = \left(x^3+x^2+ x + 1\right)(x+1) \text{.}\) Since we have 0 as a remainder, \(x + 1\) must be a factor of \(x^4+ 1\text{.}\) Also, since \(x + 1\) is a factor of \(x^4 + 1\text{,}\) 1 is a zero (or root) of \(x^4 + 1\text{.}\) Of course we could have determined that 1 is a root of \(f(x)\) simply by computing \(f(1) =1^4 +_2 1 = 1 +_2 1 = 0\text{.}\)
🔗
🔗
Before we summarize the main results suggested by the previous examples, we should probably consider what could have happened if we had attempted to perform divisions of polynomials in the ring \(\mathbb{Z}[x]\) rather than in the polynomials over the field \(\mathbb{Z}_2\text{.}\) For example, \(f(x) = x^2 - 1\) and \(g(x) = 2x - 1\) are both elements of the ring \(\mathbb{Z}[x]\text{,}\) yet \(x^2-1=(\frac{1}{2} x+\frac{1}{2})(2x-1)-\frac{3}{4}\) The quotient and remainder are not a polynomials over \(\mathbb{Z}\) but polynomials over the field of rational numbers. For this reason it would be wise to describe all results over a field \(F\) rather than over an arbitrary ring \(R\) so that we don’t have to expand our possible set of coefficients.
🔗

Proof.

This theorem can be proven by induction on \(\deg f(x)\text{.}\)
🔗
🔗

Proof.

(⇒) 

Assume that \(a \in F\) is a zero of \(f(x) \in F[x]\text{.}\) We wish to show that \(x - a\) is a factor of \(f(x)\text{.}\) To do so, apply the division property to \(f(x)\) and \(g(x) = x - a\text{.}\) Hence, there exist unique polynomials \(q(x)\) and \(r(x)\) from \(F[x]\) such that \(f(x) = (x - a)\cdot q(x) + r(x)\) and the \(\deg r(x) < \deg(x - a) = 1\text{,}\) so \(r (x) = c \in F\text{,}\) that is, \(r(x)\) is a constant. Also, the fact that \(a\) is a zero of \(f(x)\) means that \(f(a) = 0\text{.}\) So \(f(x) = (x - a)\cdot q(x) + c\) becomes \(0 = f(a) = (a - a) q(a) + c\text{.}\) Hence \(c = 0\text{,}\) so \(f(x) = (x - a) \cdot q(x)\text{,}\) and \(x - a\) is a factor of \(f(x)\text{.}\) The reader should note that a critical point of the proof of this half of the theorem was the part of the division property that stated that \(\deg r(x) < \deg g(x)\text{.}\)
🔗
🔗

(⇐) 

We leave this half to the reader as an exercise.
🔗
🔗
🔗

Proof.

Let \(a \in F\) be a zero of \(f(x)\text{.}\) Then \(f(x) = (x - a) \cdot q_1(x)\text{,}\) \(q_1(x)\in F[x]\text{,}\) by the Factor Theorem. If \(b \in F\) is a zero of \(q_1(x)\text{,}\) then again by Factor Theorem, \(f(x) = (x -a)(x - b)q_2(x)\text{,}\) \(q_2(x)\in F[x]\text{.}\) Continue this process, which must terminate in at most \(n\) steps since the degree of \(q_k(x)\) would be \(n-k\text{.}\)
🔗
🔗
From The Factor Theorem, we can get yet another insight into the problems associated with solving polynomial equations; that is, finding the zeros of a polynomial. The initial important idea here is that the zero \(a\) is from the ground field \(F\text{.}\) Second, \(a\) is a zero only if \((x - a)\) is a factor of \(f(x)\) in \(F[x]\text{;}\) that is, only when \(f(x)\) can be factored (or reduced) to the product of \((x - a)\) times some other polynomial in \(F[x]\text{.}\)
🔗

Example 16.3.16.

Consider the polynomial \(f(x) = x^2-2\) taken as being in \(\mathbb{Q}\)[x]. From high school algebra we know that \(f(x)\) has two zeros (or roots), namely \(\pm \sqrt{2}\text{,}\) and \(x^2 - 2\) can be factored as \(\left(x - \sqrt{2}\right) \left(x + \sqrt{2}\right)\text{.}\) However, we are working in \(\mathbb{Q}[x]\text{,}\) these two factors are not in the set of polynomials over the rational numbers, \(\mathbb{Q}\) since \(\sqrt{2} \notin \mathbb{Q}\) . Therefore, \(x^2 - 2\) does not have a zero in \(\mathbb{Q}\) since it cannot be factored over \(\mathbb{Q}\text{.}\) When this happens, we say that the polynomial is irreducible over \(\mathbb{Q}\text{.}\)
🔗
🔗
The problem of factoring polynomials is tied hand-in-hand with that of the reducibility of polynomials. We give a precise definition of this concept.
🔗

Definition 16.3.17. Reducibility over a Field.

Let \([F; +, \cdot]\) be a field and let \(f(x) \in F[x]\) be a nonconstant polynomial. \(f(x)\) is reducible over \(F\) if and only if it can be factored as a product of two nonconstant polynomials in \(F[x]\text{.}\) A polynomial is irreducible over \(F\) if it is not reducible over \(F\text{.}\)
🔗
🔗

Example 16.3.18.

The polynomial \(f(x) = x^4 + 1\) is reducible over \(\mathbb{Z}_2\) since \(x^4 + 1 = (x + 1)\left(x^3 + x^2 + x - 1\right).\)
🔗
🔗

Example 16.3.19.

Is the polynomial \(f(x) = x^3 + x + 1\) reducible over \(\mathbb{Z}_2\text{?}\) Since a factorization of a cubic polynomial can only be as a product of linear and quadratic factors, or as a product of three linear factors, \(f(x)\) is reducible if and only if it has at least one linear factor. From the Factor Theorem, \(x - a\) is a factor of \(x^3 + x + 1\) over \(\mathbb{Z}_2\) if and only if \(a \in \mathbb{Z}_2\) is a zero of \(x^3 + x + 1\text{.}\) So \(x^3 + x + 1\) is reducible over \(\mathbb{Z}_2\) if and only if it has a zero in \(\mathbb{Z}_2\) . Since \(\mathbb{Z}_2\) has only two elements, 0 and 1, this is easy enough to check. \(f(0) = 0^3 +_2 0+_2 1= 1\) and \(f(1) =1^3 +_2 1 +_2 1 = 1\text{,}\) so neither 0 nor 1 is a zero of \(f(x)\) over \(\mathbb{Z}_2\text{.}\) Hence, \(x^3 + x + 1\) is irreducible over \(\mathbb{Z}_2\text{.}\)
🔗
🔗
From high school algebra we know that \(x^3 + x + 1\) has three zeros from some field. Can we find this field? To be more precise, can we construct the field that contains \(\mathbb{Z}_2\) and all zeros of \(x^3 + x + 1\text{?}\) We will consider this task in the next section.
🔗
We close this section with a final analogy. Prime numbers play an important role in mathematics. The concept of irreducible polynomials (over a field) is analogous to that of a prime number. Just think of the definition of a prime number. A useful fact concerning primes is: If \(p\) is a prime and if \(p \mid a b\text{,}\) then \(p \mid a\) or \(p \mid b\text{.}\) We leave it to the reader to think about the veracity of the following: If \(p(x)\) is an irreducible polynomial over \(F\text{,}\) \(a(x), b(x) \in F[x]\) and \(p(x) \mid a(x) b(x)\text{,}\) then \(p(x) \mid a(x)\) or \(p(x) \mid b(x)\text{.}\)
🔗

Exercises Exercises

1.

Let \(f(x) = 1 + x\) and \(g(x) = 1 + x + x^2\text{.}\) Compute the following sums and products in the indicated rings.
  1. \(f(x) + g(x)\) and \(f(x) \cdot g(x)\) in \(\mathbb{Z}[x]\)
    🔗
    🔗
  2. \(f(x) + g(x)\) and \(f(x) \cdot g(x)\) in \(\mathbb{Z}_2[x]\)
    🔗
    🔗
  3. \((f(x)\cdot g(x))\cdot f(x)\) in \(\mathbb{Q}[x]\)
    🔗
    🔗
  4. \((f(x) \cdot g(x)) \cdot f(x)\) in \(\mathbb{Z}_2[x]\)
    🔗
    🔗
  5. \(f(x) \cdot f(x) + f(x)\cdot g(x)\) in \(\mathbb{Z}_2[x]\)
    🔗
    🔗
🔗
Answer.
  1. \(f(x) + g(x) = 2 + 2x + x^2\) , \(f(x)\cdot g(x) =1 +2x +2x^2+x^3\)
    🔗
    🔗
  2. \(f(x)+g(x)=x^2\text{,}\) \(f(x)\cdot g(x) =1+x^3\)
    🔗
    🔗
  3. \(\displaystyle 1 + 3x + 4x ^2 + 3x^3 + x^4\)
    🔗
    🔗
  4. \(\displaystyle 1 + x + x^3 + x^4\)
    🔗
    🔗
  5. \(\displaystyle x^2+ x^3\)
    🔗
    🔗
🔗
🔗
🔗

3.

Prove that:
  1. The ring \(\mathbb{R}\) is a subring of the ring \(\mathbb{R}[x]\text{.}\)
    🔗
    🔗
  2. The ring \(\mathbb{Z}[x]\) is a subring of the \(\mathbb{Q}[x]\text{.}\)
    🔗
    🔗
  3. The ring \(\mathbb{Q}[x]\) is a subring of the ring \(\mathbb{R}[x]\text{.}\)
    🔗
    🔗
🔗
Answer.
  1. If \(a, b \in \mathbb{R}\text{,}\) \(a - b\) and \(a b\) are in \(\mathbb{R}\) since \(\mathbb{R}\) is a ring in its own right. Therefore, \(\mathbb{R}\) is a subring of \(\mathbb{R}[x]\text{.}\) The proofs of parts b and c are similar.
    🔗
    🔗
🔗
🔗
🔗

4.

  1. Find all zeros of \(x^4+ 1\) in \(\mathbb{Z}_3\text{.}\)
    🔗
    🔗
  2. Find all zeros of \(x^5 + 1\) in \(\mathbb{Z}_5\text{.}\)
    🔗
    🔗
🔗
🔗

5.

Determine which of the following are reducible over \(\mathbb{Z}_2\text{.}\) Explain.
  1. \(\displaystyle f(x) = x^3 + 1\)
    🔗
    🔗
  2. \(g(x) = x^3 + x^2 + x\text{.}\)
    🔗
    🔗
  3. \(h(x) = x^3+ x^2 + 1\text{.}\)
    🔗
    🔗
  4. \(k(x) = x^4 +x^2+ 1\text{.}\) (Be careful.)
    🔗
    🔗
🔗
Answer.
  1. Reducible, \((x+1)\left(x^2+ x+1\right)\)
    🔗
    🔗
  2. Reducible, \(x\left(x^2+x+1\right)\)
    🔗
    🔗
  3. Irreducible. If you could factor this polynomial, one factor would be either \(x\) or \(x + 1\text{,}\) which would give you a root of 0 or 1, respectively. By substitution of 0 and 1 into this polynomial, it clearly has no roots.
    🔗
    🔗
  4. Reducible, \((x+1)^{4 }\)
    🔗
    🔗
🔗
🔗
🔗

7.

Give an example of the contention made in the last paragraph of this section.
🔗
Answer.
We illustrate this property of polynomials by showing that it is not true for a nonprime polynomial in \(\mathbb{Z}_2[x]\text{.}\) Suppose that \(p(x) = x^2+ 1\text{,}\) which can be reduced to \((x+1)^2\) , \(a(x) = x^2 + x\text{,}\) and \(b(x) = x^3 + x^2\text{.}\) Since \(a(x)b(x) =x^5+x^3= x^3\left(x^2+1\right)\text{,}\) \(p(x)|a(x)b(x)\text{.}\) However, \(p(x)\) is not a factor of either \(a(x)\) or \(b(x)\text{.}\)
🔗
🔗
🔗

8.

Determine all zeros of \(x^4+ 3x^3 + 2x + 4\) in \(\mathbb{Z}_5[x]\text{.}\)
🔗
🔗

9.

Show that \(x^2 - 3\) is irreducible over \(\mathbb{Q}\) but reducible over the field of real numbers.
🔗
Answer.
The only possible proper factors of \(x^2- 3\) are \(\left(x - \sqrt{3}\right)\) and \(\left(x+\sqrt{3}\right)\text{,}\) which are not in \(\mathbb{Q}[x]\) but are in \(\mathbb{R}\)[x].
🔗
🔗
🔗

10.

The definition of a vector space given in Chapter 13 holds over any field \(F\text{,}\) not just over the field of real numbers, where the elements of \(F\) are called scalars.
  1. Show that \(F[x]\) is a vector space over \(F\text{.}\)
    🔗
    🔗
  2. Find a basis for \(F[x]\) over \(F\text{.}\)
    🔗
    🔗
  3. What is the dimension of \(F[x]\) over \(F\text{?}\)
    🔗
    🔗
🔗
🔗

11.

Prove Theorem 16.3.13, the Division Property for Polynomials
🔗
Answer.
For \(n \geq 0\text{,}\) let \(S(n)\) be the proposition: For all \(g(x)\neq 0\) and \(f(x)\) with \(\deg f(x) = n\text{,}\) there exist unique polynomials \(q(x)\) and \(r(x)\) such that \(f(x)=g(x)q(x)+r(x)\text{,}\) and either \(r(x)=0\) or \(\deg r(x) < \deg g(x)\text{.}\)
🔗
Basis: \(S(0)\) is true, for if \(f(x)\) has degree 0, it is a nonzero constant, \(f(x)=c\neq 0,\) and so either \(f(x) =g(x)\cdot 0 + c\) if \(g(x)\) is not a constant, or \(f(x) = g(x)g(x)^{-1}+0\) if \(g(x)\) is also a constant.
🔗
Induction: Assume that for some \(n\geq 0\text{,}\) \(S(k)\) is true for all \(k \leq n\text{,}\) If \(f(x)\) has degree \(n+1\text{,}\) then there are two cases to consider. If \(\deg g(x) > n + 1\text{,}\) \(f(x) = g(x)\cdot 0 + f(x)\text{,}\) and we are done. Otherwise, if \(\deg g(x) =m \leq n + 1\text{,}\) we perform long division as follows, where LDT’s stand for terms of lower degree than \(n+1\text{.}\)
\begin{equation*} \begin{array}{rll} & f_{n+1}\cdot g_m{}^{-1}x^{n+1-m} \\ g_mx^m+ \textrm{ LDT}'s & \overline{\left) f_{n+1}x^{n+1}\right.+ \textrm{ LDT}'s \textrm{ }}& \\ & \underline{\textrm{ }f_{n+1}x^{n+1}+ \textrm{ LDT}'s}\textrm{ }\\& \quad\quad\quad\quad\quad h(x) \\ \end{array} \end{equation*}
🔗
Therefore,
\begin{equation*} h(x) = f(x)-\left(f_{n+1}\cdot g_m{}^{-1}x^{n+1-m}\right) g(x) \Rightarrow \textrm{ }f(x) = \left(f_{n+1}\cdot g_m{}^{-1}x^{n+1-m}\right) g(x)+h(x) \end{equation*}
Since \(\deg h(x)\) is less than \(n+1\text{,}\) we can apply the induction hypothesis: \(h(x) = g(x)q(x) + r(x)\) with \(\deg r(x) < \deg g(x)\text{.}\)
🔗
Therefore,
\begin{equation*} f(x) = g(x)\left(f_{n+1}\cdot g_m{}^{-1}x^{n+1-m}+ q(x)\right) + r(x) \end{equation*}
with \(\deg r(x) < \deg g(x)\text{.}\) This establishes the existence of a quotient and remainder. The uniqueness of \(q(x)\) and \(r(x)\) as stated in the theorem is proven as follows: if \(f(x)\) is also equal to \(g(x)\bar{q}(x) + \bar{r}(x)\) with deg \(\bar{r}(x) < \deg g(x)\text{,}\) then
\begin{equation*} g(x)q(x) + r(x) = g(x) \bar{q}(x) +\overline{ r}(x) \Rightarrow g(x) \left(\bar{q}(x)-q(x)\right)= r(x)-\bar{r}(x) \end{equation*}
Since \(\deg r(x) - \bar{r}(x) < \deg g(x)\text{,}\) the degree of both sides of the last equation is less than \(\deg g(x)\text{.}\) Therefore, it must be that \(\bar{q}(x) - q(x) = 0\text{,}\) or \(q(x) =\bar{q}(x)\) And so \(r(x) = \bar{r}(x)\text{.}\)
🔗
🔗
🔗

12.

  1. Show that the field \(\mathbb{R}\) of real numbers is a vector space over \(\mathbb{R}\text{.}\) Find a basis for this vector space. What is dim \(\mathbb{R}\) over \(\mathbb{R}\text{?}\)
    🔗
    🔗
  2. Repeat part a for an arbitrary field F.
    🔗
    🔗
  3. Show that \(\mathbb{R}\) is a vector space over \(\mathbb{Q}\text{.}\)
    🔗
    🔗
🔗
🔗
🔗
You have attempted of activities on this page.
🔗
PrevTopNext