4.8. Probability of Connectivity¶
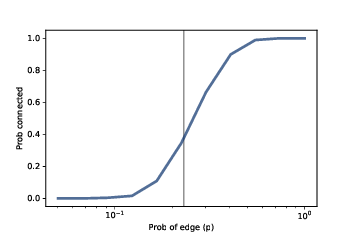
Figure 4.5: Probability of connectivity with n=10 and a range of p. The vertical line shows the predicted critical value.¶
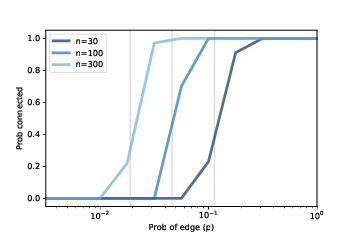
Figure 4.6: Probability of connectivity for several values of n and a range of p.¶
For given values of \(n\) and \(p\), we would like to know the probability that \(G(n, p)\) is connected. We can estimate it by generating a large number of random graphs and counting how many are connected. Here’s how:
def prob_connected(n, p, iters=100):
tf = [is_connected(make_random_graph(n, p))
for i in range(iters)]
return np.mean(bool)
The parameters n and p are passed along to make_random_graph; iters is the number of random graphs we generate.
The result, tf, is a list of boolean values: True for each graph that’s connected and False for each one that’s not.
np.mean is a NumPy function that computes the mean of this list, treating True as 1 and False as 0. The result is the fraction of random graphs that are connected.
>>> prob_connected(10, 0.23, iters=10000)
0.33
We chose 0.23 because it is close to the critical value where the probability of connectivity goes from near 0 to near 1. According to Erdős and Rényi, \(p* = lnn / n = 0.23\).
We can get a clearer view of the transition by estimating the probability of connectivity for a range of values of \(p\):
n = 10
ps = np.logspace(-2.5, 0, 11)
ys = [prob_connected(n, p) for p in ps]
The NumPy function logspace returns an array of \(11\) values from \(10^{−2.5}\) to \(10^0 = 1\), equally spaced on a logarithmic scale.
For each value of p in the array, we compute the probability that a graph with parameter p is connected and store the results in ys.
Figure 4.5 shows the results, with a vertical line at the computed critical value, \(p* = 0.23\). As expected, the transition from 0 to 1 occurs near the critical value.
Figure 4.6 shows similar results for larger values of n. As n increases, the critical value gets smaller and the transition gets more abrupt.
These experimental results are consistent with the analytic results Erdős and Rényi presented in their papers.