4.7. Generating ER Graphs

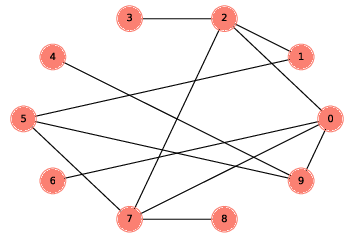
Figure 4.4: An ER graph with n=10 and p=0.3.

The ER graph \(G(n, p)\) contains \(n\) nodes, and each pair of nodes is connected by an edge with probability \(p\). Generating an ER graph is similar to generating a complete graph.

The following generator function enumerates all possible edges and chooses which ones should be added to the graph:

def random_pairs(nodes, p):
for edge in all_pairs(nodes):
    if flip(p):
        yield edge

random_pairs uses flip:

def flip(p):
return np.random.random() < p

This is the first example we’ve seen that uses NumPy. Following convention, we will import numpy as np. NumPy provides a module named random, which provides a method named random, which returns a number between 0 and 1, uniformly distributed.

So flip returns True with the given probability, p, and False with the complementary probability, 1-p.

Finally, make_random_graph generates and returns the ER graph \(G(n, p)\):

def make_random_graph(n, p):
G = nx.Graph()
nodes = range(n)
G.add_nodes_from(nodes)
G.add_edges_from(random_pairs(nodes, p))
return G

make_random_graph is almost identical to make_complete_graph; the only difference is that it uses random_pairs instead of all_pairs.

Here’s an example with \(p=0.3\):

random_graph = make_random_graph(10, 0.3)

Figure 4.4 shows the result. This graph turns out to be connected; in fact, most ER graphs with \(n=10\) and \(p=0.3\) are connected. In the next section, we’ll see how many.

You have attempted of activities on this page