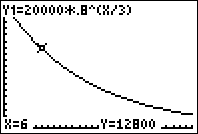Skip to main content
Contents Index Calc Dark Mode Prev Up Next Scratch ActiveCode Profile \(\require{cancel}\newcommand\degree[0]{^{\circ}}
\newcommand\Ccancel[2][black]{\renewcommand\CancelColor{\color{#1}}\cancel{#2}}
\newcommand{\alert}[1]{\boldsymbol{\color{magenta}{#1}}}
\newcommand{\blert}[1]{\boldsymbol{\color{blue}{#1}}}
\newcommand{\bluetext}[1]{\color{blue}{#1}}
\delimitershortfall-1sp
\newcommand\abs[1]{\left|#1\right|}
\newcommand{\lt}{<}
\newcommand{\gt}{>}
\newcommand{\amp}{&}
\newcommand{\fillinmath}[1]{\mathchoice{\boxed{\displaystyle \phantom{\,#1\,}}}{\boxed{\textstyle \phantom{\,#1\,}}}{\boxed{\scriptstyle \phantom{\,#1\,}}}{\boxed{\scriptscriptstyle\phantom{\,#1\,}}}}
\)
Appendix C Answers to Selected Exercises
1 Linear Models 1.1 Creating a Linear Model 1.1.3 Problem Set 1.1
Warm Up 1.1.3.1. 1.1.3.3. Skills Practice 1.1.3.9. Applications 1.1.3.11. Answer .
\(t\) (days)
\(0\) \(5\) \(10\) \(15\) \(20\)
\(h\) (inches)
6
16
26
36
46
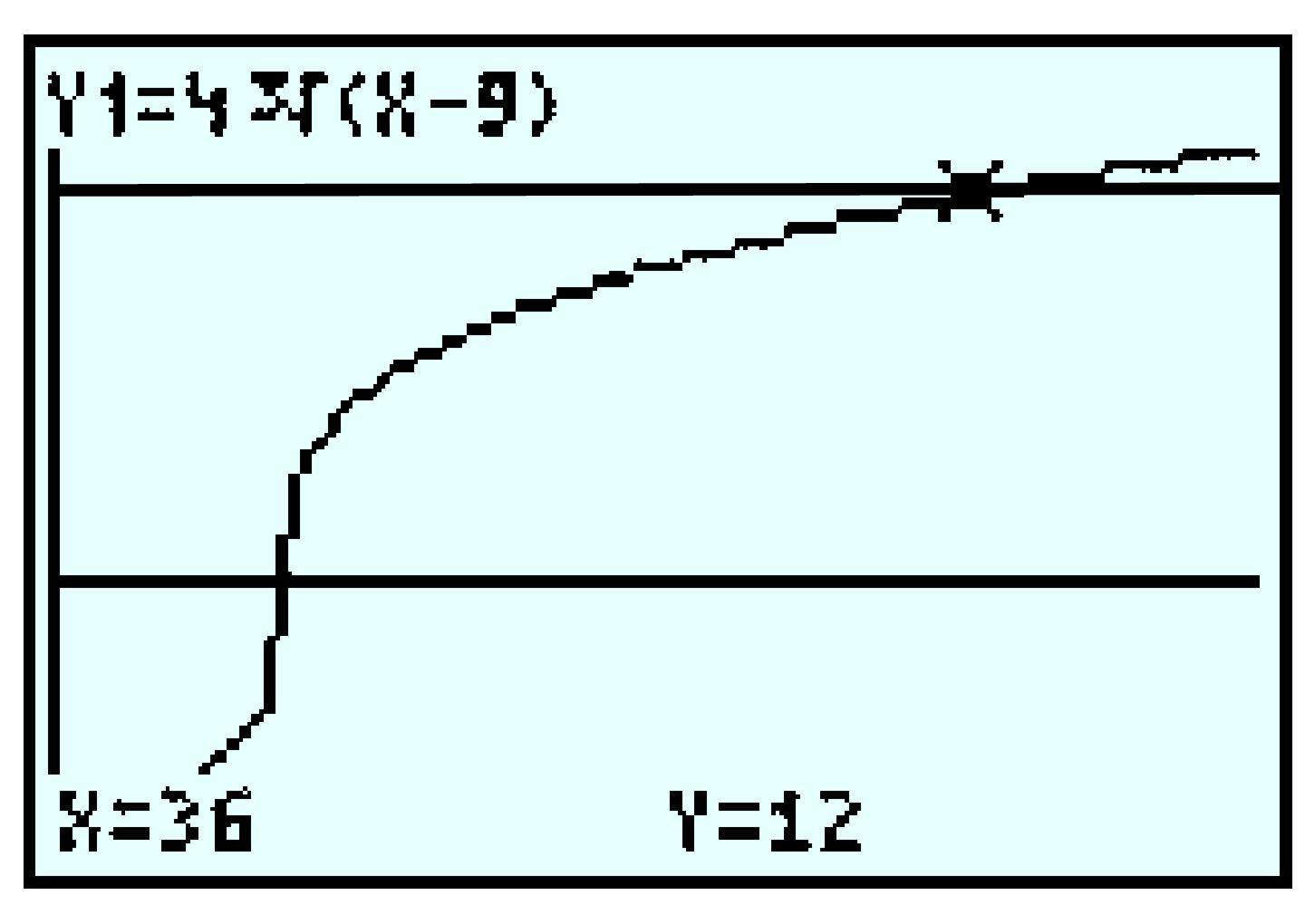
\(h=6+2(21)\text{;}\) \(72=6+2t\)
14 is the initial height of the plants in inches. 1.5 is the number of inches they grow each day.
1.1.3.13. Answer .
Altitude (1000 ft)
\(0\) \(1\) \(2\) \(3\) \(4\) \(5\)
Boiling point (\(\degree\) F)
\(212\) \(210\) \(208\) \(206\) \(204\) \(202\)
\(4\degree\) F
Over 4000 feet
1.2 Graphs and Equations 1.2.6 Problem Set 1.2
Warm Up 1.2.6.7. Answer .
horizontal: 0.25; vertical: 4
1.2.6.9. Answer .
horizontal: 5; vertical: 250
Skills Practice
1.2.6.19. Answer .
\(y = \dfrac{2x}{3} + 24\)
1.2.6.21. Answer .
\(y = \dfrac{-7}{13}x + 7\)
1.2.6.23. Answer .
\(y = \dfrac{2}{9}x + 17\)
Applications 1.2.6.25. Answer .
\(\displaystyle x\lt -6\)
\(\displaystyle x\gt -6\)
\(\displaystyle x\lt -6\)
\(\displaystyle x\gt -6\)
1.2.6.27. Answer .
\(\displaystyle x \le 0.3\)
\(\displaystyle x \ge 0.8\)
1.2.6.29. Answer .
\(\displaystyle x \le 4\)
\(\displaystyle x \gt 2\)
1.2.6.31. Answer .
\(\displaystyle x\lt 22\)
1.2.6.33. Answer .
\(\displaystyle p=120+5t\)
141
7.5 min
1.3 Intercepts 1.3.6 Problem Set 1.3
Warm Up 1.3.6.1. 1.3.6.3. Answer .
\(y=\dfrac{-3}{5}x+\dfrac{16}{5} \)
Skills Practice
1.3.6.5. Answer .
\((4,0) \text{,}\) \((0,-3) \)
1.3.6.7. Answer .
\((-8,0) \text{,}\) \((0,5) \)
1.3.6.9. Answer .
\(\displaystyle (3,0), (0,5) \)
\(\displaystyle \left(\dfrac{1}{2},0\right), \left(0,\dfrac{-1}{4}\right) \)
\(\displaystyle \left(\dfrac{5}{2},0\right), \left(0,\dfrac{-3}{2}\right) \)
\(\displaystyle (p,0), (0,q) \)
The value of
\(a\) is the
\(x\) -intercept, and the value of
\(b\) is the
\(y\) -intercept.
1.3.6.11. Answer .
\(\displaystyle \left(\dfrac{-b}{m},0\right)\)
1.3.6.17. Answer .
\(22x+9y=33\text{,}\) and
\(\displaystyle y = \dfrac{11}{3} + \dfrac{-22}{9}x\)
1.3.6.19. Answer .
\(4x+12y=48\text{,}\) and
\(\displaystyle y = 4 - \dfrac{1}{3}x\)
Applications 1.3.6.21. Answer .
\(\displaystyle 9x+4y=1800\)
\((200,0) \) Delbert must eat 200g of figs daily if he eats no bananas.
\((0,450) \) Delbert must eat 450g of bananas daily if he eats no figs.
1.3.6.23. Answer .
\(~ t ~\) \(0\) \(5\) \(10\) \(15\) \(20\)
\(~ h ~\) \(-400\) \(-300\) \(-200\) \(-100\) \(0\)
\(\displaystyle h=-44+20t \)
\((0,-400) \text{:}\) The diver starts at a depth of 400 feet.
\((20,0) \text{:}\) The diver surfaces after 20 minutes.
1.3.6.25. Answer .
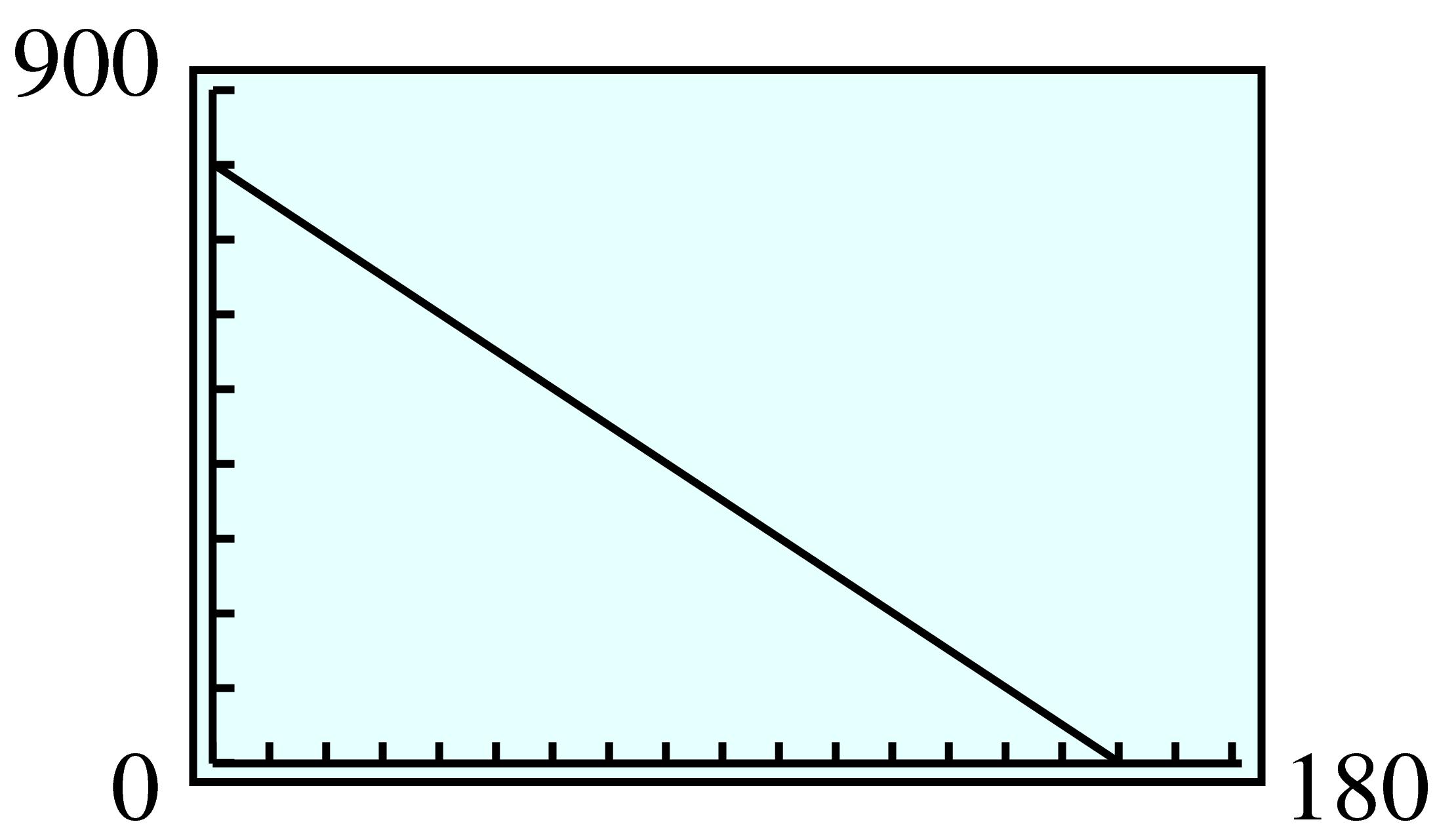
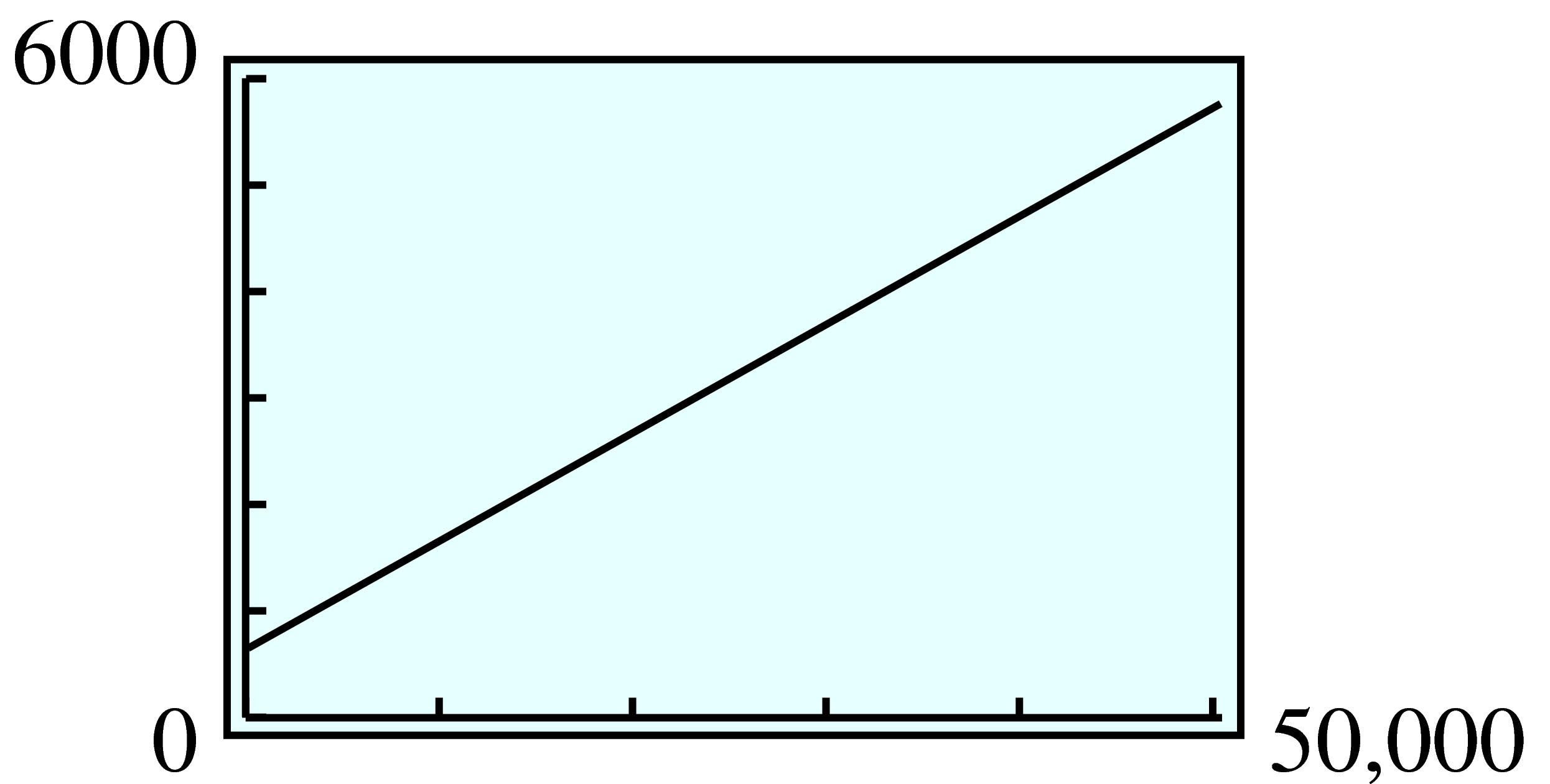
\(\displaystyle 2.40x + 3.20y = 19,200\)
The
\(y\) -intercept, 6000 gallons, is the amount of premium that the gas station owner can buy if he buys no regular. The
\(x\) -intercept, 8000 gallons, is the amount of regular he can buy if he buys no premium.
1.4 Slope 1.4.5 Problem Set 1.4
Warm Up Skills Practice 1.4.5.9. Answer .
\(\displaystyle \dfrac{3}{2} \)
\(\displaystyle 6,~ \dfrac{3}{2}\)
\(\displaystyle -9,~ \dfrac{3}{2}\)
27
1.4.5.15. Answer .
\(\displaystyle m=\dfrac{-3}{4} \)
1.4.5.17. Applications 1.4.5.21. Answer .
800
\(\displaystyle P=7000+800t\)
1.4.5.23. Answer .
The water supply is decreasing at a rate of 6 liters per day.
\(\displaystyle W=48-6t\)
1.4.5.25. Answer .
0.12 cm/kg: The spring stretches an extra 0.12 cm for each additional 1 kg mass.
1.4.5.27. Answer .
The distances to the stations are known.
5.7 km/sec
1.4.5.29.
1.5 Equations of Lines 1.5.6 Problem Set 1.5
Warm Up 1.5.6.1. Answer .
\(x\) \(-1\) \(~0~\) \(~2~\) \(~3~\) \(~4~\)
\(y\) \(10\) \(8\) \(4\) \(2\) \(0\)
The constant term is the \(y\) -intercept and the coefficient of \(x\) is the slope.
1.5.6.3. Answer .
\(\displaystyle \Delta h = 22\)
\(\displaystyle \Delta r = -57\)
Skills Practice
1.5.6.5. Answer .
\(\displaystyle y=\dfrac{-3}{2}x+\dfrac{1}{2}\)
\(\displaystyle m=\dfrac{-3}{2}; ~b=\dfrac{1}{2} \)
1.5.6.7. Answer .
\(\displaystyle y=14x-22\)
\(\displaystyle m=14; ~b=-22 \)
1.5.6.9. Answer .
\(\displaystyle y=\dfrac{-5}{3}x-6\)
\(\displaystyle x=\dfrac{-18}{5}\)
1.5.6.13. Answer .
\(\displaystyle y+5 = -3(x-2) \)
\(\displaystyle y=-3x+1\)
Applications 1.5.6.19. Answer .
\(\displaystyle M = 7000 - 400w\)
The slope tells us that Tammy’s bank account is diminishing at a rate of $400 per week, the vertical intercept that she had $7000 (when she lost all sources of income).
1.5.6.21. Answer .
\(m = -0.0018\) degree/foot, so the boiling point drops with altitude at a rate of 0.0018 degree per foot.
\(b = 212\text{,}\) so the boiling point is
\(212\degree\) at sea level (where the elevation
\(h = 0\) ).
1.5.6.23. Answer .
\(h\) \(8\) \(20\)
\(C\) \(645\) \(1425\)
\(\displaystyle C=125+65h \)
\(m =65 \text{,}\) the lesson rate is 65 dollars per hour
1.5.6.25. Answer .
\(C\) \(15\) \(-5\)
\(F\) \(59\) \(23\)
\(\displaystyle F=32+\dfrac{9}{5}C \)
\(m =\dfrac{9}{5} \text{,}\) so an increase of
\(1\degree\) C is equivalent to an increase of
\(\dfrac{9}{5}\degree\) F.
1.5.6.27. Answer .
\(m=\dfrac{-3}{820}\text{.}\) The temperature decreases 3 degrees for each increase in altitude of 820 feet.
\((19,133 \frac{1}{3}, 0)\text{.}\) At an altitude of
\(19,133 \frac{1}{3}\) feet, the temperature is
\(0\degree\) F.
\((0,70)\text{.}\) At an altitude of 0 feet, the temperature is
\(70\degree\) F.
1.5.6.29. Answer .
\(\displaystyle (0,28) \)
\(\displaystyle m=\dfrac{1}{2} \)
\(\displaystyle y= \dfrac{1}{2}x + 28 \)
\(\displaystyle 36\degree\text{C}\)
1.6 Chapter Summary and Review 1.6.3 Chapter 1 Review Problems
1.6.3.1. Answer .
\(n\) \(100\) \(500\) \(800\) \(1200\) \(1500\)
\(C\) \(4000\) \(12,000\) \(18,000\) \(26,000\) \(32,000\)
\(\displaystyle C = 20n + 2000\)
1.6.3.2. Answer .
\(t\) \(~ 5 ~\) \(~10~\) \(~15~\) \(~20~\) \(~25~\)
\(R\) \(1960\) \(1820\) \(1680\) \(1540\) \(1400\)
\(\displaystyle R = 2100 - 28t\)
\((75, 0)\text{,}\) \((0, 2100)\)
\(t\) -intercept: The oil reserves will be gone in 2080;
\(R\) -intercept: There were
\(2100\) billion barrels of oil reserves in 2005.
1.6.3.3. Answer .
\(\displaystyle 60C+100T=1200\)
\((20,0) \text{,}\) \((0,12) \)
She can spend 20 days in Atlantic City if she spends no time in Saint-Tropez, or 12 days in Saint-Tropez if she spends no time in Atlantic City.
1.6.3.4. 1.6.3.5. 1.6.3.6. 1.6.3.7. 1.6.3.8. 1.6.3.9. 1.6.3.10. Answer .
\(\displaystyle B = 800 - 5t\)
\(m = -5\) thousand barrels/minute: The amount of oil in the tanker is decreasing by 5000 barrels per minute.
1.6.3.11. Answer .
\(\displaystyle F = 500 + 0.10C\)
\(m = 0.10\text{:}\) The fee increases by $0.10 for each dollar increase in the remodeling job.
1.6.3.12. 1.6.3.13. 1.6.3.14. 1.6.3.15.
1.6.3.18. Answer .
\(d\) \(V\)
\(-5\) \(-4.8\)
\(-2\) \(-3 \)
\(1\) \(-1.2\)
\(6\) \(1.8 \)
\(10\) \(4.2\)
1.6.3.19. Answer .
\(q\) \(S\)
\(-8\) \(-8\)
\(-4\) \(36 \)
\(3\) \(168\)
\(5\) \(200 \)
\(9\) \(264\)
1.6.3.20.
1.6.3.21. Answer .
\(m=\dfrac{1}{2} \text{,}\) \(b= \dfrac{-5}{4} \)
1.6.3.22. Answer .
\(m=\dfrac{3}{4} \text{,}\) \(b= \dfrac{5}{4} \)
1.6.3.23. Answer .
\(m=-4 \text{,}\) \(b= 3 \)
1.6.3.24. Answer .
\(m=0 \text{,}\) \(b= 3 \)
1.6.3.25. Answer .
\(\displaystyle y=\dfrac{-2}{3}x +\dfrac{10}{3} \)
1.6.3.26. Answer .
\(\displaystyle y=\dfrac{3}{2}x -8 \)
1.6.3.27. Answer .
\(\displaystyle T = 62 - 0.0036h\)
\(-46\degree\text{F}\text{;}\) \(108\degree\text{F}\)
\(\displaystyle -71\degree\text{F}\)
1.6.3.28. Answer .
\(y=\dfrac{-9}{5}x+\dfrac{2}{5} \)
1.6.3.29. 1.6.3.30. Answer .
\(t\) \(0\) \(15\)
\(P\) \(4800\) \(6780\)
\(\displaystyle P = 4800 + 132t\)
\(m = 132\) people/year: the population grew at a rate of
\(132\) people per year.
1.6.3.31. Answer .
\(\displaystyle y=-2x+3\)
1.6.3.32. Answer .
\(m=\dfrac{3}{2} \text{;}\) \(b=-5\)
\(\displaystyle y=\dfrac{3}{2}x-5\)
1.6.3.33. 1.6.3.34. Answer .
\((4,0) \) and
\((0,-6) \)
\(\displaystyle \dfrac{3}{2} \)
1.6.3.35. Answer .
\(\left(\dfrac{8}{3},0 \right) \) and
\((0,-4) \)
2 Applications of Linear Models 2.1 Linear Regression 2.1.5 Problem Set 2.1
Warm Up 2.1.5.1. Answer .
a: II; b: III; c: I; d: IV
2.1.5.2. Answer .
a: III; b: IV; c: II; d: I
2.1.5.3. Answer .
\(k\) \(70\) \(50\)
\(p\) \(154\) \(110\)
\(\displaystyle p=2.2k \)
\(m =2.2 \) pounds/kg is the conversion factor from kilograms to pounds
Skills Practice 2.1.5.5. Answer .
The slope is
\(-2.5\text{,}\) which indicates that the snack bar sells 2.5 fewer cups of cocoa for each
\(1\degree\text{C}\) increase in temperature. The
\(C\) -intercept of 52 indicates that 52 cups of cocoa would be sold at a temperature of
\(0\degree\text{C}\text{.}\) The
\(T\) -intercept of 20.8 indicates that no cocoa will be sold at a temperature of
\(20.8\degree\text{C}\text{.}\)
2.1.5.9. Answer .
\(L=24+(29/7)t\text{,}\) where
\(t\) is in months
74 feet
The young whale grows in length about 4.14 foot per month
2.1.5.11. Answer .
2 min:
\(21\degree\) C; 2 hr:
\(729\degree\) C; The estimate at 2 minutes is reasonable; the estimate at 2 hours is not reasonable.
Applications 2.1.5.13. Answer .
\(\displaystyle y = 8.5 + 0.1x\)
12.7 seconds; 10.18 seconds; The prediction for the 40-year-old is reasonable, but not the prediction for the 12-year-old.
2.1.5.15. Answer .
53 sec, 64 sec
\(\displaystyle y=5.5x-8.6\)
57.95 sec
2.1.5.17. Answer .
\(\displaystyle y = 121 + 19.86t\)
2.1.5.19. Answer .
The slope tells us that the time it takes for a bird to attract a mate decreases by 0.85 days for every additional song it learns.
The
\(C\) -intercept tells us that a warbler with a repretoire of 53 songs would acquire a mate immediately. The
\(B\) -intercept tells us that a warbler with no songs would take 62 days to find a mate. These values make sense in context.
2.2 Linear Systems 2.2.5 Problem Set 2.2
Warm Up 2.2.5.1. 2.2.5.3. Skills Practice Applications 2.2.5.13. Answer .
Fitness First:
\(y=50+25x\)
\(x\) Sporthaus
Fitness First
6
560
200
12
620
350
18
680
500
24
740
650
30
800
800
36
860
950
42
920
1100
48
980
1250
2.2.5.15. Answer .
\(\displaystyle 10x + 5y = 300\)
\(\displaystyle (12,36) \)
She should buy 12 hardbacks and 36 paperbacks.
2.2.5.17. Answer .
\(\displaystyle D=120-2.5x\)
\(x=30\text{;}\) \(S=45\)
2.2.5.19. Answer .
The median age
0.3 years of age per year since 1990
See (b) above
Slightly less than 14 years since 1990
More than half the women are older than the mean age of women.
2.3 Algebraic Solution of Systems 2.3.5 Problem Set 2.3
Warm Up 2.3.5.1. Skills Practice Applications 2.3.5.11. Answer .
\(\displaystyle S=2.5x;~~D=350-4.5x\)
50 dollars per machine; 125 machines
2.3.5.13. Answer .
Pounds
% silver
Amount of silver
First alloy
\(x\) \(0.45\) \(0.45x\)
Second alloy
\(y\) \(0.60\) \(0.60y\)
Mixture
\(40\) \(0.48\) \(0.48(40)\)
\(\displaystyle 0.45x+0.60y=19.2 \)
2.3.5.15. Answer .
Rani’s speed in still water:
\(x\)
Speed of the current:
\(y\)
Rate
Time
Distance
Downstream
\(x+y\) \(45\) \(6000\)
Upstream
\(x-y\) \(45\) \(4800\)
\(\displaystyle 45(x+y)=6000 \)
\(\displaystyle 45(x-y)=4800 \)
Rani’s speed in still water is 120 meters per minute, and the speed of the current is
\(13\dfrac{1}{3} \) meters per minute.
2.3.5.17. 2.3.5.19. Answer .
Sports coupes
Wagons
Total
Hours of riveting
3
4
120
Hours of welding
4
5
155
\(\displaystyle 3x+4y=120\)
\(\displaystyle 4x+5y=155\)
20 sports coupes and 15 wagons
2.4 Gaussian Reduction 2.4.6 Problem Set 2.4
Warm Up 2.4.6.3. Answer .
Principal
Interest rate
Interest
Bonds
\(x\) \(0.10\) \(0.10x\)
Certificate
\(y\) \(0.08\) \(0.08y\)
Total
\(2000\) ——
\(184\)
\(\displaystyle x+y=2000\)
\(\displaystyle 0.10x+0.08y=184\)
Skills Practice
2.4.6.7. 2.4.6.9. 2.4.6.11. Answer .
\(\left(\dfrac{1}{2}, \dfrac{2}{3},-3 \right) \)
2.4.6.13. Answer .
\(\left(\dfrac{1}{2}, -\dfrac{1}{2},\dfrac{1}{3} \right) \)
Applications
2.4.6.17. Answer .
\(x=40\) in,
\(y=60\) in,
\(z=55\) in
2.4.6.19. Answer .
\(\dfrac{1}{2} \) lb Colombian,
\(\dfrac{1}{4} \) lb French,
\(\dfrac{1}{4} \) Sumatran
2.4.6.21.
2.5 Linear Inequalities in Two Variables 2.5.5 Problem Set 2.5
Warm Up 2.5.5.1. Answer .
\(x\) \(-2\) \(5\) \(6\) \(8\)
\(y\) \(12\) \(5\) \(4\) \(2\)
2.5.5.3. Answer .
The graph of the equation is a line, and the graph of the inequality is a half-plane. The line is the boundary of the half-plane but is not included in the solution to the inequality.
The graph of
\(x + y\ge 10,000\) includes both the line
\(x + y=10,000\) and the half-plane of the corresponding strict inequality.
Skills Practice
2.5.5.5. 2.5.5.7. 2.5.5.9. 2.5.5.11. 2.5.5.13. Applications
2.6 Chapter Summary and Review 2.6.3 Chapter 2 Review Problems
2.6.3.1. Answer .
\(\displaystyle y=0.106x + 4.6\)
\(\displaystyle 156.7\degree\text{C}\)
2.6.3.2. Answer .
\(\displaystyle y = 1.2x - 3\)
\(y = 1.197x - 3.660\text{;}\) \(68.16\) cm
2.6.3.3. 2.6.3.4.
2.6.3.7. Answer .
\(\left(\dfrac{1}{2}, \dfrac{7}{2} \right) \)
2.6.3.8. 2.6.3.9. 2.6.3.10. Answer .
\(\left(\dfrac{1}{2}, \dfrac{3}{2} \right)\)
2.6.3.11. Answer .
Consistent and independent
2.6.3.12. 2.6.3.13. 2.6.3.14. Answer .
Consistent and independent
2.6.3.15. 2.6.3.16. 2.6.3.17. 2.6.3.18. Answer .
\(\left(2,\dfrac{3}{2},-1\right) \)
2.6.3.19. 2.6.3.20.
2.6.3.21. 2.6.3.22. 2.6.3.23. Answer .
$3181.82 at 8%, $1818.18 at 13.5%
2.6.3.24. 2.6.3.25. 2.6.3.26. Answer .
20 to Boston, 25 to Chicago, 10 to Los Angeles
2.6.3.27. 2.6.3.28. 2.6.3.29. 2.6.3.30.
2.6.3.31. 2.6.3.32. 2.6.3.33. 2.6.3.34.
2.6.3.35. 2.6.3.36. 2.6.3.37. 2.6.3.38. 2.6.3.39. Answer .
\(20p+9g \le 120\text{,}\) \(10p+10g \le 120\text{,}\) \(p\ge 0\text{,}\) \(g\ge 0\)
2.6.3.40. Answer .
\(x+y \le 32\text{,}\) \(2x+1.6y \ge 56\text{,}\) \(x\ge 0\text{,}\) \(y\ge 0\text{,}\) where
\(x\) represents ounces of tofu,
\(y\) the ounces of tempeh
3 Quadratic Models 3.1 Extraction of Roots 3.1.9 Problem Set 3.1
Warm Up 3.1.9.1. 3.1.9.3. Answer .
\(\displaystyle \sqrt{6}\)
3.1.9.4. Answer .
\(\displaystyle \pm \dfrac{5}{2}\)
\(\displaystyle \pm \sqrt{5}\)
3.1.9.5. Answer .
Two solutions. \(\approx \pm 2.5\)
\(\displaystyle \pm \sqrt{6}\)
Skills Practice
3.1.9.7. 3.1.9.9. Answer .
\(\dfrac{5}{2},~\dfrac{-3}{2} \)
3.1.9.11. Answer .
\(\dfrac{2}{3} \pm \dfrac{\sqrt{5}}{3}\)
3.1.9.13. Answer .
\(\dfrac{7}{8},\pm \dfrac{\sqrt{8}}{8} \)
3.1.9.19. 3.1.9.21. Answer .
\(\pm pi \sqrt{\dfrac{L}{8}}\)
Applications 3.1.9.25. Answer .
\(\displaystyle A=1600(1+r)^2\)
\(~r~\) \(0.02\) \(0.04\) \(0.06\) \(0.08\)
\(~A~\) \(1664.64\) \(1730.56\) \(1797.76\) \(1866.24\)
11.8%
3.1.9.27. 3.1.9.29. Answer .
\(\displaystyle V=62.8r^2\)
\(\displaystyle \dfrac{1}{4}\)
1.96 cm
3.1.9.31. Answer .
\(\displaystyle \pm \sqrt{\dfrac{bc}{a}}\)
\(\displaystyle \pm \sqrt{\dfrac{ac}{b}}\)
3.2 Intercepts, Solutions, and Factors 3.2.6 Problem Set 3.2
Warm Up
3.2.6.1. Answer .
\(\displaystyle 2b^2+9b-18\)
\(\displaystyle 12z^2-35z+8\)
3.2.6.3. Answer .
\(\displaystyle 6p^3-33p^2+45p\)
\(\displaystyle 6v^3+16v^2-32v\)
3.2.6.5. Answer .
\(\displaystyle (x-4)(x+4)\)
\(\displaystyle x(x-16)\)
\(\displaystyle (x-4)(x-4)\)
3.2.6.7. 3.2.6.9. 3.2.6.11. Skills Practice
3.2.6.13. 3.2.6.15. 3.2.6.17. 3.2.6.19.
3.2.6.21. Answer .
\(\dfrac{7}{8} \pm \dfrac{\sqrt{8}}{8}\)
3.2.6.23. 3.2.6.27. Answer .
All three graphs have the same
\(x\) -intercepts.
Applications 3.2.6.29. Answer .
c. 306.5 ft at 0.625 sec d. 1.25 sec e. 5 sec
3.2.6.31. Answer .
b.
\(h^2+10^2=(h+2)^2\) c. 24 ft
3.2.6.33. Answer .
\(\displaystyle l=x-4,~w=x-4,~h=2,~V=2(x-4)^2\)
0 cubic in, 2 cubic in, 8 cubic in, etc.
\(\displaystyle x = 4\)
9 in by 9 in
\(\displaystyle 2(x-4)^2 = 50;~ x=9\)
3.2.6.34. Answer .
a.
\(l=6, ~w=1-2x, ~h=x, ~V=6x(1-2x)~~\) e.
\(6x(1-2x)=\dfrac{3}{4};~~\dfrac{1}{4}~\) ft
3.3 Graphing Parabolas 3.3.6 Problem Set 3.3
Warm Up 3.3.6.4. Answer .
factoring; \(0,10\)
extraction of roots; \(\pm \sqrt{10}\)
factoring; \(\dfrac{-1}{2}, 1\)
extraction of roots; \(\dfrac{-5}{2}, \dfrac{-5}{2}\)
Skills Practice 3.3.6.9.
3.3.6.13. 3.3.6.15. Answer .
\((0,0), (-2,0); (-1,-3)\)
3.3.6.17. Answer .
\((0,0), (20,0); (10,200)\)
Applications 3.3.6.19. Answer .
\(\displaystyle (2000, 400)\)
\(\displaystyle (0,0), (4000,0)\)
\(\displaystyle x \gt 4000\)
3.3.6.21. Answer .
basic parabola
narrower
wider
narrower and reflected about \(y\) -axis
3.3.6.23. Answer .
\(x\) -intercepts at 0 and 4
\(x\) -intercepts at 0 and \(-4\)
reflection of (a) about \(y\) -axis
reflection of (b) about \(y\) -axis
3.4 Completing the Square 3.4.4 Problem Set 3.4
Warm Up 3.4.4.3. Answer .
\(\displaystyle x^2+10x+25\)
\(\displaystyle x^2-12x+36\)
\(\displaystyle x^2-24x+144\)
\(\displaystyle x^2+30x+225\)
Skills Practice
3.4.4.7. 3.4.4.9. Answer .
\(-1 \pm \sqrt{\dfrac{5}{2}}\)
3.4.4.11. Answer .
\(\dfrac{-5}{2} \pm \sqrt{\dfrac{45}{4}}\)
Applications
3.4.4.17. Answer .
\(\displaystyle (\dfrac{1}{4} \pm \sqrt{\dfrac{13}{15}}, 0)\)
\(\displaystyle (\dfrac{1}{4}, -3\dfrac{1}{4})\)
3.4.4.19. Answer .
\(\displaystyle (-2,0),~(\dfrac{2}{5},0)\)
\(\displaystyle (\dfrac{-4}{5}, -7\dfrac{1}{5})\)
3.4.4.21. Answer .
\(\displaystyle L^2+(L-4)^2=20^2\)
12 in by 16 in
3.4.4.23. Answer .
\(\displaystyle A = \dfrac{1}{2}(x^2-y^2)\)
\(\displaystyle A = \dfrac{1}{2}(x-y)(x+y)\)
18 sq ft
3.4.4.25. Answer .
\(\displaystyle A = (x+y)^2\)
\(\displaystyle A = x^2+2xy+y^2\)
3.4.4.27. 3.4.4.29. Answer .
\(\dfrac{b}{2} \pm \dfrac{b^2-4c}{4}\)
3.4.4.31. Answer .
\(\pm \sqrt{\dfrac{V}{2w} - s^2}\)
3.4.4.33. Answer .
\((-15,0), (15,0); (0,255)\)
3.4.4.35.
3.5 Chapter 3 Summary and Review 3.5.3 Chapter 3 Review Problems
3.5.3.1. 3.5.3.2. 3.5.3.3. 3.5.3.4. Answer .
\(\dfrac{1 \pm \sqrt{15}}{7}\)
3.5.3.5. 3.5.3.6.
3.5.3.7. 3.5.3.8. 3.5.3.9. 3.5.3.10.
3.5.3.15. Answer .
Vertex:
\((0,0)\text{,}\) \(y\) -int:
\((0,0)\text{,}\) \(x\) -int:
\((0,0)\)
3.5.3.17. Answer .
Vertex:
\(\left(\dfrac{9}{2},\dfrac{-81}{4}\right)\text{,}\) \(y\) -int:
\((0,0)\text{,}\) \(x\) -int:
\((0,0),~(9,0)\)
3.5.3.19. 3.5.3.20. Answer .
\(\dfrac{-3}{2} \pm \sqrt{\dfrac{21}{4}}\)
3.5.3.21. Answer .
\(\dfrac{3}{2} \pm \sqrt{\dfrac{3}{4}}\)
3.5.3.22. Answer .
\(\dfrac{1}{3} \pm \sqrt{\dfrac{10}{9}}\)
3.5.3.23. Answer .
\(v=\pm \sqrt{\dfrac{2K}{m}}\)
3.5.3.24. 3.5.3.25. Answer .
\(s=\pm \sqrt{\dfrac{3V}{h}}\)
3.5.3.26. Answer .
\(r=\pm \sqrt{\dfrac{A}{P}}-1\)
3.5.3.27. 3.5.3.28. 3.5.3.29. 3.5.3.30. 3.5.3.31. Answer .
\(\sqrt{108} \approx 10.4\) in
3.5.3.32. 3.5.3.33. 3.5.3.34.
3.5.3.35. Answer .
\(A_1=x^2-\left(\dfrac{1}{2}y^2+\dfrac{1}{2}y^2\right)=x^2-y^2;~~A_2=(x+y)(x-y)=x^2-y^2\)
3.5.3.36. Answer .
\(A_1=\pi (x+y)^2- \pi x^2 - \pi y^2 = 2 \pi xy;~~A_2=\pi y (2x) = 2 \pi xy\)
4 Applications of Quadratic Models 4.1 Quadratic Formula 4.1.6 Problem Set 4.1
Warm Up 4.1.6.1. Answer .
\(\displaystyle 8-2\sqrt{20}\)
\(\displaystyle 9\)
4.1.6.3. Answer .
\(\displaystyle A=lw,~P=2l+2w\)
\(A=24\) sq ft, \(P=20\) ft
\(A=24\) sq ft, \(P=22\) ft
Skills Practice
4.1.6.5. 4.1.6.7. 4.1.6.9. 4.1.6.11. Answer .
Approximately \((1.5,0)\) and \((-0.3,0)\)
\(\dfrac{3}{2}\) and \(\dfrac{-1}{3}\text{.}\) These are the \(x\) -intercepts of the graph.
4.1.6.13. Answer .
\((5,0)\) and \((1,0)\text{;}\) \((3,0)\text{;}\) no \(x\) -intercepts
1 and 5; 3; \(\dfrac{6 \pm i\sqrt{12}}{2}\text{.}\) The real-valued solutions are the \(x\) -intercepts of the graph. If the solutions are complex, the graph has no \(x\) -intercepts.
4.1.6.15. Answer .
\(\displaystyle x^2-4x-1=0\)
\(\displaystyle x^2-8x+25=0\)
4.1.6.17. Answer .
\(\dfrac{-4 \pm \sqrt{16-64h}}{32}\)
4.1.6.19. Answer .
\(\dfrac{v \pm \sqrt{v^2-2as}}{a}\)
4.1.6.21. Answer .
\(\dfrac{-1 \pm \sqrt{1+8S}}{2}\)
Applications 4.1.6.23. 4.1.6.25. 4.1.6.27. Answer .
b.
\(10h(2h-6)=2160~~~\) c. 12 ft by 18 ft by 10ft
4.2 The Vertex 4.2.5 Problem Set 4.2
Warm Up 4.2.5.1. Answer .
\(t\) \(0\) \(0.25\) \(0.5\) \(0.75\) \(1\) \(0.25\) \(1.5\)
\(h\) \(-12\) \(-5\) \(0\) \(3\) \(4\) \(3\) \(0\)
\(\displaystyle (1,4)\)
The wrench reaches its greatest height of 4 feet.
The wrench reaches its greatest height 1 second after Francine throws it.
4.2.5.3. Answer .
\(\displaystyle y = x^2-3x-4\)
y = -x^2+3x+4
Skills Practice 4.2.5.7. Answer .
\(\displaystyle (3,0)\)
\(\displaystyle (3,0)\)
\(\displaystyle (3,4)\)
4.2.5.9. Answer .
\(\displaystyle (3,4)\)
\(\displaystyle y=2x^2-12x+22\)
4.2.5.11. Answer .
\(\displaystyle y=a(x+2)^2+6\)
3
Applications 4.2.5.17. Answer .
\(\displaystyle l=40-w;~A=40w-w^2\)
400 sq yd; 20 yd by 20 yd
4.2.5.19. Answer .
(table)
\(\displaystyle 20+2x,~ 60-3x,~ (20+2x)(60-3x)\)
(table)
\(\displaystyle x= 20\)
$24, $36
$1350, $30, 45 rooms
4.2.5.21. Answer .
\(\displaystyle h=\dfrac{-1}{40}(x-80)^2+164\)
160.99 ft
4.2.5.23. 4.2.5.25. Answer .
\(\displaystyle (-4,0),~(0,2)\)
\(~~~~\) \(x \lt -4\) \(-4 \lt x \lt 2\) \(x \gt 2\)
\(Y_1\) \(-\) \(+\) \(+\)
\(Y_2\) \(-\) \(-\) \(+\)
\(Y_3\) \(+\) \(-\) \(+\)
4.3 Curve Fitting 4.3.5 Problem Set 4.3
Warm Up 4.3.5.1. Answer .
\((4,10),~(0,-22),~(4 \pm \sqrt{5},0)\)
4.3.5.3. Answer .
\(\displaystyle 25-2x\)
\(\displaystyle 30+4x\)
Skills Practice 4.3.5.13. Applications 4.3.5.15. Answer .
\(\displaystyle y=a(x-5)^2-10=-0.2x^2+11x-78\)
\(\displaystyle 42\)
4.3.5.17. Answer .
\(D=\dfrac{1}{2}n^2 - \dfrac{3}{2}n\)
4.3.5.19. Answer .
\(\displaystyle N=-0.59t^2+7.33t-2.54\)
\(\displaystyle 2000;~7\)
4.3.5.21. Answer .
\(\displaystyle (0,0.14)\)
\(\displaystyle y=-1.786x^2+0.14\)
4.4 Quadratic Inequalities 4.4.6 Problem Set 4.4
Warm Up
4.4.6.1. Answer .
\(\displaystyle (-4,0),~(6,0)\)
up
4.4.6.3. Answer .
\(\displaystyle (3 \pm \sqrt{12},0)\)
down
4.4.6.5. Answer .
\(\displaystyle [0,4)\)
\(\displaystyle (5,8)\)
Skills Practice 4.4.6.7. Answer .
See graph.
\(x \gt 3\) or
\(x \lt -1\)
4.4.6.9. Answer .
\(\displaystyle -12, 5\)
\(x \lt -12\) or \(x \gt 15\)
4.4.6.11. Answer .
\(\displaystyle (-\infty,-3) \cup (6, \infty)\)
\(\displaystyle (-3,6)\)
\(\displaystyle [-2,5]\)
\(\displaystyle (-\infty,2] \cup [5,\infty)\)
4.4.6.13. Answer .
\(x \lt -2\) or
\(x \gt 3\)
4.4.6.15.
4.4.6.17. 4.4.6.19. Answer .
\((-\infty, \dfrac{-1}{2}) \cup (4, \infty)\)
4.4.6.21. Answer .
\((-\infty, -2.24) \cup (2.24, \infty)\)
4.4.6.23. Applications 4.4.6.27. Answer .
\((-\infty, -4.2) \cup (2.6, \infty)\)
4.4.6.33. Answer .
\(\displaystyle 60-x;~~12+\dfrac{1}{2}x\)
\(\displaystyle y=(60-x)(12+\dfrac{1}{2}x)\)
882 bu; 18 trees
Between 10 and 26, inclusive
4.5 Chapter 4 Summary and Review 4.5.3 Chapter 4 Review Problems
4.5.3.1. 4.5.3.2. Answer .
\(\dfrac{3 \pm \sqrt{5}}{2}\)
4.5.3.3. Answer .
\(-\dfrac{4 \pm \sqrt{8}}{2}\)
4.5.3.4. Answer .
\(\dfrac{-2 \pm \sqrt{28}}{4}\)
4.5.3.5. Answer .
\(\dfrac{6 \pm \sqrt{36-12h}}{6}\)
4.5.3.6. Answer .
\(\dfrac{3 \pm \sqrt{9+8D}}{2}\)
4.5.3.7. Answer .
one repeated real solution
4.5.3.8. 4.5.3.9. 4.5.3.10. Answer .
two distinct real soutions
4.5.3.11. Answer .
\(\displaystyle h=100t-2.8t^2\)
(graph)
893 ft
\(15 \dfrac{5}{7}\) sec and 20 sec
4.5.3.12. Answer .
1.5 sec, 11.025 m
7.056 m
0.6 sec
0.5 sec, 2.5 sec
\((0,0),~(3,0).\) She leaves the springboard at \(t=0\) seconds and returns to the springboard at \(t=3\) seconds.
4.5.3.13. Answer .
\(\left(\dfrac{1}{2}, \dfrac{-49}{4}\right)\text{,}\) \((-3,0)\text{,}\) \((4,0)\text{,}\) \((0,-12)\)
4.5.3.14. Answer .
\(\left(\dfrac{1}{4}, \dfrac{-31}{8}\right)\text{,}\) no \(x\) -intercepts,\(~(0,-4)\)
4.5.3.15. Answer .
\(\displaystyle (1,5),~(-1.24,0),~(3.24,0),~(0,4)\)
4.5.3.16. Answer .
\(\left(\dfrac{3}{2}, \dfrac{7}{4}\right),~\) no \(x\) -intercepts,\(~(0,4)\)
4.5.3.17. 4.5.3.18. Answer .
\(\displaystyle (1,5)\)
\(\displaystyle y=2x^2+4x+7\)
4.5.3.19. 4.5.3.20. Answer .
\(\displaystyle R=1200x-80x^2\)
$7.50
$4500
4.5.3.21. Answer .
\(\displaystyle y=60(4+2x)(32-4x)\)
2
4.5.3.22. Answer .
\(\displaystyle R=(20+x)(500-10x)\)
$35
4.5.3.23. 4.5.3.24. Answer .
\(y=-\dfrac{1}{2}x^2-4x+10\)
4.5.3.25. Answer .
\(\displaystyle h=36.98t+5.17\)
116.1 m, 153.1 m
(graph)
\(\displaystyle h=-4.858t^2+47.67t+0.89\)
100.2 m, 113.9 m
(graph)
quadratic
4.5.3.26. Answer .
\(\displaystyle y=-0.05x^2-0.003x+234.2\)
\((-0.03, 234.2)~\) The velocity of the debris at its maximum height of 234.2 feet. The velocity there is actually zero.
4.5.3.27. Answer .
\((-\infty,-2) \cup (3,\infty)\)
4.5.3.28. 4.5.3.29. 4.5.3.30. Answer .
\((-\infty,-\dfrac{1}{3}) \cup (2,\infty)\)
4.5.3.31. 4.5.3.32. Answer .
\((-\infty,-\sqrt{3}) \cup (\sqrt{3},\infty)\)
4.5.3.33. Answer .
\(\displaystyle R=p(220-\dfrac{1}{4}p)\)
\(\displaystyle 400 \lt p \lt 480\)
4.5.3.34. Answer .
\(\displaystyle R=p(30-\dfrac{1}{2}p)\)
\(\displaystyle 20 \lt p \lt 40\)
5 Functions and Their Graphs 5.1 Functions 5.1.7 Problem Set 5.1
Warm Up Skills Practice 5.1.7.9. Answer .
input: \(v\text{,}\) output: \(x\)
15
\(-1, \dfrac{5}{2}\text{.}\)
5.1.7.11. Answer .
\(\displaystyle \dfrac{-1}{3}\)
\(\displaystyle \dfrac{-4}{9}\)
\(\displaystyle \dfrac{-3}{4}\)
\(\displaystyle -0.530\)
Applications 5.1.7.13. 5.1.7.15.
5.1.7.17. 5.1.7.19. Answer .
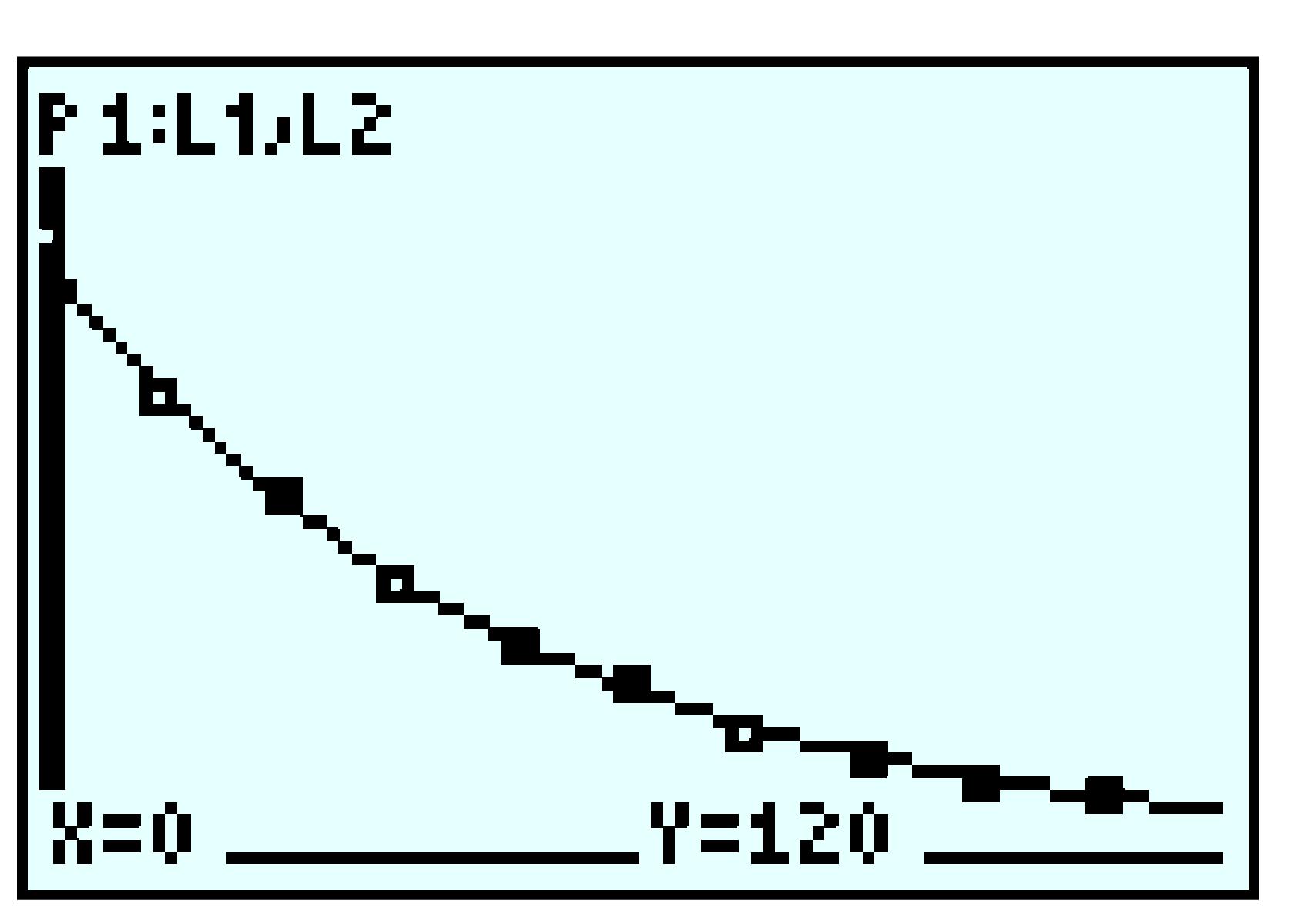
\(\displaystyle f(12) \approx 1920;~~ f(5)=1500,~f(15)=1500\)
\(\displaystyle 7\lt d\lt 13\)
5.1.7.21. Answer .
\(\displaystyle F(1992) = 7.5\%\)
\(\displaystyle F(2000) = 4\%\)
\(\displaystyle F(1998+ = 4.5\%,~ F(2001) = 4.5\%\)
5.1.7.25. Answer .
\(N(6000) = 2000\text{:}\) 2000 cars will be sold at a price of $6000.
decrease
30,000. At a price of $30,000, they will sell 400 cars.
5.2 Graphs of Functions 5.2.6 Problem Set 5.2
Warm Up 5.2.6.5. Answer .
\(\displaystyle x \gt 0.6\)
\(\displaystyle x \lt -0.4\)
Skills Practice Applications
5.2.6.11. Answer .
\(\displaystyle -2, 0, 5\)
2
\(\displaystyle h(-2)=0,~h(1)=0,~h(0)=-2\)
5
3
increasing: \((-4,-2)\) and \((0,3)\text{;}\) decreasing: \((-2,0)\)
5.2.6.13. Answer .
\(\displaystyle 0, ~\dfrac{1}{2}, ~0\)
\(\displaystyle \dfrac{5}{6}\)
\(\displaystyle \dfrac{-5}{6},~\dfrac{-1}{6},~\dfrac{7}{6},~\dfrac{11}{6}\)
\(\displaystyle 1,~-1\)
Max at \(x=-1.5,~0.5\text{,}\) min at \(x=-0.5,~1.5\)
5.2.6.15. Answer .
\(f(1000) = 1495\text{:}\) The speed of sound at a depth of
\(1000\) meters is approximately
\(1495\) meters per second.
\(d = 570\) or
\(d = 1070\text{:}\) The speed of sound is
\(1500\) meters per second at both a depth of
\(570\) meters and a depth of
\(1070\) meters.
The slowest speed occurs at a depth of about
\(810\) meters and the speed is about
\(1487\) meters per second, so
\(f(810) = 1487\text{.}\)
\(f\) increases from about
\(1533\) to
\(1541\) in the first
\(110\) meters of depth, then drops to about
\(1487\) at
\(810\) meters, then rises again, passing
\(1553\) at a depth of about
\(1600\) meters.
5.2.6.17. 5.2.6.19. Answer .
\(\displaystyle -1, 1\)
\(\displaystyle (-1,1)\)
\(\displaystyle [-3,-2] \cup [2,3]\)
\(\displaystyle [-5,5]\)
5.2.6.21. Answer .
\(\displaystyle -2,~2\)
\(\displaystyle -2.8,~0,~2.8\)
\(-2.5 \lt q \lt -1.25\) and \(1.25 \lt q \lt 2.5\)
\(-2 \lt q \lt 0\) and \(2 \lt q\)
5.2.6.23. Answer .
\(\displaystyle g(-6)=0,~g(6)=0,~g(0)=6\)
none
\(g(x)\) is undefined for those
\(x\) -values
5.2.6.25. Answer .
\(\displaystyle 0,~5\)
\(\displaystyle 0,~\dfrac{-3}{2}\)
\(\displaystyle \dfrac{5}{6}\)
\(\displaystyle -5,~\dfrac{1}{2}\)
5.3 Some Basic Graphs 5.3.4 Problem Set 5.3
Warm Up 5.3.4.1. Answer .
\(\displaystyle 4\)
\(\displaystyle 2\)
5.3.4.3. Answer .
\(\displaystyle 2.080\)
\(\displaystyle 6.366\)
\(\displaystyle -0.126\)
\(\displaystyle -1.458\)
5.3.4.5. Answer .
\(\displaystyle \dfrac{1}{2}\)
\(\displaystyle \dfrac{-1}{3}\)
5.3.4.7. 5.3.4.9. Answer .
\(\displaystyle -50 \)
\(\displaystyle -43\)
\(\displaystyle 144\)
Skills Practice
5.3.4.11. 5.3.4.13. 5.3.4.15. 5.3.4.17. Answer .
\(\displaystyle f\)
\(\displaystyle g\)
Applications 5.3.4.19. Answer .
\((-\infty,0) \cup [0.5,\infty) \)
5.3.4.21. Answer .
(b): 2 units down, (c): 1 unit up
5.3.4.23. Answer .
(b): 1.5 units left, (c): 1 unit right
5.3.4.25. Answer .
(b): reflected about
\(x\) -axis, (c): reflected about
\(y\) -axis
5.3.4.27. 5.3.4.29. Answer .
horizontal shift of square root
\(y=\sqrt{x}\)
vertical shift of cube root
\(y=\sqrt[3]{x}\)
vertical shift of absolute value
\(y=\abs{x}\)
vertical flip of reciprocal
\(y=\dfrac{1}{x}\)
vertical flip and vertical shift of cube
\(y=x^3\)
vertical flip and vertical shift of inverse-square
\(y=\dfrac{1}{x^2} \)
5.3.4.31. Answer .
\(\displaystyle x \lt 2\)
\(\displaystyle x \gt \dfrac{-2}{3}\)
5.3.4.33. Answer .
no solution
\(\displaystyle 29\lt x\le 61\)
5.4 Direct Variation 5.4.6 Problem Set 5.4
Warm Up 5.4.6.1. Answer .
\(\displaystyle -10\)
\(\displaystyle -16, 20\)
Skills Practice 5.4.6.3. Answer .
\(\displaystyle y=0.3x\)
\(x\) \(2\) \(5\) \(8\) \(12\) \(15\)
\(y\) \(-0.6\) \(1.5\) \(2.4\) \(3.6\) \(4.5\)
\(y\) doubles also
Applications 5.4.6.9. Answer .
\(\text{Price of item} \) \(18\) \(28\) \(12\)
\(\text{Tax} \) \(1.17\) \(1.82\) \(0.78\)
\(\text{Tax}/\text{Price} \) \(\alert{0.065}\) \(\alert{0.065}\) \(\alert{0.065}\)
\(\displaystyle T = 0.065p\)
5.4.6.11. Answer .
\(\displaystyle m = 0.165w\)
\(w\) \(50\) \(100\) \(200\) \(400\)
\(m\) \(\alert{8.25}\) \(\alert{16.5}\) \(\alert{33}\) \(\alert{66}\)
5.4.6.13. Answer .
\(\displaystyle v=15.306 d\)
3985 million light-years
18,979 km/sec
5.4.6.15. Answer .
\(\displaystyle P = \dfrac{1825}{8192}w^3\approx0.228w^3\)
\(w\) \(10\) \(20\) \(40\) \(80\)
\(P\) \(\alert{223} \) \(\alert{1782} \) \(\alert{14,259} \) \(\alert{114,074} \)
5.4.6.17. Answer .
\(\displaystyle d = 0.005v^2\)
5.4.6.19. Answer .
\(\displaystyle W = 600d^2 \)
5.4.6.20. Answer .
Wind resistance quadruples.
It is one-ninth as great.
It is decreased by 19% because it is 81% of the original.
5.5 Inverse Variation 5.5.4 Problem Set 5.5
Warm Up
5.5.4.1. Answer .
\(R=\dfrac{1}{3}I\text{.}\) Not inverse variation.
5.5.4.3. Answer .
\(W=32,000-d\) Not inverse variation.
Skills Practice 5.5.4.5. 5.5.4.7. Answer .
\(\displaystyle y=\dfrac{120}{x}\)
\(x\) \(4\) \(8\) \(20\) \(30\) \(40\)
\(y\) \(30\) \(15\) \(6\) \(4\) \(3\)
\(y\) is divided by 2
Applications 5.5.4.13. Answer .
\(\text{Width (feet)} \) \(2\) \(2.5\) \(3\)
\(\text{Length (feet)} \) \(12\) \(9.6\) \(8\)
\(\text{Length}\times \text{width} \) \(\alert{24}\) \(\alert{24}\) \(\alert{24}\)
\(\displaystyle L = \dfrac{24}{w} \)
5.5.4.15. Answer .
\(\displaystyle B = \dfrac{88}{d}\)
\(d\) \(1\) \(2\) \(12\) \(24\)
\(B\) \(\alert{88} \) \(\alert{44} \) \(\alert{7.3} \) \(\alert{3.7} \)
It is one half as strong.
5.5.4.17. Answer .
645
\(\displaystyle D=\dfrac{64,500}{n}\)
215
5.5.4.18. Answer .
\(\displaystyle m =\dfrac{8}{p} \)
5.5.4.20. Answer .
\(\displaystyle T=\dfrac{4000}{d} \)
5.5.4.22. Answer .
It is one-fourth the original illumination.
It is one-ninth the illumination.
It is 64% of the illumination.
5.6 Functions as Models 5.6.6 Problem Set 5.6
Warm Up
5.6.6.1. Answer .
\(\displaystyle (0, \infty)\)
none
\(\displaystyle (-infty, 0)\)
none
5.6.6.3. Answer .
none
\(\displaystyle (0, \infty)\)
none
none
5.6.6.5. Answer .
\(\displaystyle (-infty, 0)\)
none
\(\displaystyle (0, \infty)\)
none
5.6.6.7. Answer .
\(\displaystyle s=h(t)\)
After 3 seconds, the duck is at a height of 7 meters.
Skills Practice Applications
5.6.6.21. Answer .
\(y = x^3\) stretched or compressed vertically
5.6.6.23. Answer .
\(y =\dfrac{1}{x} \) stretched or compressed vertically
5.6.6.25. 5.6.6.27. 5.6.6.29. Absolute Value
5.6.6.1. Answer .
\(\displaystyle \abs{x}=6 \)
5.6.6.3. Answer .
\(\displaystyle \abs{p+3}=5 \)
5.6.6.5. Answer .
\(\displaystyle \abs{t-6}\lt 3 \)
5.6.6.7. Answer .
\(\displaystyle \abs{b+1}\ge 0.5 \)
5.6.6.9. Answer .
\(\displaystyle -7\le x\le 1\)
\(x\lt -8\) or
\(x\gt 2\)
5.6.6.11.
5.6.6.13. Answer .
\(x=\dfrac{-3}{2} \) or
\(x=\dfrac{5}{2} \)
5.6.6.15. 5.6.6.17. 5.6.6.19. Answer .
\(w=\dfrac{13}{2} \) or
\(w=\dfrac{15}{2} \)
5.6.6.21. 5.6.6.23.
5.6.6.25. Answer .
\(\dfrac{-9}{2}\lt x \lt \dfrac{-3}{2} \)
5.6.6.27. Answer .
\(d\le -2~ \) or
\(~ d\ge 5 \)
5.6.6.29. 5.6.6.31. 5.6.6.33. Answer .
\(T\le 3.2~\) or
\(~T\ge 3.3 \)
5.6.6.35.
5.7 Chapter 5 Summary and Review 5.7.3 Chapter 5 Review Problems
5.7.3.1. Answer .
A function: Each
\(x\) has exactly one associated
\(y\) -value.
5.7.3.2. 5.7.3.3. Answer .
Not a function: The IQ of
\(98\) has two possible SAT scores.
5.7.3.4. 5.7.3.5. Answer .
\(N(10) = 7000\text{:}\) Ten days after the new well is opened, the company has pumped a total of
\(7000\) barrels of oil.
5.7.3.6. Answer .
\(H(16) = 3\text{:}\) At 16 mph, the trip takes 3 hours.
5.7.3.7. Answer .
\(F(0) = 1, ~~F(-3) =\sqrt{37}\)
5.7.3.8. Answer .
\(G(0) = -2, ~~G(20) =\sqrt[3]{12}\)
5.7.3.9. Answer .
\(h(8) = -6, ~~h(-8) = -14\)
5.7.3.10. Answer .
\(m(5) = 6, ~~m(-40) =-4.8\)
5.7.3.11. Answer .
\(\displaystyle P(0)=5\)
x=5,~x=1
5.7.3.12. Answer .
R(0)=2
\(\displaystyle x=2,~x=-2\)
5.7.3.13. Answer .
\(\displaystyle f (-2) = 3, ~~f (2) = 5\)
\(\displaystyle t = 1, ~~t = 3\)
\(t\) -intercepts
\((-3, 0), (4, 0)\text{;}\) \(f (t)\) -intercept:
\((0, 2)\)
Maximum value of
\(5\) occurs at
\(t = 2\)
5.7.3.14. Answer .
\(\displaystyle P(-3)=-2, ~~P(3)=3\)
\(\displaystyle z = -5,~ \dfrac{-1}{2},~4\)
\((-4, 0), (-1, 0), (5,0)\text{;}\) \((0, 3)\)
Maximum value of
\(-3\) occurs at
\(z = -2\)
5.7.3.15. 5.7.3.16. 5.7.3.17. 5.7.3.18.
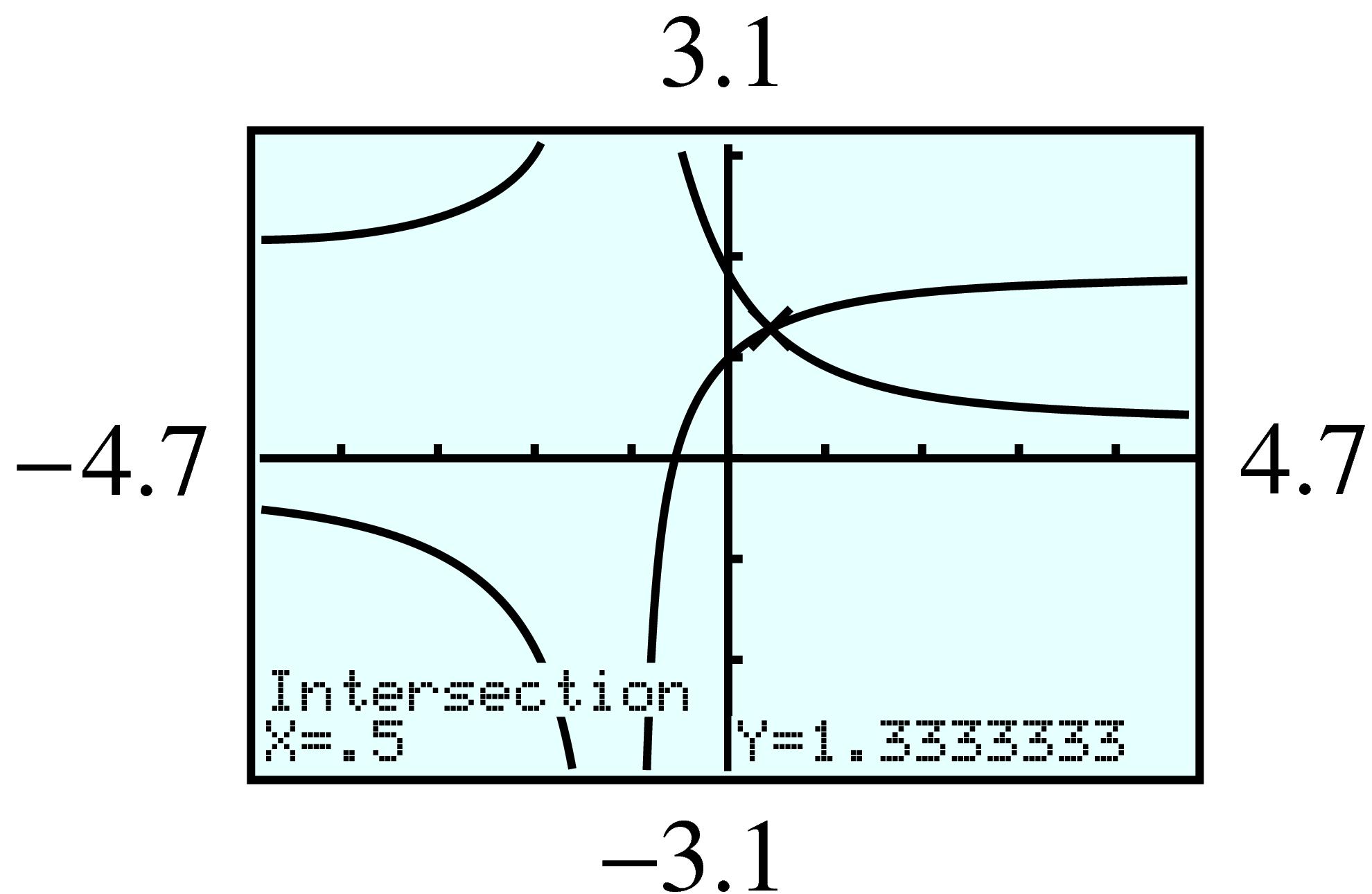
5.7.3.23. Answer .
\(\displaystyle x = \dfrac{1}{2}= 0.5\)
\(\displaystyle x = \dfrac{27}{8}\approx 3.4\)
\(\displaystyle x \gt 4.9\)
\(\displaystyle x \le 2.0\)
5.7.3.24. Answer .
\(\displaystyle x = 0.4\)
\(\displaystyle x = 3.2\)
\(\displaystyle 0 \lt x \le 4.5\)
\(x \lt 0\) or
\(x \gt 0.2\)
5.7.3.25. Answer .
\(\displaystyle x\approx\pm 5.8 \)
\(\displaystyle x = \pm 0.4\)
\(-2.5\lt x \lt 0\) or
\(0\lt x\lt 2.5\)
\(x \le -0.5\) or
\(x\ge 0.5\)
5.7.3.26. Answer .
\(\displaystyle x = 0.5\)
\(\displaystyle x = 2.9\)
\(\displaystyle 0 \le x \lt 2.3\)
\(\displaystyle x \ge 1.7\)
5.7.3.27. 5.7.3.28. 5.7.3.29. 5.7.3.30. 5.7.3.31. Answer .
\(\displaystyle d = 1.75t^2\)
5.7.3.32. Answer .
\(\displaystyle V=\dfrac{4T}{P}\)
5.7.3.33. 5.7.3.34. 5.7.3.35. Answer .
\(\displaystyle w = \dfrac{k}{r^2}\)
\(3960\sqrt{3}\approx 6860\) miles
5.7.3.43. Answer .
\(\displaystyle g(x)=\dfrac{24}{x} \)
5.7.3.44. Answer .
\(\displaystyle F(x)=-x^3 \)
5.7.3.45. Answer .
\(x\) \(0\) \(4\) \(8\) \(14\) \(16\) \(22\)
\(y\) \(24\) \(20\) \(16\) \(10\) \(8\) \(2\)
\(\displaystyle y = 24 - x\)
5.7.3.46. Answer .
\(x\) \(0\) \(4\) \(10\) \(12\) \(14\) \(16\)
\(y\) \(0\) \(6\) \(15\) \(18\) \(21\) \(24\)
\(\displaystyle y = \dfrac{3}{2}x\)
5.7.3.47. Answer .
\(x\) \(0\) \(1\) \(4\) \(9\) \(16\) \(25\)
\(y\) \(0\) \(1\) \(2\) \(3\) \(4\) \(5\)
\(\displaystyle y = \sqrt{x} \)
5.7.3.48. Answer .
\(x\) \(0.25\) \(0.50\) \(1.00\) \(1.50\) \(2.00\) \(4.00\)
\(y\) \(4.00\) \(2.00\) \(1.00\) \(0.67\) \(0.50\) \(0.25\)
\(\displaystyle y = \dfrac{1}{x}\)
5.7.3.49. Answer .
\(x\) \(-3\) \(-2\) \(-1\) \(0\) \(1\) \(2\)
\(y\) \(5\) \(0\) \(-3\) \(-4\) \(-3\) \(0\)
\(\displaystyle y = x^2-4 \)
5.7.3.50. Answer .
\(x\) \(-3\) \(-2\) \(-1\) \(0\) \(1\) \(4\)
\(y\) \(0\) \(5\) \(8\) \(9\) \(8\) \(-7\)
\(\displaystyle y = 9 - x^2\)
6 Powers and Roots 6.1 Integer Exponents 6.1.5 Problem Set 6.1
Warm Up 6.1.5.1. Answer .
\(\displaystyle -2z^2\)
\(\displaystyle -24z^4\)
6.1.5.3. Answer .
\(\displaystyle -12x^3y^4\)
\(\displaystyle \dfrac{1}{4ab^4}\)
6.1.5.5. Answer .
\(\displaystyle 4x^{10}y^{14}\)
\(\displaystyle x^4y\)
Skills Practice
6.1.5.7. Answer .
\(\displaystyle 9\)
\(\displaystyle \dfrac{1}{9}\)
\(\displaystyle 9\)
\(\displaystyle \dfrac{1}{9}\)
\(\displaystyle -9\)
\(\displaystyle \dfrac{-1}{9}\)
6.1.5.9. Answer .
\(\displaystyle 40\)
\(\displaystyle \dfrac{5}{8}\)
\(\displaystyle \dfrac{5}{8}\)
\(\displaystyle \dfrac{1}{40}\)
\(\displaystyle 40\)
\(\displaystyle \dfrac{8}{5}\)
6.1.5.11. Answer .
\(\displaystyle \dfrac{3}{4}\)
\(\displaystyle \dfrac{1}{8}\)
\(\displaystyle \dfrac{1}{2}\)
\(\displaystyle \dfrac{9}{4}\)
\(\displaystyle \dfrac{1}{6}\)
\(\displaystyle 2\)
\(\displaystyle \dfrac{4}{3}\)
\(\displaystyle 8\)
6.1.5.13. Answer .
\(\displaystyle \dfrac{1}{(m-n)^2}\)
\(\displaystyle \dfrac{1}{y^2}+\dfrac{1}{y^3}\)
\(\displaystyle \dfrac{2p}{q^4}\)
\(\displaystyle \dfrac{-5x^5}{y^2}\)
6.1.5.19. Answer .
\(\displaystyle \dfrac{20}{x^3}\)
\(\displaystyle \dfrac{1}{3u^{12}}\)
\(\displaystyle 5^8t\)
6.1.5.21. Answer .
\(\displaystyle \dfrac{1}{3}x+3x^{-1}\)
\(\displaystyle \dfrac{1}{4}x^{-2}-\dfrac{3}{2}x^{-1}\)
6.1.5.23. 6.1.5.25. Answer .
\(-4 - 2u^{-1} + 6u^{-2}\)
6.1.5.29. Answer .
\(\displaystyle 2.85 \times 10^2\)
\(\displaystyle 8.372 \times 10^6\)
\(\displaystyle 2.4 \times 10^{-2}\)
\(\displaystyle 5.23 \times 10^{-4}\)
Applications 6.1.5.31. Answer .
\(x\) \(1\) \(2\) \(4.5\) \(6.2\) \(9.3\)
\(g(x)\) \(1\) \(0.125\) \(0.011\) \(0.0042\) \(0.0012 \)
\(x\) \(1.5\) \(0.6\) \(0.1\) \(0.03\) \(0.002\)
\(f(x)\) \(0.30\) \(4.63\) \(1000\) \(37,037\) \(125 \times 10^6\)
6.1.5.33. Answer .
\(\displaystyle P = 0.355v^3\)
3.375
6.1.5.35. Answer .
\(\displaystyle d=50f^{-1}\)
The are of the aperture decreases by a factor of 0.5 at each \(f\) -stop.
6.1.5.36. Answer .
\(\displaystyle 1.905 \times 10^{13}\)
$57,552.87
6.2 Roots and Radicals 6.2.9 Problem Set 6.2
Warm Up 6.2.9.1. 6.2.9.3. Answer .
\(\displaystyle 1.414\)
\(\displaystyle 4.217\)
\(\displaystyle 1.125\)
\(\displaystyle 0.140\)
\(\displaystyle 2.782\)
\(\displaystyle 3.162\)
Skills Practice 6.2.9.5. Answer .
\(\displaystyle -3\)
\(\displaystyle undefined\)
\(\displaystyle -3\)
\(\displaystyle -3\)
6.2.9.7. Answer .
\(\displaystyle \sqrt{7}\)
\(\displaystyle 3\sqrt[4]{x} \)
\(\displaystyle \sqrt[4]{3x}\)
6.2.9.9. Answer .
\(\displaystyle 5^{1/2}\)
\(\displaystyle (4y)^{1/3}\)
\(\displaystyle 5x^{1/3} \)
6.2.9.11. Answer .
\(\dfrac{1}{4}x^{1/2}-2x^{-1/2}+\dfrac{1}{\sqrt{2}}x\)
6.2.9.13.
6.2.9.15. 6.2.9.17. 6.2.9.19.
6.2.9.21. Answer .
\(L=\dfrac{gT^2}{4\pi^2} \)
6.2.9.23. Answer .
\(M=\dfrac{d^3m}{16r^2}\)
6.2.9.25. 6.2.9.27. 6.2.9.29. Answer .
\(\displaystyle G(x) = 3.7x^{1/3} \)
\(\displaystyle H(x) = 85^{1/4}x^{1/4} \)
\(\displaystyle F(t) = 25t^{-1/5} \)
Applications 6.2.9.31. Answer .
\(L\) (feet)
\(200\) \(400\) \(600\) \(800\) \(1000\)
\(v_{\text{max}}\) (knots)
\(18.4\) \(26\) \(31.8\) \(36.8\) \(41.1\)
50.4 knots
31 knots, 62%
6.2.9.33. Answer .
\(\displaystyle T=\dfrac{2\pi}{\sqrt{32}}L^{1/2} \)
6.2.9.35. 6.2.9.36. Answer .
\(6.5\times 10^{-13}\) cm;
\(1.17\times 10^{-36} \text{ cm}^3\)
\(\displaystyle 1.8\times 10^{14} g/\text{cm}^3\)
Element
Carbon
Potassium
Cobalt
Technetium
Radium
Mass\(A\)
\(14\) \(40\) \(60\) \(99\) \(226\)
Radius, \(r\) \(10^{-13}\) cm)
\(3.1\) \(4.4\) \(5.1\) \(6\) \(7.9\)
6.2.9.37. 6.2.9.39.
6.3 Rational Exponents 6.3.7 Problem Set 6.3
Warm Up 6.3.7.1. Answer .
4; 4
15.59; 15.59
\(\displaystyle 8;~-81\)
6.3.7.3. Answer .
\(\displaystyle 2x^2y^9\)
\(\displaystyle -3a^2b^3\)
\(\displaystyle 4x^2y^6\)
Skills Practice 6.3.7.5. Answer .
\(\displaystyle \sqrt[4]{y^3}\)
\(\displaystyle \dfrac{1}{\sqrt[7]{a^2}}\)
\(\displaystyle \dfrac{1}{\sqrt[5]{s^3t^3}}\)
6.3.7.7. Answer .
\(\displaystyle y^{3/2}\)
\(\displaystyle 6a^{3/5}b^{3/5}\)
\(\displaystyle -2nq^{-11/8}\)
6.3.7.9. 6.3.7.11. 6.3.7.13.
6.3.7.15. 6.3.7.17. 6.3.7.19. 6.3.7.21.
6.3.7.23. 6.3.7.25. Answer .
\(2x^{1/2} - x^{1/4} - 1 \)
6.3.7.27. 6.3.7.29. Answer .
\(\dfrac{a^{2/3}+a^{1/3}-1}{a^{1/3}} \)
6.3.7.31. Answer .
\(x\) \(0\) \(1\) \(2\) \(3\) \(4\) \(5\) \(6\)
\(f(x)\) \(0\) \(1\) \(2.5\) \(4.3\) \(6.4\) \(8.5\) \(10.9\)
\(g(x)\) \(0\) \(1\) \(2.8\) \(5.2\) \(8\) \(11.2\) \(14.7\)
Applications 6.3.7.35. Answer .
\(t\) \(5\) \(10\) \(15\) \(20\)
\(I(t)\) \(131\) \(199\) \(254\) \(302\)
20 days
6.3.7.37. Answer .
\(A\) \(10\) \(100\) \(1000\) \(5000\) \(10,000\)
\(S\) \(25 \) \(42 \) \(69 \) \(98 \) \(115 \)
6.3.7.39. 6.3.7.41. Answer .
15 days, 28 days
\(\displaystyle \dfrac{I(m)\times W(m)}{m} = 0.18 m^{-0.041}\)
\(m^{-0.041}\) is close to 1
6.3.7.43. Answer .
\(\displaystyle p=K^{1/2}a^{3/2}\)
1.88 years
6.4 Working with Radicals 6.4.6 Problem Set 6.4
Warm Up 6.4.6.5. Answer .
\begin{equation*}
~\sqrt{ab} =\sqrt{a}\sqrt{b}~
\end{equation*}
\begin{equation*}
~\sqrt{\dfrac{a}{b}} =\dfrac{\sqrt{a}}{\sqrt{b}}~
\end{equation*}
Skills Practice
6.4.6.7. Answer .
\(\displaystyle 3\sqrt{2} \)
\(\displaystyle 2\sqrt[3]{3} \)
\(\displaystyle -2\sqrt[4]{4}=-2\sqrt{2} \)
6.4.6.9. Answer .
\(\displaystyle x^3 \sqrt[3]{x} \)
\(\displaystyle 3z\sqrt{3z} \)
\(\displaystyle 2a^2 \sqrt[4]{3a} \)
6.4.6.11. Answer .
\(\displaystyle 2\sqrt{4-x^2} \)
\(\displaystyle A\sqrt[3]{8+A^3} \)
6.4.6.13. Answer .
\(\displaystyle \sqrt[3]{ab^2} \)
\(\displaystyle x\sqrt{xy} \)
6.4.6.15. Answer .
\(\displaystyle 4\sqrt[3]{3} \)
\(\displaystyle -\sqrt[3]{2} \)
6.4.6.17. Answer .
\(\displaystyle 6\sqrt{3}+6\sqrt{5}\)
\(\displaystyle 3k\sqrt{3}-3k^2\sqrt{2}\)
6.4.6.19. Answer .
\(\displaystyle x-9\)
\(\displaystyle -4+\sqrt{6}\)
6.4.6.21. Answer .
\(\displaystyle 3-\sqrt{5}\)
\(\displaystyle \dfrac{-4+\sqrt{2}}{2}\)
\(\displaystyle \dfrac{2a-\sqrt{2}}{2a}\)
6.4.6.23. Answer .
\(\displaystyle \dfrac{\sqrt{14x}}{6}\)
\(\displaystyle \dfrac{\sqrt{2ab}}{b}\)
6.4.6.25. Answer .
\(\displaystyle -2{1-\sqrt{3}}\)
\(\displaystyle \dfrac{x(x+\sqrt{3}}{x^2-3}\)
Applications 6.4.6.27. Answer .
\(x^2+4x=(4-4\sqrt{5}+5)+(8+4\sqrt{5})=1\)
6.4.6.29. Answer .
\(\displaystyle \dfrac{w\sqrt{3}}{2}\)
\(\displaystyle \dfrac{w^2\sqrt{3}}{4}\)
6.5 Radical Equations 6.5.6 Problem Set 6.5
Warm Up 6.5.6.1. Answer .
\(\displaystyle z=4\)
\(\displaystyle w=8\)
6.5.6.3. 6.5.6.5. Answer .
\(x\) \(y\)
\(-25\) \(6.92\)
\(-20\) \(6.71\)
\(-15\) \(6.47\)
\(-10\) \(6.15\)
\(-5\) \(3.21\)
\(0\) \(4\)
\(5\) \(2.29\)
\(10\) \(1.85\)
\(15\) \(1.53\)
\(20\) \(1.29\)
\(\displaystyle -8\)
Skills Practice
6.5.6.7. 6.5.6.9. 6.5.6.11. 6.5.6.13. 6.5.6.15. 6.5.6.17. Answer .
\(\displaystyle 2\abs{x}\)
\(\displaystyle \abs{x-5}\)
\(\displaystyle \abs{x-3}\)
Applications 6.5.6.19. Answer .
1.25 mi; 6600 ft
\(\displaystyle h=(\dfrac{d}{89.4})^2\)
6.5.6.21. Answer .
339.39 cubic in
\(\displaystyle V=12.57r^3\)
6.5.6.23. Answer .
\(b= \pm \sqrt{a^2-c^2}\)
6.5.6.25. Answer .
\(W=\dfrac{v}{1-(\dfrac{D}{S})^3}\)
6.6 Chapter 6 Summary and Review 6.6.3 Chapter 6 Review Problems
6.6.3.1. Answer .
\(\displaystyle \dfrac{1}{81}\)
\(\displaystyle \dfrac{1}{64}\)
6.6.3.2. Answer .
\(\displaystyle 9\)
\(\displaystyle 75\)
6.6.3.3. Answer .
\(\displaystyle \dfrac{1}{243m^5}\)
\(\displaystyle \dfrac{-7}{y^8}\)
6.6.3.4. Answer .
\(\displaystyle \dfrac{1}{a}+\dfrac{1}{a^2}\)
\(\displaystyle \dfrac{3r^2}{q^9}\)
6.6.3.5. Answer .
\(\displaystyle \dfrac{2}{c^3}\)
\(\displaystyle \dfrac{99}{z^2}\)
6.6.3.6. Answer .
\(\displaystyle \dfrac{d^8}{16k^{12}}\)
\(\displaystyle \dfrac{2}{5}w^{14}\)
6.6.3.7. Answer .
\(1.018 \times 10{-9}~\) sec, or 0.000 000 001 018 sec
8 min 20 sec
6.6.3.8. Answer .
1,200,000,000,000 hr, or 78,904,109,590 yr
6.6.3.9. Answer .
5000 sec, or 83 min
\(\displaystyle \dfrac{1}{10}\)
42 yr
6.6.3.10. Answer .
Planet
Density
Mercury
5426
Venus
5244
Earth
5497
Mars
3909
Jupiter
1241
Saturn
620
Uranus
1238
Neptune
1615
Pluto
2355
Mercury, Venus, Earth, and Mars
6.6.3.11. Answer .
\(\displaystyle 25\sqrt{m} \)
\(\displaystyle \dfrac{8}{\sqrt[3]{n}} \)
6.6.3.12. Answer .
\(\displaystyle \sqrt[3]{(13d)^3}\)
\(\displaystyle 6\sqrt[5]{x^2y^3} \)
6.6.3.13. Answer .
\(\displaystyle \dfrac{1}{\sqrt[4]{27q^3}} \)
\(\displaystyle 7\sqrt{u^3v^3} \)
6.6.3.14. Answer .
\(\displaystyle \sqrt{a^2+b^2} \)
\(\displaystyle \sqrt[4]{16-x^2} \)
6.6.3.15. Answer .
\(\displaystyle 2x^{2/3} \)
\(\displaystyle \dfrac{1}{4}x^{1/4} \)
6.6.3.16. Answer .
\(\displaystyle z^{5/2} \)
\(\displaystyle z^{4/3} \)
6.6.3.17. Answer .
\(\displaystyle 6b^{-3/4} \)
\(\displaystyle \dfrac{-1}{3}b^{-1/3} \)
6.6.3.18. Answer .
\(\displaystyle -4a^{-1/2} \)
\(\displaystyle 2a^{-3/2} \)
6.6.3.19. 6.6.3.20. Answer .
Height: 2.673 in; diameter: 5.346 in
6.6.3.21. 6.6.3.22. 6.6.3.23. 6.6.3.25. 6.6.3.27. Answer .
It is the cost of producing the first ship.
\(C = \dfrac{12}{ \sqrt[8]{x}} \) million
About $11 million; about 8.3% ; about 8.3%>
6.6.3.29. Answer .
\(\displaystyle 4096\)
\(\displaystyle \dfrac{1}{8}\)
\(\displaystyle 36\sqrt{3} \approx 62.35\)
\(\displaystyle 400,000\)
6.6.3.30. Answer .
\(\displaystyle -27\)
\(\displaystyle \dfrac{-3}{4}\)
\(\displaystyle -3\sqrt[3]{400} \approx -22.1\)
\(\displaystyle -300\)
6.6.3.31. 6.6.3.32. 6.6.3.33. 6.6.3.34. 6.6.3.35. 6.6.3.36. 6.6.3.37. 6.6.3.38. 6.6.3.39. 6.6.3.40. 6.6.3.41. 6.6.3.42.
6.6.3.43. 6.6.3.44. Answer .
\(r=\dfrac{\pm \sqrt{3q^2-6q+7}}{2} \)
6.6.3.45. Answer .
\(p=\pm 2 \sqrt{R^2-R} \)
6.6.3.46.
6.6.3.47. Answer .
\(\displaystyle \dfrac{5p^4}{a^2}\sqrt{5p}\)
\(\displaystyle \dfrac{2}{w^2}\sqrt[3]{3v^2}\)
6.6.3.48. Answer .
\(\displaystyle a^2b\)
\(\displaystyle xy\)
6.6.3.49. Answer .
\(\displaystyle 2\sqrt[3]{a^3-2b^6}\)
\(\displaystyle -4ab^2\sqrt[3]{2} \)
6.6.3.50. Answer .
\(\displaystyle 2t\sqrt{1+6t^4}\)
\(\displaystyle 4t^4\sqrt{6} \)
6.6.3.51. Answer .
\(\displaystyle x^2-4x\sqrt{x}+4x\)
\(\displaystyle x^2-4x\)
6.6.3.52. Answer .
\(\displaystyle 14-4\sqrt{6}\)
\(\displaystyle 2a-4b\)
6.6.3.53. Answer .
\(\displaystyle \dfrac{7\sqrt{5y}}{5y}\)
\(\displaystyle 3\sqrt{2d}\)
6.6.3.54. Answer .
\(\displaystyle \dfrac{\sqrt{33rs}}{11s}\)
\(\displaystyle \dfrac{\sqrt{13m}}{m}\)
6.6.3.55. Answer .
\(\displaystyle \dfrac{-3\sqrt{a}+6}{a-4}\)
\(\displaystyle \dfrac{-3\sqrt{z}-12}{z-16}\)
6.6.3.56. Answer .
\(\displaystyle \dfrac{2x^2+x\sqrt{3}-3}{x^2-3}\)
\(\displaystyle \dfrac{5m^2-7m\sqrt{3}+6}{25m^2-12}\)
7 Exponential Functions 7.1 Exponential Growth and Decay 7.1.7 Problem Set 7.1
Warm Up 7.1.7.1. Answer .
$28
#31.36
No. It increase by 12% of different amounts.
7.1.7.3.
7.1.7.5. 7.1.7.7. 7.1.7.9. Answer .
\(-2.14\text{;}\) \(0.14\)
Skills Practice 7.1.7.11. Answer .
\(P = 1200 + 150t\text{;}\) 1650
\(P = 1200\cdot 1.5^t\text{;}\) 4050
7.1.7.13. Answer .
\(V = 18,000 - 2000t\text{;}\) $8000
\(V = 18,000\cdot 0.8^t\text{;}\) $5898.24
7.1.7.15. Answer .
20%, 2%, 7.5%, 100%, 115%
7.1.7.17. Answer .
\(\displaystyle P_0 = 4,~ b = 2^{1/3}\)
\(\displaystyle P(t) = 4\cdot 2^{t/3}\)
7.1.7.18. Answer .
Initial value
\(80\text{,}\) decay factor
\(\frac{1}{2}\)
\(\displaystyle f(x) = 80\cdot \left(\dfrac{1}{2} \right)^x \)
7.1.7.19. Answer .
The growth factor is
\(1.2\text{.}\)
\(x\) \(0\) \(1\) \(2\) \(3\) \(4\)
\(Q\) \(20\) \(24\) \(28.8\) \(34.56\) \(41.47\)
7.1.7.20. Answer .
The decay factor is
\(0.8\text{.}\)
\(w\) \(0\) \(1\) \(2\) \(3\) \(4\)
\(N\) \(120\) \(96\) \(76.8\) \(61.44\) \(49.15\)
7.1.7.21. Answer .
The decay factor is
\(0.8\text{.}\)
\(t\) \(0\) \(1\) \(2\) \(3\) \(4\)
\(C\) \(10\) \(8\) \(6.4\) \(5.12\) \(4.10\)
7.1.7.22. Answer .
The growth factor is
\(1.1\text{.}\)
\(n\) \(0\) \(1\) \(2\) \(3\) \(4\)
\(B\) \(200\) \(220\) \(242\) \(266.2\) \(292.82\)
Applications
7.1.7.23. Answer .
Years after 2010
\(0\) \(1\) \(2\) \(3\) \(4\)
Windsurfers
\(1500\) \(1680\) \(1882\) \(2107\) \(2360\)
\(\displaystyle S(t)=1200(1.12)^t\)
2644; 5844
7.1.7.24. Answer .
Years after 1983
\(0\) \(5\) \(10\) \(15\) \(20\)
Value of house
\(20,000\) \(25,526\) \(32,578\) \(41,579\) \(53,066\)
\(\displaystyle V(t)=200,000(1.05)^t\)
$359,171.27; $458,403.66
7.1.7.25. Answer .
Weeks
\(0\) \(6\) \(12\) \(18\) \(24\)
Bees
\(2000\) \(5000\) \(12,500\) \(31,250\) \(78,125\)
\(\displaystyle P(t)=2000(2.5)^{t/6}\)
7.1.7.27. Answer .
Weeks
\(0\) \(2\) \(4\) \(6\) \(8\)
Mosquitos
\(250,000\) \(187,500\) \(140,625\) \(105,469\) \(79,102\)
\(\displaystyle P(t)=250,000(0.75)^{t/2}\)
162,280; 68,504
7.1.7.29. Answer .
Years
\(0\) \(3\) \(6\) \(9\) \(12\)
Value of boat
\(15,000\) \(13,500\) \(12,150\) \(10,935\) \(9841.50\)
\(\displaystyle V(t)=15,000(0.885)^t\)
$4995.52; $4421.04
7.1.7.31. Answer .
\(\displaystyle P(t)=1,545,387 b^t\)
\(\displaystyle b=1.049;~ r=4.9\%\)
3,167,157
7.1.7.33. Answer .
365
\(\displaystyle N(t)=365(0.356)^t\)
0.03
7.1.7.35. 7.1.7.37. Answer .
39; 1.045
36; 1.047
Species B
7.2 Exponential Functions 7.2.6 Problem Set 7.2
Warm Up
7.2.6.1. Answer .
\(\displaystyle 3^{x+4}\)
7.2.6.3. Answer .
\(\displaystyle b^{-2t} \)
\(\displaystyle b^{t/2} \)
Skills Practice
7.2.6.7. 7.2.6.8. 7.2.6.9. 7.2.6.11. 7.2.6.13. 7.2.6.17. Answer .
\((0,26)\text{;}\) increasing
\((0,1.2)\text{;}\) decreasing
\((0,75)\text{;}\) decreasing
\((0,\frac{2}{3}) \text{;}\) increasing
7.2.6.18. 7.2.6.19. Answer .
\(x\) \(-3\) \(-2\) \(-1\) \(0\) \(1\) \(2\) \(3\)
\(f(x)=3^x \) \(\frac{1}{27} \) \(\frac{1}{9} \) \(\frac{1}{3} \) \(1\) \(3\) \(9\) \(27\)
\(g(x)=\left(\frac{1}{3} \right)^x \) \(27\) \(9\) \(3\) \(1\) \(\frac{1}{3} \) \(\frac{1}{9} \) \(\frac{1}{27} \)
7.2.6.21. Answer .
Because they are defined by equivalent expressions, (b), (c), and (d) have identical graphs.
7.2.6.25. Answer .
\(\displaystyle P_0 = 800\)
\(x\) \(0\) \(1\) \(2\)
\(g(x)\) \(800\) \(200\) \(50\)
\(\displaystyle a = \dfrac{1}{4}\)
\(\displaystyle g(x) = 800(\dfrac{1}{4})^x\)
7.2.6.27. Answer .
Exponential
\(P=\frac{1}{4} \cdot 2^x\)
Applications 7.2.6.28. Answer .
\(\displaystyle V(t) = 20,000(0.8)^{t/3}\)
7.2.6.29. Answer .
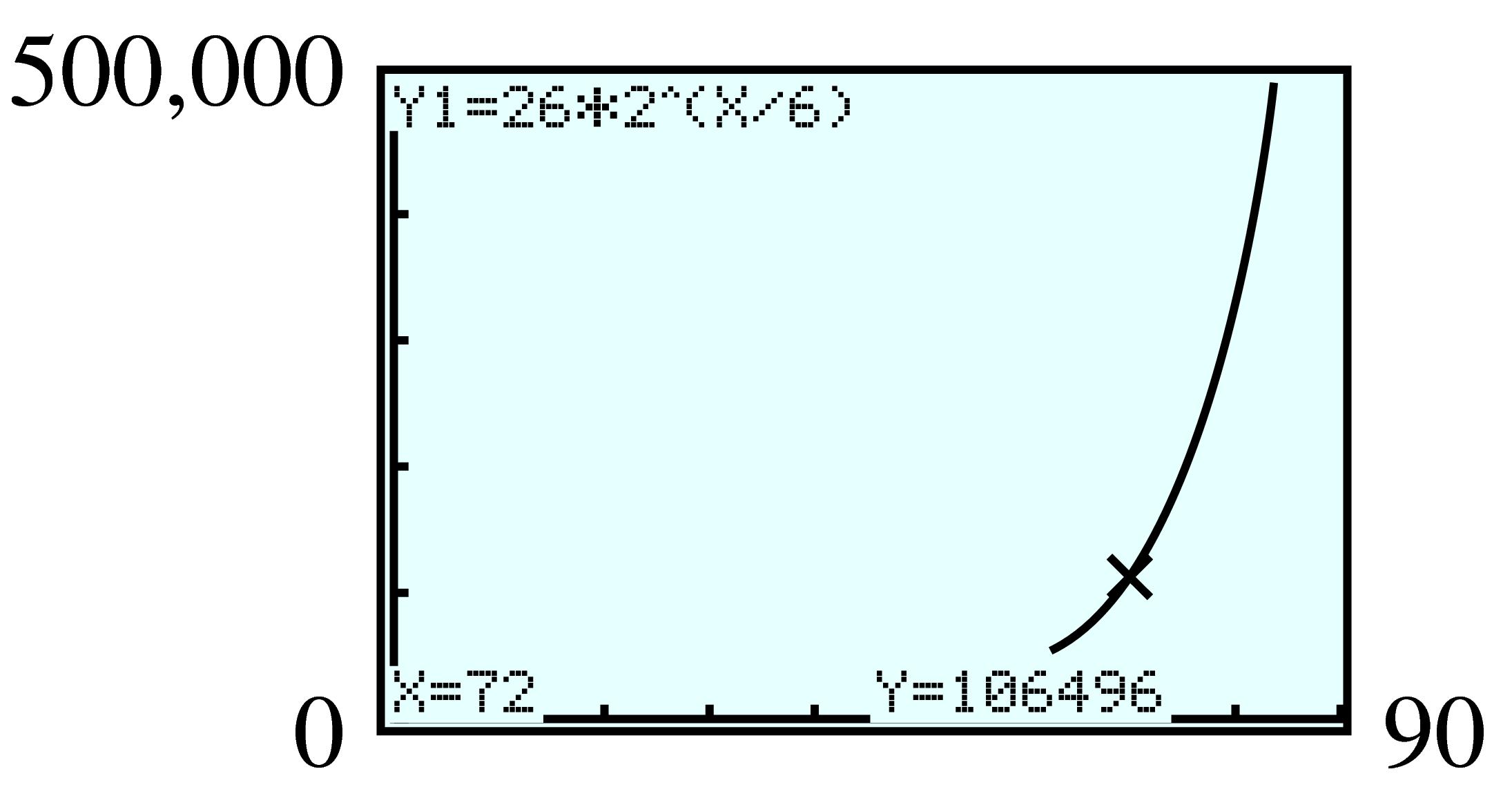
\(\displaystyle N(t) = 26(2)^{t/6}\)
7.2.6.30. Answer .
\(\displaystyle F_0=400\)
\(\displaystyle F(p) = 440(1.06)^p\)
7.2.6.31. Answer .
\(\displaystyle S_0=150\)
\(\displaystyle b\approx 0.55\)
\(\displaystyle S(d) = 150(0.55)^d\)
7.2.6.32. Answer .
\(x\) \(f(x)=x^2\) \(g(x)=2^x \)
\(-2\) \(4\) \(\frac{1}{4} \)
\(-1\) \(1\) \(\frac{1}{2} \)
\(0\) \(0\) 1
\(1\) \(1\) \(2\)
\(2\) \(4\) \(4\)
\(3\) \(9\) \(8\)
\(4\) \(16\) \(16\)
\(5\) \(25\) \(32\)
\(\displaystyle x = -0.77,~2,~4\)
\(\displaystyle (-0.77, 2) \cup (4,\infty)\)
7.3 Logarithms 7.3.7 Problem Set 7.3
Warm Up 7.3.7.1. Answer .
\(\displaystyle P(t)=300(1.15)^t\)
\(\displaystyle 500=300(1.15)^t\)
\(\displaystyle t \approx 3.65 \)
Skills Practice
7.3.7.3. 7.3.7.5. Answer .
\(\displaystyle \dfrac{1}{2}\)
7.3.7.7. 7.3.7.9. Answer .
\(\displaystyle 3 \lt x \lt 4\)
\(\displaystyle -1 \lt y \lt 0\)
7.3.7.11. 7.3.7.13. 7.3.7.15. 7.3.7.17. Answer .
\(\displaystyle \log_t {(16)} = \dfrac{3}{2}\)
\(\displaystyle \log_{0.8}{(M)} = 1.2\)
7.3.7.19. Answer .
\(\displaystyle 16^w = 256\)
b^{-2} = 9
7.3.7.21. Answer .
\(\displaystyle x=\log_4{(2.5)} \approx 2.7\)
\(\displaystyle x=\log_2{(0.2)} \approx -2.3\)
Applications 7.3.7.25. 7.3.7.29. 7.3.7.31. Answer .
\(\displaystyle \sqrt[3]{16} \approx 2.52\)
7.4 Properties of Logarithms 7.4.5 Problem Set 7.4
Warm Up 7.4.5.1. Answer .
\(\displaystyle \log_8 {\left(\dfrac{1}{2}\right)} = \dfrac{-1}{3}\)
\(\displaystyle \log_5 {(46)} = x\)
7.4.5.3. Answer .
\(2;~6;~8~\) Property (1)
7.4.5.5. Answer .
\(8;~5;~3~\) Property (2)
7.4.5.7. Answer .
\(\displaystyle 10^{15}\)
7.4.5.9. 7.4.5.11. Answer .
\(\displaystyle \log {(24)} \approx 1.38\)
\(\displaystyle \log {(240)} \approx 2.38\)
\(\displaystyle \log {(230)} \approx 2.36\)
None are equal.
Skills Practice
7.4.5.13. Answer .
\(\displaystyle \log_b {(2)} + \log_b {(x)}\)
\(\displaystyle \log_b {(2)} - \log_b {(x)}\)
\(\displaystyle 3\log_b {(x)}\)
\(\displaystyle \dfrac{2}{3}\log_b {(x)}\)
7.4.5.15. Answer .
\(\displaystyle \log_3 {(3)} + 4\log_3 {(x)} \)
\(\displaystyle (1/t)\log_5{(1.1)}\)
\(\displaystyle t\left(\log_b {(4)} + \log_b {(t)} \)
\(\displaystyle \log_2 {(5)} + x\)
7.4.5.17. Answer .
\(\displaystyle \log_b {(4)}\)
\(\displaystyle \log_4{(x^2y^3)} \)
7.4.5.19. Answer .
\(\displaystyle \log {(2x^{5/2})} \)
\(\displaystyle \log {(t-4)} \)
7.4.5.25. 7.4.5.27. 7.4.5.29. 7.4.5.31. Answer .
\(\displaystyle -0.9163\)
Applications 7.4.5.37. Answer .
\(\displaystyle S (t) = S_0(1.09)^t\)
7.4.5.39. Answer .
\(\displaystyle C(t) = 0.7(0.80)^t\)
7.4.5.41. Answer .
\(\displaystyle S(t) = S_0 \cdot 0.9527^t\)
7.4.5.43. Answer .
\(k=\dfrac{\log{\left(\dfrac{N}{N_0}\right)}}{t \log {(a)}} \)
7.4.5.45. Answer .
\(t=\dfrac{1}{k}\log{\left(\dfrac{A}{A_0}+1\right)} \)
7.5 Exponential Models 7.5.5 Problem Set 7.5
Warm Up Skills Practice 7.5.5.13. Answer .
\(\displaystyle y=2.6-1.3x\)
\(\displaystyle y=2.5(0,5)^x\)
Applications
7.5.5.15. Answer .
\(P(t)=2000(2^{t/5};~\) 14.9%
7.5.5.17. Answer .
\(D(t)=D_0(0,5^{t/18};~\) 3.8%
7.5.5.19. Answer .
\(\displaystyle P = P_0 (2)^{t/25 }\)
7.5.5.21. Answer .
\(\dfrac{\log {(0.5)}}{\log {(0.946)}}\approx 12.5 \) hours
7.5.5.23. Answer .
\(\displaystyle D(t)=D_0(0.5)^{t/15}\)
After 89.5 years, or in 2060
7.5.5.25. Answer .
\(\displaystyle A = A_0 \left(\dfrac{1}{2} \right)^{t/5730}\)
7.6 Chapter 7 Summary and Review 7.6.3 Chapter 7 Review Problems
7.6.3.1. Answer .
\(\displaystyle D = 8(1.5)^{t/5}\)
7.6.3.3. Answer .
\(\displaystyle M = 100(0.85)^t\)
7.6.3.13. 7.6.3.15. 7.6.3.17. 7.6.3.21. Answer .
\(\log_{0.3}{(x + 1)} = -2\)
7.6.3.23. 7.6.3.25. 7.6.3.27. Answer .
\(\dfrac{\log {(5.1)}}{1.3}\approx 0.5433 \)
7.6.3.29. Answer .
\(\dfrac{\log {(2.9/3)}}{-0.7}\approx 0.21 \)
7.6.3.31. 7.6.3.32. 7.6.3.33. 7.6.3.34.
7.6.3.35. Answer .
\(\log_b {(x)} + \dfrac{1}{3} \log_b {(y)} - 2 \log_b {(z)}\)
7.6.3.37. Answer .
\(\dfrac{4}{3} \log {(x)} -\dfrac{1}{3} \log {(y)}\)
7.6.3.39. Answer .
\(\log{\right(\sqrt[3] {\dfrac{x}{y^{2}}}\left)} \)
7.6.3.41. Answer .
\(\log {\left(\dfrac{1}{8}\right)} \)
7.6.3.43. Answer .
\(\dfrac{\log {(63)}}{\log {(3)}}\approx 3.77 \)
7.6.3.45. Answer .
\(\dfrac{\log {(50)}}{-0.3\log {(6)}}\approx -7.278 \)
7.6.3.47. Answer .
\(\dfrac{\log{(N/N_0)}}{k}\)
7.6.3.49. 7.6.3.51. Answer .
\(\displaystyle C = 90(1.06)^t\)
8 Polynomial and Rational Functions 8.1 Polynomial Functions 8.1.10 Problem Set 8.1
Warm Up 8.1.10.1. Answer .
\(\displaystyle a^2 + 2ab + b^2\)
\(\displaystyle a^2 - 2ab + b^2\)
8.1.10.3. Answer .
\(\displaystyle (x-7)^2\)
cannot be factored
\(\displaystyle (x+3)^2\)
\(\displaystyle (x+8)(x-8)\)
Skills Practice 8.1.10.5. Answer .
(b) and (c) are not polynomials; they have variables in a denominator.
8.1.10.7. Answer .
\(\displaystyle -1.9x^3+x+6.4\)
\(\displaystyle -2x^2+6xy+2y^3\)
8.1.10.9. 8.1.10.11. Answer .
\(\displaystyle 6a^4-5a^3-5a^2+5a-1\)
\(\displaystyle y^4+5y^3-20y-16\)
8.1.10.13. Answer .
\(\displaystyle 1+15\sqrt{t}+75t+125t\sqrt{t}\)
\(\displaystyle 1-\dfrac{9}{a}+\dfrac{27}{a^2}-\dfrac{27}{a^3}\)
8.1.10.15. Answer .
\(\displaystyle 27a^3-8b^3\)
\(\displaystyle 8a^3 + 27b^3\)
8.1.10.17. 8.1.10.19. Answer .
\((3a+4b)(9a^2-12ab+16b^2)\)
8.1.10.21. Answer .
\((4t^3+w^2)(16t^6-4t^3w^2+w^4)\)
Applications 8.1.10.23. Answer .
length: \(w+3\text{;}\) height: \(w-2\)
\(\displaystyle w^3+w^2-6w\)
\(\displaystyle 5w^2+w-12\)
8.1.10.25. Answer .
\(\displaystyle \dfrac{2}{3}\pi r^3+\pi r^2h \)
\(\displaystyle V(r)=\dfrac{14}{3}\pi r^3 \)
8.1.10.27. Answer .
\(0\le x \le 9\text{;}\) \(R\ge 0\) for these values
\(\dfrac{28}{3} \) points
8.1.10.29. 8.1.10.31. Answer .
\(\displaystyle 6 + x + 5x^2\)
\(\displaystyle 4 - 7x^2 - 8x^4\)
8.2 Algebraic Fractions 8.2.5 Problem Set 8.2
Warm Up
8.2.5.1. Answer .
\(\dfrac{-3}{5} \text{,}\) \(\dfrac{3}{7} \)
\(\displaystyle -1\)
8.2.5.3. Answer .
\(\dfrac{-4}{3} \text{,}\) \(\dfrac{40}{399} \)
\(\displaystyle 0\)
8.2.5.5. Answer .
\(\displaystyle \dfrac{5}{x}\)
\(\displaystyle \dfrac{12b}{7} \)
8.2.5.7. Answer .
\(\displaystyle \dfrac{-8}{5} \)
\(\displaystyle \dfrac{a}{9}\)
Skills Practice 8.2.5.9.
8.2.5.17. 8.2.5.19. 8.2.5.21. 8.2.5.23. 8.2.5.25. 8.2.5.27. Answer .
\(\dfrac{4z^2+6z+9}{2z+3}\)
Applications 8.2.5.29. Answer .
The time increases. If the current is 10 mph, the team will not be able to row upstream
8.2.5.31. Answer .
\(\displaystyle 0\le p \lt 100\)
\(p\) \(0\) \(25\) \(50\) \(75\) \(90\) \(100\)
\(C\) \(0\) \(120\) \(360\) \(1080\) \(3240\) \(-- \)
\(\displaystyle p\lt 80\%\)
\(p=100\text{:}\) The cost of extracting more ore grows without bound as the amount extracted approaches 100%.
8.2.5.33. Answer .
\(\dfrac{200}{2x-1} \) square centimeters
8; If
\(x=13\text{,}\) the area of the cross-section is 8
\(\text{cm}^2\text{.}\)
8.2.5.35. Answer .
\(4500+\dfrac{3000}{x} \text{;}\) \(C(x) = 6x + 4500 + \dfrac{3000}{x} \)
\(x\) \(20\) \(40\) \(60\) \(80\) \(100\)
\(C\) \(4770 \) \(4815 \) \(5018 \) \(5130 \)
The graph of
\(C\) approaches the line as an asymptote.
8.3 Operations on Algebraic Fractions 8.3.9 Problem Set 8.3
Warm Up
8.3.9.1. Answer .
\(\displaystyle \dfrac{4}{15} \)
\(\displaystyle \dfrac{2z}{3w}\)
8.3.9.3. 8.3.9.5. Answer .
\(\displaystyle \dfrac{1}{6}\)
\(\displaystyle \dfrac{1}{6y^2}\)
Skills Practice 8.3.9.7. Answer .
\(\displaystyle \dfrac{-36a^2}{7} \)
\(\displaystyle \dfrac{8b}{3b+3}\)
\(\displaystyle \dfrac{v^2}{1-v^2}\)
8.3.9.9. 8.3.9.11. 8.3.9.13. Answer .
\(\dfrac{6x(x-2)(x-1)^2}{(x^2-8)(x^2-2x+4)}\)
8.3.9.15. 8.3.9.17. 8.3.9.19. 8.3.9.21. Answer .
\(\dfrac{(z+2)^2}{z^2(2z-1)}\)
8.3.9.23.
8.3.9.29. 8.3.9.31. 8.3.9.33. Answer .
\(\dfrac{h^2+2h-3}{h+2}\)
8.3.9.35. Answer .
\(\dfrac{6x-x^2-4}{x(x-2)}\)
8.3.9.37. 8.3.9.39. Answer .
\(\dfrac{5k+1}{k(k-3)(k+1)}\)
8.3.9.41. Answer .
\(\dfrac{3y-3y^2}{(y+1)(2y-1)}\)
Applications
8.3.9.47. 8.3.9.49. Answer .
\(\dfrac{2L}{c}+\dfrac{2LV^2}{c^3}\)
8.3.9.51. Answer .
\(\dfrac{3q}{8\pi R}-\dfrac{a^2q}{8 \pi R^3}\)
8.3.9.53. Answer .
\(-8t +\dfrac{1}{4} - \dfrac{3}{t}\)
8.3.9.55. Answer .
\(\displaystyle \dfrac{x}{2}\)
\(\displaystyle 2x\)
\(\displaystyle \dfrac{1}{2x}\)
8.3.9.57. Answer .
\(\displaystyle \dfrac{1}{a+b}\)
\(\displaystyle \dfrac{3}{4(a+b)}\)
\(\displaystyle \dfrac{4}{3(a+b)}\)
8.3.9.59. 8.3.9.61. Answer .
\(\dfrac{4L-R^2C}{4L^2C}\)
8.3.9.63. Answer .
\(\dfrac{2r^2_2ra+a^2}{a^2}\)
8.3.9.65. Answer .
\(\dfrac{144}{x^2-2x}\) sq ft
\(\displaystyle \dfrac{48x-48}{x^2-2x} ft\)
8.3.9.67. Answer .
\(\dfrac{900}{400+w}\) hr
\(\dfrac{900}{400-w}\) hr
Orville, by \(\dfrac{1800w}{160,000-w^2}\) hr
8.4 More Operations on Fractions 8.4.5 Problem Set 8.4
Warm Up
8.4.5.1. Answer .
\(\dfrac{2x^2+x-2}{x(x-1)} \)
8.4.5.3. Skills Practice
8.4.5.5. 8.4.5.7. 8.4.5.9. 8.4.5.11. 8.4.5.13. 8.4.5.15.
8.4.5.17. Answer .
\(\dfrac{1}{2}x^2\dfrac{1}{2}-\dfrac{1}{3x^2}\)
8.4.5.19.
8.4.5.21. Answer .
\(2y+5+\dfrac{2}{2y+1)}\)
8.4.5.23. Answer .
\(4z^3-2z^2+3z+1+\dfrac{2}{2z+1}\)
Applications 8.4.5.25. Answer .
\(\overline{PQ}\) and
\(overline{RS}: ~\dfrac{b}{a}\text{;}\) \(\overline{QR}\) and
\(overline{SP}: ~\dfrac{b}{a}\)
8.4.5.27. Answer .
\(\displaystyle \dfrac{1}{f}=\dfrac{2q+60}{q^2+60q} \)
\(\displaystyle f=\dfrac{q^2+60q}{2q+60} \)
8.4.5.29. 8.4.5.31. 8.4.5.33. 8.4.5.35.
8.4.5.37. Answer .
\(\dfrac{x^2+y^2}{x^2y^2}\)
8.4.5.39. 8.4.5.41.
8.4.5.43. 8.4.5.45. Answer .
\(\dfrac{2\sqrt{3}+\sqrt{6}}{9}\)
8.4.5.47. Answer .
\(\dfrac{6\sqrt{3}+7\sqrt{2}}{5}\)
8.5 Equations with Fractions 8.5.8 Problem Set 8.5
Warm Up
8.5.8.1. 8.5.8.3. 8.5.8.5. Answer .
\(\pm\sqrt{\dfrac{15}{8}} \)
8.5.8.7. Answer .
\(\dfrac{1800}{1849}\approx 0.97 \)
Skills Practice
8.5.8.9. 8.5.8.11. 8.5.8.13. 8.5.8.15. 8.5.8.17. Answer .
We don’t multiply by the LCD in addition problems.
8.5.8.19. 8.5.8.21. 8.5.8.23. Applications 8.5.8.25. 8.5.8.27. 8.5.8.29. Answer .
\(168=\dfrac{72p}{100-p}\text{;}\) \(p=70\%\)
8.5.8.31. Answer .
0.268
\(\displaystyle \dfrac{44+x}{164+x}\)
21
8.5.8.33. Answer .
\(\displaystyle t=\dfrac{144}{v-20}\)
\(\displaystyle t=\dfrac{144}{v+20}\)
\(\displaystyle (100,3)\)
\(\displaystyle t=\dfrac{144}{v-20} + t=\dfrac{144}{v+20} = 3\)
100 mph
8.5.8.35. Answer .
\(28 \dfrac{1}{3}\) miles
8.5.8.37. Answer .
\(\displaystyle AE = 1,~ DE = x - 1,~ CD = 1\)
\(\displaystyle \dfrac{1}{x}=\dfrac{x-1}{x} \)
\(\displaystyle \dfrac{1+\sqrt{5}}{2} \)
8.5.8.39. Answer .
Because
\(x=1\text{,}\) dividing by
\(x-1\) in the fourth step is dividing by
\(0\text{.}\)
8.5.8.41. Answer .
\(\displaystyle x=\dfrac{1}{2} \)
8.6 Chapter 8 Summary and Review 8.6.3 Chapter 8 Review Problems
8.6.3.3. Answer .
\((2x-3z)(4x^2+6xz+9z^2)\)
8.6.3.5. Answer .
\(\displaystyle \dfrac{1}{6}n^3-\dfrac{1}{2}n^2+\dfrac{1}{3}n \)
8.6.3.7. Answer .
\(\displaystyle V=\dfrac{\pi h^3}{4} \)
\(2\pi\text{ cm}^3 \approx 6.28\text{ cm}^3 \text{;}\) \(16\pi\text{ cm}^3 \approx 50.27\text{ cm}^3 \)
8.6.3.9. Answer .
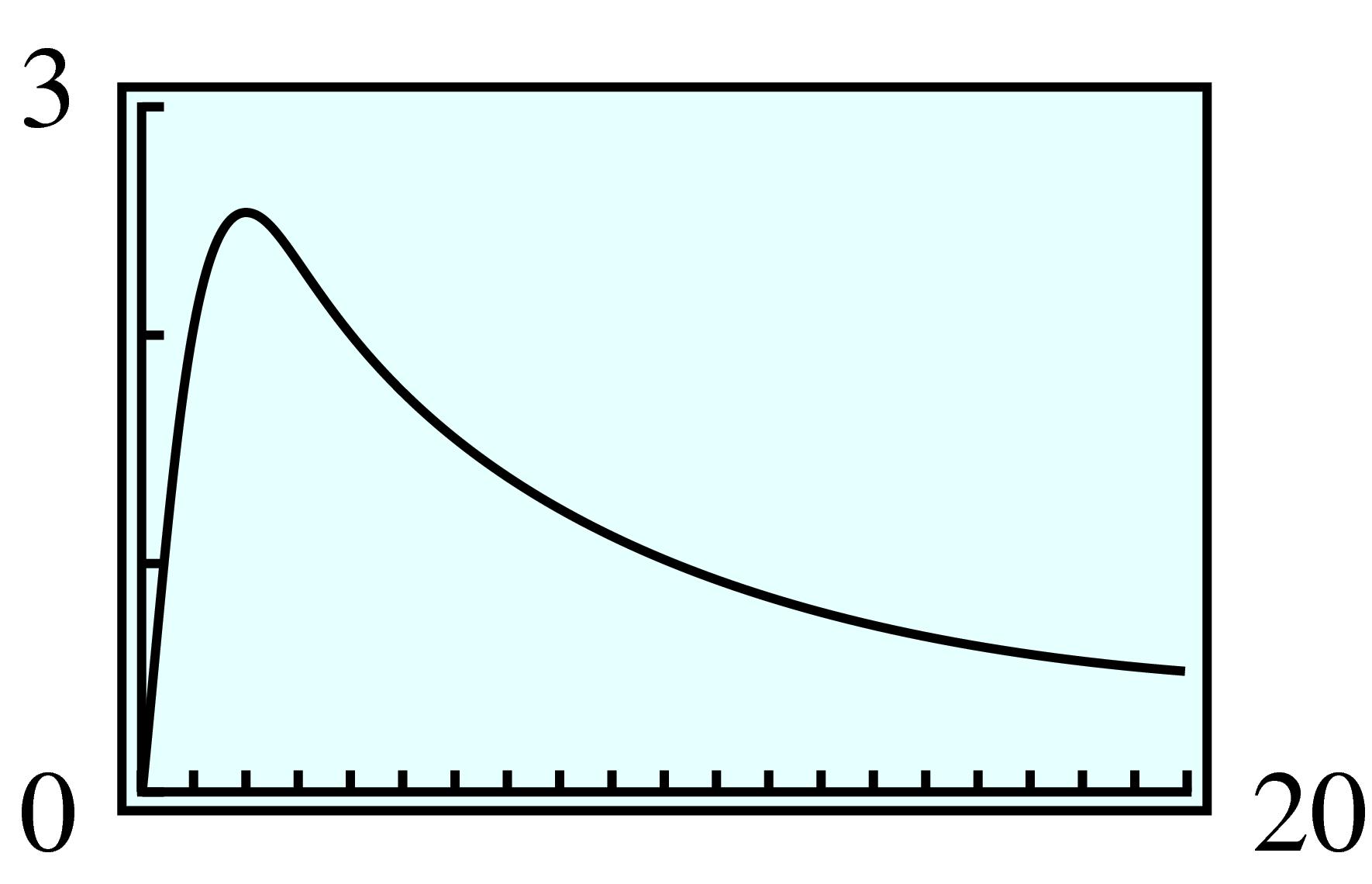
During month 6. The number of members eventually decreases to zero.
8.6.3.11. Answer .
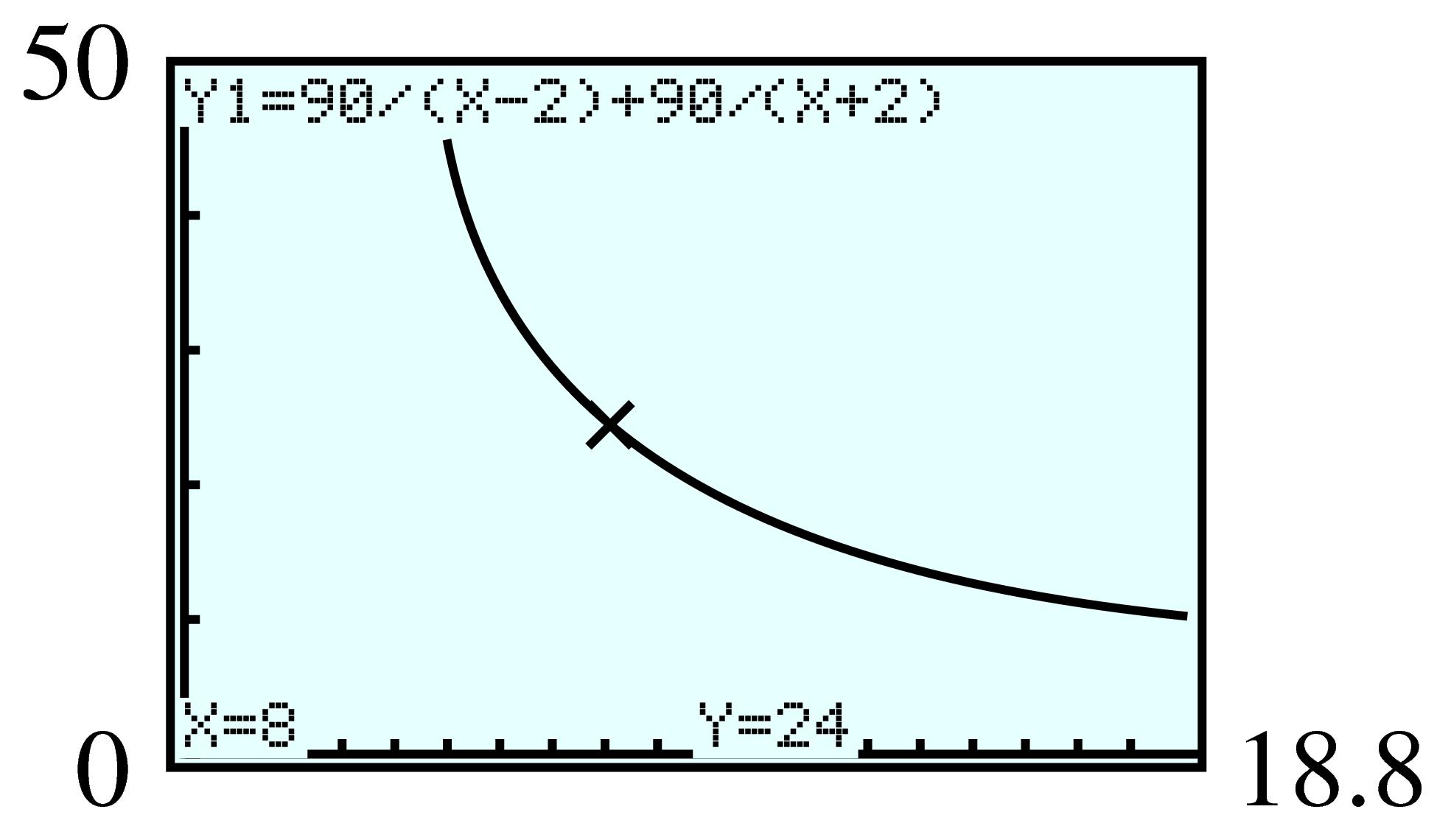
\(\displaystyle t_1=\dfrac{90}{v-2} \)
\(\displaystyle t_2=\dfrac{90}{v+2} \)
\(\displaystyle \dfrac{90}{v-2}+\dfrac{90}{v+2}=24 \)
8.6.3.13. 8.6.3.15. 8.6.3.17.
8.6.3.19. 8.6.3.21. 8.6.3.23. Answer .
\(\dfrac{a^2-2a}{a^2+3a+2}\)
8.6.3.25.
8.6.3.27. Answer .
\(9x^2-7+\dfrac{4}{x^2}-\dfrac{1}{x^4} \)
8.6.3.29. Answer .
\(x^2-2x-2-\dfrac{1}{x-2}\)
8.6.3.31. 8.6.3.33. Answer .
\(\dfrac{3x+1}{2(x-3)(x+3)}\)
8.6.3.35. Answer .
\(\dfrac{2a^2-a+1}{(a-3)(a-1{})}\)
8.6.3.49. 8.6.3.51. 8.6.3.53.
9 Equations and Graphs 9.1 Properties of Lines 9.1.4 Problem Set 9.1
Warm Up 9.1.4.1. Answer .
\(A:\) negative;
\(B:\) negative;
\(C:\) positive;
\(D:\) zero
\(B\text{,}\) \(A\text{,}\) \(D\text{,}\) \(C\)
9.1.4.3. Answer .
Number
Negative
Their
\(\dfrac{2}{3} \) \(\dfrac{-3}{2} \) \(-1 \)
\(\dfrac{-5}{2} \) \(\dfrac{2}{5}\) \(-1\)
\(6 \) \(\dfrac{-1}{6} \) \(-1\)
\(-4\) \(\dfrac{1}{4} \) \(-1\)
\(-1 \) \(1\) \(-1\)
Skills Practice 9.1.4.5. Answer .
\(m\) is undefined; \((4,0)\)
9.1.4.11. Answer .
parallel: a, g, h; perpendicular: c, f
9.1.4.13. Answer .
68. The two lines meet at
\((20,68) \text{.}\)
Applications 9.1.4.15. Answer .
b.
\(m_{PQ}=\dfrac{-5}{2} \text{;}\) \(m_{PR}=\dfrac{2}{5} \)
9.1.4.17. Answer .
\(y=\dfrac{3}{2}x+\dfrac{5}{2}\text{;}\) the graph is below.
\(\displaystyle \dfrac{3}{2}\)
\(\displaystyle y=\dfrac{3}{2}x+\dfrac{7}{2}\)
9.1.4.19. Answer .
\(\displaystyle y=-2x-8\)
\(\displaystyle y=\dfrac{1}{2}x-3\)
9.1.4.21. Answer .
\(y=\dfrac{3}{2}x+\dfrac{15}{2}\)
9.2 The Distance and Midpoint Formulas 9.2.7 Problem Set 9.2
Warm Up 9.2.7.1. 9.2.7.3. Answer .
\(x\) \(-4\) \(-3\) \(-2\) \(-1\) \(0\) \(1\) \(2\) \(3\) \(4\)
\(y\) \(0\) \(\pm\sqrt{7}\) \(\pm\sqrt{12}\) \(\pm\sqrt{15}\) \(\pm 4\) \(\pm\sqrt{15}\) \(\pm\sqrt{12}\) \(\pm\sqrt{7}\) \(0\)
9.2.7.5. Answer .
\(\dfrac{5\pm \sqrt{33}}{2} \)
Skills Practice
9.2.7.7. Answer .
distance:
\(\sqrt{20} \text{;}\) midpoint:
\(\left(0,-2 \right) \)
9.2.7.9. Answer .
distance:
\(8\text{;}\) midpoint:
\(\left(-2,-1 \right) \)
9.2.7.11. Answer .
center:
\((0,0) \text{;}\) radius:
\(5 \)
9.2.7.13. Answer .
center:
\((-3,0) \text{;}\) radius:
\(\sqrt{10} \)
Applications 9.2.7.15. Answer .
\(15+\sqrt{80}+\sqrt{41} \approx 30.3\)
9.2.7.17. Answer .
\(\sqrt{50} \approx 7.1\)
9.2.7.19. Answer .
\(y=\dfrac{1}{2}x + \dfrac{5}{4}\)
9.2.7.21. Answer .
\(\displaystyle (220,-38.5)\)
Both distances are 165.8 mi.
9.2.7.23. 9.2.7.25. 9.2.7.27.
9.2.7.29. Answer .
\((x+4)^2+y^2=20 \text{;}\) center:
\((-4,0) \text{;}\) radius:
\(\sqrt{20} \)
9.2.7.31. Answer .
\(x^2+(y-5)^2=27 \text{;}\) center:
\((0,5) \text{;}\) radius:
\(\sqrt{27} \)
9.2.7.33. Answer .
\(\left(x-\dfrac{3}{2}\right)^2+(y+4)^2=\dfrac{29}{4}\)
9.2.7.35. Answer .
\(\left(x+3\right)^2+(y+1)^2=1\)
9.3 Conic Sections: Ellipses 9.3.5 Problem Set 9.3
Warm Up 9.3.5.1. Answer .
\(\displaystyle x^2+y^2=r^2\)
\(\displaystyle \dfrac{x^2}{r^2}+\dfrac{y^2}{r^2}=1\)
9.3.5.3. 9.3.5.5. Answer .
\(x\) -intercepts:
\((-6,0)\text{,}\) \((4,0)\text{,}\) vertex:
\(\left(-1,\dfrac{25}{2}\right)\)
Skills Practice
9.3.5.7. 9.3.5.9. 9.3.5.11. 9.3.5.13. Answer .
\(\displaystyle \dfrac{x^2}{9}+\dfrac{y^2}{4}=1\)
\(x\) \(0\) \(\pm 3\) \(-2\) \(\dfrac{\pm 3\sqrt{3} }{2} \)
\(y\) \(\pm 2\) \(0\) \(\dfrac{\pm 2\sqrt{5} }{2} \) \(1\)
9.3.5.15. Answer .
Radius 2
\(\displaystyle (-1,\pm \sqrt{3})\)
9.3.5.17. Answer .
\(\displaystyle a=\sqrt{3},~b=\sqrt{6}\)
None
9.3.5.19. Answer .
\((-1,4)\text{,}\) \((7,4)\text{,}\) \((3,1)\text{,}\) \((3,7)\) (Others are possible.)
9.3.5.21. Answer .
\(\displaystyle \dfrac{x^2}{4}+\dfrac{(y-2)^2}{9}=1\)
9.3.5.23. Answer .
\(\displaystyle \dfrac{(x-3)^2}{1}+\dfrac{(y+2)^2}{8}=1\)
9.3.5.25. Answer .
\(\dfrac{(x-1)^2}{9}+\dfrac{(y-6)^2}{4}=1\)
9.3.5.27. Answer .
\(\dfrac{(x-3)^2}{25}+\dfrac{(y-3)^2}{16}=1\)
Applications 9.3.5.29. Answer .
\(\displaystyle \dfrac{x^2}{10^2}+\dfrac{y^2}{7^2} = 1\)
4.2 ft
9.3.5.31. Answer .
\(\displaystyle \dfrac{x^2}{24^2}+\dfrac{y^2}{8^2} = 1\)
10.29 ft
9.4 Conic Sections: Hyperbolas 9.4.6 Problem Set 9.4
Skills Practice
9.4.6.3. 9.4.6.5. 9.4.6.7. 9.4.6.9. Answer .
\(\displaystyle \dfrac{x^2}{9} - \dfrac{y^2}{3} =1\)
\(x\) \(0\) \(\dfrac{\pm3\sqrt{5}}{2} \) \(5\) \(\dfrac{\pm 15}{4} \)
\(y\) undefined
\(\pm 2\) \(\dfrac{\pm 16}{3} \) \(-3\)
9.4.6.11.
9.4.6.13. Answer .
\(\left(-2, -2\pm \sqrt{6} \right) \text{,}\) \(\left(-2 \pm \sqrt{5} ,1\right) \)
9.4.6.15. Answer .
\(\left(1 -4\pm 2\sqrt{2} \right) \text{,}\) \((-2,-8) \text{,}\) \((4,-8)\)
9.4.6.17. Answer .
\(\left(3 \pm \sqrt{5} \right) \text{,}\) \(\left(3 \pm 2\sqrt{2}, 3 \right)\)
9.4.6.19. Answer .
\(16x^2-y^2-192x-4y+556=0\)
9.4.6.21. Answer .
\(x^2-4y^2+10x-16y-27=0\)
9.4.6.23. Answer .
Parabola; vertex
\((0,2)\text{,}\) opens downward,
\(a=\dfrac{-1}{2} \)
9.4.6.25. Answer .
Hyperbola; center
\(\left(\dfrac{-1}{8},-1 \right) \text{,}\) transverse axis vertical,
\(a^2=\dfrac{15}{65} \text{,}\) \(b^2=\dfrac{15}{16} \)
9.4.6.27. Answer .
Parabola; vertex
\((-4,2)\text{,}\) opens upward,
\(a=\dfrac{1}{4} \)
Applications
9.5 Nonlinear Systems 9.5.4 Problem Set 9.5
Warm Up 9.5.4.1. 9.5.4.3. Skills Practice
9.5.4.5. 9.5.4.7. 9.5.4.9.
9.5.4.11. Answer .
\((2,2) \text{,}\) \((-2,-2) \)
9.5.4.13. Answer .
\((2,-1) \text{,}\) \((-2,1) \text{,}\) \((1,-2) \text{,}\) \((-1,2) \)
9.5.4.15. 9.5.4.17. 9.5.4.19. Answer .
\((0,4) \text{,}\) \((-2,0) \)
Applications
9.5.4.21. 9.5.4.23. Answer .
\(P=6\) lb per sq in;
\(V=5\) cu. in.
9.5.4.25. Answer .
harvst 1800; stable population 3000
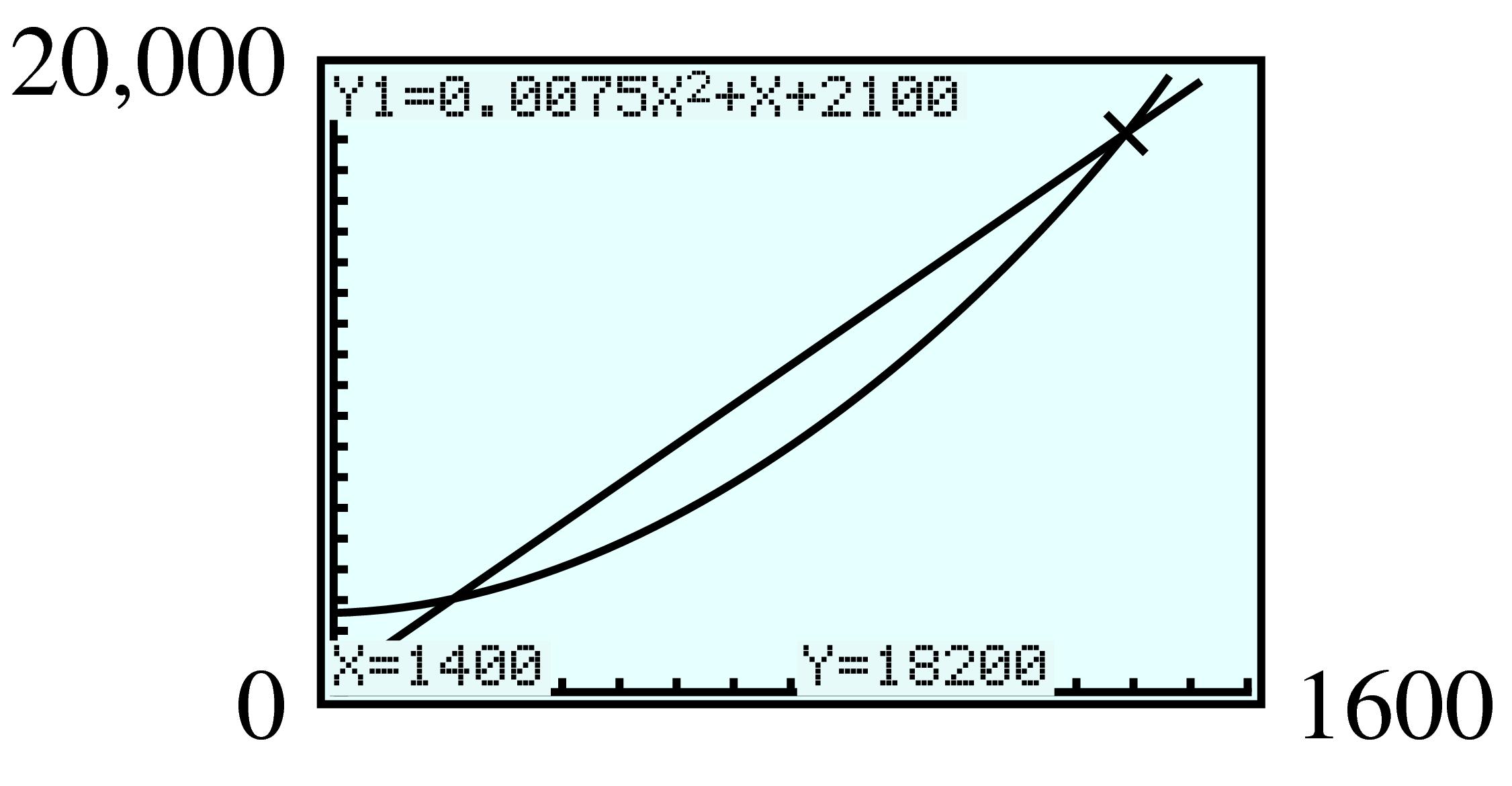
9.5.4.27. Answer .
\(\displaystyle (200,~ 2600), (1400,~ 18,200)\)
9.6 Chapter 9 Summary and Review 9.6.3 Chapter 9 Review Problems
9.6.3.3. Answer .
\(y=\dfrac{-2}{3}x+\dfrac{14}{3} \)
9.6.3.4. Answer .
\(y=\dfrac{3}{2}x+\dfrac{5}{2} \)
9.6.3.5. Answer .
\(y=\dfrac{2}{3}x-\dfrac{26}{3} \)
9.6.3.6. 9.6.3.7. 9.6.3.8.
9.6.3.9. 9.6.3.10. 9.6.3.11. 9.6.3.12. 9.6.3.13. 9.6.3.14. 9.6.3.15. 9.6.3.16. 9.6.3.17. 9.6.3.18.
9.6.3.19. Answer .
\(\displaystyle (x-2)^2+(y+1)^2=9\)
Circle: center
\((2,-1)\text{,}\) radius 3
9.6.3.20. Answer .
\(\displaystyle x^2+(y-3)^2=13\)
Circle: center
\((0,3)\text{,}\) radius
\(\sqrt{13}\)
9.6.3.21. Answer .
\(\displaystyle \dfrac{(x-2)^2}{4}+\dfrac{(y+2)^2}{16}=1\)
Ellipse: center
\((2,-2)\text{,}\) \(a=2\text{,}\) \(b=4\)
9.6.3.22. Answer .
\(\displaystyle \dfrac{(x+1)^2}{5}+\dfrac{(y-2)^2}{8}=1\)
Ellipse: center
\((-1,2)\text{,}\) \(a=\sqrt{5}\text{,}\) \(b=\sqrt{8}\)
9.6.3.23. Answer .
\(\displaystyle y+10=(x-4)^2\)
Parabola: vertex
\((4,10)\text{,}\) opens upward,
\(a=1\)
9.6.3.24. Answer .
\(\displaystyle x-2=\dfrac{-1}{4}(y+3)^2\)
Parabola: vertex
\((2,-3)\text{,}\) opens left,
\(a=\dfrac{-1}{4}\)
9.6.3.25. Answer .
\(\displaystyle y+2=-(x-2)^2\)
Parabola: vertex
\((2,-2)\text{,}\) opens downward,
\(a=-1\)
9.6.3.26. Answer .
\(\displaystyle x+\dfrac{3}{2}=\dfrac{1}{2}(y-1)^2\)
Parabola: vertex
\(\left(\dfrac{-3}{2},1\right)\text{,}\) opens right,
\(a=\dfrac{1}{2}\)
9.6.3.27. Answer .
\(\displaystyle \dfrac{(y-4)^2}{6}-\dfrac{(x+2)^2}{4}=1\)
Hyperbola: center
\((-2,4)\text{,}\) transverse axis vertical,
\(a=2\text{,}\) \(b=\sqrt{6}\)
9.6.3.28. Answer .
\(\displaystyle \dfrac{(x-4)^2}{4}-\dfrac{(y+3)^2}{9}=1\)
Hyperbola: center
\((4,-3)\text{,}\) transverse axis horizontal,
\(a=2\text{,}\) \(b=3\)
9.6.3.29. Answer .
\(\displaystyle \dfrac{x^2}{5}-\dfrac{(y-3)^2}{10}=1\)
Hyperbola: center
\((0,3)\text{,}\) transverse axis horizontal,
\(a=\sqrt{5}\text{,}\) \(b=\sqrt{10}\)
9.6.3.30. Answer .
\(\displaystyle \dfrac{y^2}{3}-\dfrac{(x-4)^2}{12}=1\)
Hyperbola: center
\((4,0)\text{,}\) transverse axis vertical,
\(a=2\sqrt{3}\text{,}\) \(b=\sqrt{310}\)
9.6.3.31. Answer .
\(\displaystyle \dfrac{x^2}{25}+\dfrac{y^2}{64}=1\)
\(\displaystyle \dfrac{\pm 24}{5}\)
9.6.3.32. Answer .
\(\displaystyle \dfrac{x^2}{169}+\dfrac{y^2}{81}=1\)
\(\displaystyle \dfrac{\pm 45}{13}\)
9.6.3.33. 9.6.3.34. 9.6.3.35. Answer .
\(\dfrac{(x+1)^2}{16}+\dfrac{(y-4)^2}{4}=1 \)
9.6.3.36. Answer .
\(\dfrac{(x-3)^2}{4}+\dfrac{(y-1)^2}{25}=1 \)
9.6.3.37. Answer .
\(\dfrac{(x-2)^2}{16}-\dfrac{(y+3)^2}{9}=1 \)
9.6.3.38. Answer .
\((x+3)^2 -\dfrac{(y-1)^2}{9}=1 \)
9.6.3.39. 9.6.3.40. Answer .
\((\pm\sqrt{3}, \pm 4) \)
9.6.3.41. Answer .
\((1,-2) \text{,}\) \((-1,2) \text{,}\) \(\left(2\sqrt{3}, \dfrac{-1}{\sqrt{3}} \right) \text{,}\) \(\left(-2\sqrt{3}, \dfrac{1}{\sqrt{3}} \right) \)
9.6.3.42. Answer .
\(\left(\dfrac{\sqrt{34}}{2}, \dfrac{\sqrt{34}}{2} \right) \text{,}\) \(\left(\dfrac{-\sqrt{34}}{2}, \dfrac{-\sqrt{34}}{2} \right) \)
9.6.3.43. Answer .
Moia: 45 mph, Fran: 50 mph
9.6.3.44. 9.6.3.45. 9.6.3.46. 9.6.3.47. Answer .
Morning train: 20 mph, evening train: 30 mph
9.6.3.48.
10 Logarithmic Functions 10.1 Logarithmic Functions 10.1.7 Problem Set 10.1
Warm Up
10.1.7.5. Answer .
\(\log_b{\left(\dfrac{1}{4}\right)}\)
10.1.7.7. Answer .
\(\log_{10}{\left(\sqrt{\dfrac{xy}{z^3}}\right)}\)
Skills Practice 10.1.7.11. Answer .
\(\displaystyle 15.6144\)
\(\displaystyle 0.4186\)
10.1.7.15. Answer .
\(\displaystyle 25.70\)
\(\displaystyle 3.31\)
10.1.7.17. Answer .
\(\displaystyle \dfrac{1}{2}\)
\(\displaystyle 01\)
10.1.7.19. Answer .
81
4
1.8
\(\displaystyle a\)
10.1.7.21. 10.1.7.23. Applications 10.1.7.29. Answer .
The graph resembles a logarithmic function. The function is close to the points but appears too steep at first and not steep enough after
\(n = 15\text{.}\) Overall, it is a good fit.
\(f\) grows (more and more slowly) without bound.
\(f\) will eventually exceed
\(100\) per cent, but no one can forget more than 100% of what is learned.
10.1.7.31.
10.2 Logarithmic Scales 10.2.7 Problem Set 10.2
Warm Up 10.2.7.1. Answer .
0 and 1
2 and 3
\(-1\) and 0
6 and 7
10.2.7.3. Answer .
3981.1
5.01
0.00079
0.398
Skills Practice 10.2.7.5. 10.2.7.7. 10.2.7.9. Answer .
\(1.58\text{,}\) \(6.31\text{,}\) \(15.8\text{,}\) \(63.1\)
10.2.7.11. 10.2.7.13. 10.2.7.15. 10.2.7.17. Answer .
6,309,573 watts per square meter
Applications 10.2.7.19. Answer .
\(1\text{,}\) \(80\text{,}\) \(330\text{,}\) \(1600\text{,}\) \(7000\text{,}\) \(4\times 10^7\)
10.2.7.21. Answer .
Proxima Centauri:
\(15.5\text{;}\) Barnard:
\(13.2\text{;}\) Sirius:
\(1.4\text{;}\) Vega:
\(0.6\text{;}\) Arcturus:
\(-0.4\text{;}\) Antares:
\(-4.7\text{;}\) Betelgeuse:
\(-7.2\)
10.2.7.23. 10.2.7.25. Answer .
\(10^{3.4} \approx 2512\)
10.2.7.27. Answer .
A:
\(a\approx 45\text{,}\) \(p \approx 7.4\%\text{;}\) B:
\(a \approx 400\text{,}\) \(p \approx 15\%\text{;}\) C:
\(a\approx 6000\text{,}\) \(p\approx 50\%\text{;}\) D:
\(a \approx 13000\text{,}\) \(p \approx 45\%\)
10.2.7.29. 10.2.7.32. 10.2.7.33.
10.3 The Natural Base 10.3.7 Homework 10.3
Skills Practice
10.3.7.1. Answer .
\(x\) \(-10\) \(-5\) \(0\) \(5\) \(10\) \(15\) \(20\)
\(f(x)\) \(0.135\) \(0.368\) \(1\) \(2.718\) \(7.389\) \(20.086\) \(54.598\)
10.3.7.3. Answer .
\(x\) \(-10\) \(-5\) \(0\) \(5\) \(10\) \(15\) \(20\)
\(f(x)\) \(20.086\) \(4.482\) \(1\) \(0.223\) \(0.05\) \(0.011\) \(0.00248\)
10.3.7.5. Answer .
\(\displaystyle \dfrac{1}{x} \)
\(\displaystyle \dfrac{1}{2} \)
10.3.7.11. Answer .
\(P (t) = 20\left(e^{0.4} \right)^t \approx 20\cdot 1.492^t\text{;}\) increasing; initial value
\(20\)
10.3.7.13. Answer .
\(P (t) = 6500\left(e^{-2.5} \right)^t \approx 6500\cdot 0.082^t\text{;}\) decreasing; initial value
\(6500\)
10.3.7.15. Answer .
\(x\) \(0\) \(0.5\) \(1\) \(1.5\) \(2\) \(2.5\)
\(e^x\) \(1 \) \(1.6487\) \(2.7183\) \(4.4817\) \(7.3891\) \(12.1825\)
Each ratio is
\(e^{0.5} \approx 1.6487\text{:}\) Increasing
\(x\) -values by a constant
\(\Delta x = 0.5\) corresponds to multiplying the
\(y\) -values of the exponential function by a constant factor of
\(e^{\Delta x}\text{.}\)
10.3.7.17. Answer .
\(x\) \(0\) \(0.6931\) \(1.3863\) \(2.0794\) \(2.7726\) \(3.4657\) \(4.1589\)
\(e^x\) \(1 \) \(2\) \(4\) \(8\) \(16\) \(32\) \(64\)
Each difference in
\(x\) -values is approximately
\(\ln 2\approx 0.6931\text{:}\) Increasing
\(x\) -values by a constant
\(\Delta x = \ln 2\) corresponds to multiplying the
\(y\) -values of the exponential function by a constant factor of
\(e^{\Delta x} = e^{\ln 2} = 2\text{.}\) That is, each function value is approximately equal to double the previous one.
10.3.7.19. 10.3.7.21. 10.3.7.23. 10.3.7.25.
10.3.7.27. Answer .
\(t=\dfrac{1}{k}\ln {(y)} \)
10.3.7.29. Answer .
\(t=\ln {\left(\dfrac{k}{k-y}\right)} \)
10.3.7.31. 10.3.7.33. Answer .
\(n\) \(0.39\) \(3.9\) \(39\) \(390\)
\(\ln {(n)}\) \(-0.942 \) \(1.361 \) \(3.664 \) \(5.966 \)
Each difference in function values is approximately
\(\ln 10\approx 2.303\text{:}\) Multiplying
\(x\) -values by a constant factor of 10 corresponds to adding a constant value of
\(\ln 10\) to the
\(y\) -values of the natural log function.
10.3.7.35. Answer .
\(n\) \(2\) \(4\) \(8\) \(16\)
\(\ln n\) \(0.693 \) \(1.386 \) \(2.079 \) \(2.773 \)
Each quotient equals
\(k\text{,}\) where
\(n = 2^k\text{.}\) Because
\(\ln {(n)} = \ln {(2^k)} = k\cdot \ln {(2)}\text{,}\) \(k = \dfrac{\ln {(n)}}{\ln {(2)}}\text{.}\)
10.3.7.37. Answer .
\(\displaystyle N (t) = 100e^{(\ln {(2)})t}\approx 100e^{0.6931t}\)
10.3.7.39. Answer .
\(\displaystyle N (t) = 1200e^{(\ln {(0.6)})t}\approx 1200e^{-0.5108t}\)
10.3.7.41. Answer .
\(\displaystyle N (t) = 10e^{(\ln {(1.15)})t}\approx 10e^{0.1398t}\)
Applications 10.3.7.43. Answer .
\(\displaystyle N(t)=6000e^{0.04t} \)
\(t\) \(0\) \(5\) \(10\) \(15\) \(20\) \(25\) \(30\)
\(N(t)\) \(6000\) \(7328\) \(8951\) \(10,933\) \(13,353\) \(16,310\) \(19,921\)
10.3.7.45. 10.3.7.47. Answer .
\(\displaystyle \left(\dfrac{35,000}{20,000} \right)^{1/10}\approx e^{0.056} \)
\(\displaystyle P(t) = 20,000e^{0.056t} \)
10.3.7.49. Answer .
\(\displaystyle \left(\dfrac{385}{500} \right)^{1/2}\approx e^{-0.1307} \)
\(\displaystyle N(t) = 500e^{-0.1307t} \)
10.3.7.51. Answer .
\(\displaystyle A(t) = 500e^{0.095t}\)
d–e
10.3.7.53. 10.3.7.55. Answer .
\(\frac{1}{2}N_0 \text{,}\) \(\frac{1}{4}N_0 \text{,}\) \(\frac{1}{16}N_0\)
\(\displaystyle N (t) = N_0e^{-0.0866t}\)
10.3.7.57. Answer .
\(\displaystyle y = 116 (0.975)^t\)
\(\displaystyle y = 116 (0.975)^t\)
\(\displaystyle G (t) = 116e^{-0.025t}\)
10.4 Chapter 10 Summary and Review 10.4.3 Chapter 10 Review Problems
10.4.3.5. 10.4.3.7. 10.4.3.9. 10.4.3.11.
10.4.3.17. 10.4.3.19. 10.4.3.21. 10.4.3.27. Answer .
\(\displaystyle P = 7,894,862e^{-0.011t}\)
10.4.3.29. Answer .
\(\displaystyle t = 20 \ln\left(\dfrac{A}{1000} \right)\)
10.4.3.31. Answer .
\(t=\dfrac{-1}{k}\ln{\left(\dfrac{y-6}{12} \right)} \)
10.4.3.33. 10.4.3.35. Answer .
\(P(t) = 750 (1.3771)^t\)
10.4.3.37. Answer .
\(N(t) = 600 e^{-0.9163t}\)
10.4.3.39. 10.4.3.41. Answer .
Order 3: 17,000; Order 4: 5000; Order 8: 40; Order 9: 11