Before you keep reading...

Runestone Academy can only continue if we get support from individuals like you. As a student you are well aware of the high cost of textbooks. Our mission is to provide great books to you for free, but we ask that you consider a $10 donation, more if you can or less if $10 is a burden.

Support Runestone Academy Today

5.10. The Shell Sort

The Shell sort, sometimes called the diminishing increment sort, improves on the insertion sort by breaking the original list into a number of smaller sublists, each of which is sorted using an insertion sort. The unique way that these sublists are chosen is the key to the Shell sort. Instead of breaking the list into sublists of contiguous items, the Shell sort uses an increment $i$, sometimes called the gap, to create a sublist by choosing all items that are $i$ items apart.

This can be seen in Figure 6. This list has nine items. If we use an increment of three, there are three sublists, each of which can be sorted by an insertion sort. After completing these sorts, we get the list shown in Figure 7. Although the list shown in Figure 7 is not completely sorted, something very interesting has happened. By sorting the sublists, we have moved the items closer to where they actually belong.

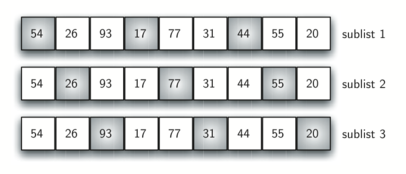
Figure 6: A Shell Sort with Increments of Three

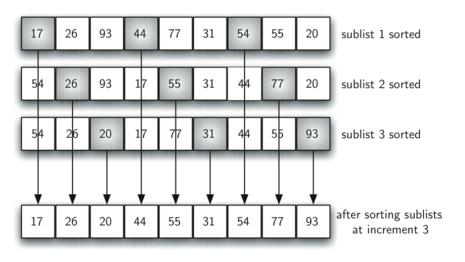
Figure 7: A Shell Sort after Sorting Each Sublist

Figure 8 shows a final insertion sort using an increment of one—in other words, a standard insertion sort. Note that by performing the earlier sublist sorts, we have now reduced the total number of shifting operations necessary to put the list in its final order. For this case, we need only four more shifts to complete the process.

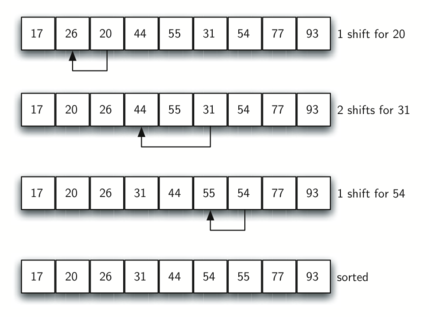
Figure 8: ShellSort: A Final Insertion Sort with Increment of 1

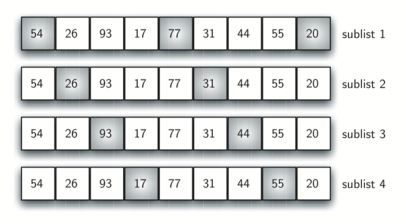
Figure 9: Initial Sublists for a Shell Sort

We said earlier that the way in which the increments are chosen is the unique feature of the Shell sort. The function shown in ActiveCode 1 uses a different set of increments. In this case, we begin with $\frac{n}{2}$ sublists. On the next pass, $\frac{n}{4}$ sublists are sorted. Eventually, a single list is sorted with the basic insertion sort. Figure 9 shows the first sublists for our example using this increment.

The following invocation of the shell_sort function shows the partially sorted lists after each increment, with the final sort being an insertion sort with an increment of one.

def shell_sort(a_list): sublist_count = len(a_list) // 2 while sublist_count > 0: for pos_start in range(sublist_count): gap_insertion_sort(a_list, pos_start, sublist_count) print("After increments of size", sublist_count, "the list is", a_list) sublist_count = sublist_count // 2 def gap_insertion_sort(a_list, start, gap): for i in range(start + gap, len(a_list), gap): cur_val = a_list[i] cur_pos = i while cur_pos >= gap and a_list[cur_pos - gap] > cur_val: a_list[cur_pos] = a_list[cur_pos - gap] cur_pos = cur_pos - gap a_list[cur_pos] = cur_val a_list = [54, 26, 93, 17, 77, 31, 44, 55, 20] shell_sort(a_list) print(a_list)

Before you keep reading...

Making great stuff takes time and $$. If you appreciate the book you are reading now and want to keep quality materials free for other students please consider a donation to Runestone Academy. We ask that you consider a $10 donation, but if you can give more thats great, if $10 is too much for your budget we would be happy with whatever you can afford as a show of support.

Support Runestone Academy Today

Initialize Run Stop
Beginning Step Forward Step Backward End

At first glance you may think that a Shell sort cannot be better than an insertion sort since it does a complete insertion sort as the last step. It turns out, however, that this final insertion sort does not need to do very many comparisons (or shifts) since the list has been presorted by earlier incremental insertion sorts, as described above. In other words, each pass produces a list that is “more sorted” than the previous one. This makes the final pass very efficient.

Although a general analysis of the Shell sort is well beyond the scope of this text, we can say that it tends to fall somewhere between $O(n)$ and $O(n^2)$, based on the behavior described above. For the increments shown in Listing 5, the performance is $O(n^2)$. By changing the increment, for example using $2^k-1$ (1, 3, 7, 15, 31, and so on), a Shell sort can perform at $O(n^{\frac{3}{2}})$.

Self Check

Q-3: Given the following list of numbers: [5, 16, 20, 12, 3, 8, 9, 17, 19, 7] Which answer illustrates the contents of the list after all swapping is complete for a gap size of 3?

• [5, 3, 8, 7, 16, 19, 9, 17, 20, 12]
• Each group of numbers represented by index positions 3 apart are sorted correctly.
• [3, 7, 5, 8, 9, 12, 19, 16, 20, 17]
• This solution is for a gap size of two.
• [3, 5, 7, 8, 9, 12, 16, 17, 19, 20]
• This is list completely sorted, you have gone too far.
• [5, 16, 20, 3, 8, 12, 9, 17, 20, 7]
• The gap size of three indicates that the group represented by every third number e.g. 0, 3, 6, 9 and 1, 4, 7 and 2, 5, 8 are sorted not groups of 3.

You have attempted 1 of 3 activities on this page