5.4. The Binary Search

It is possible to take greater advantage of the ordered list if we are clever with our comparisons. In the sequential search, when we compare against the first item, there are at most $n-1$ more items to look through if the first item is not what we are looking for. Instead of searching the list in sequence, a binary search will start by examining the middle item. If that item is the one we are searching for, we are done. If it is not the correct item, we can use the ordered nature of the list to eliminate half of the remaining items. If the item we are searching for is greater than the middle item, we know that the entire first (left) half of the list as well as the middle item can be eliminated from further consideration. The item, if it is in the list, must be in the second (right) half.

We can then repeat the process with the left half. Start at the middle item and compare it against what we are looking for. Again, we either find it or split the list in half, therefore eliminating another large part of our possible search space. Figure 3 shows how this algorithm can quickly find the value 54. The complete function is shown in CodeLens 3.

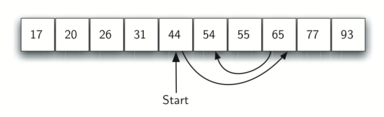
Figure 3: Binary Search of an Ordered List of Integers

Activity: CodeLens Binary Search of an Ordered List (search3)

Before we move on to the analysis, we should note that this algorithm is a great example of a divide and conquer strategy. Divide and conquer means that we divide the problem into smaller pieces, solve the smaller pieces in some way, and then reassemble the whole problem to get the result. When we perform a binary search of a list, we first check the middle item. If the item we are searching for is less than the middle item, we can simply perform a binary search of the left half of the original list. Likewise, if the item is greater, we can perform a binary search of the right half. Either way, this is a recursive call to the binary search function passing a smaller list. CodeLens 4 shows this recursive version.

Activity: CodeLens A Binary Search--Recursive Version (search4)

5.4.1. Analysis of Binary Search

To analyze the binary search algorithm, we need to recall that each comparison eliminates about half of the remaining items from consideration. What is the maximum number of comparisons this algorithm will require to check the entire list? If we start with $n$ items, about $\frac{n}{2}$ items will be left after the first comparison. After the second comparison, there will be about $\frac{n}{4}$. Then $\frac{n}{8}$, $\frac{n}{16}$, and so on. How many times can we split the list? Table 3 helps us to see the answer.

Table 3: Tabular Analysis for a Binary Search

Comparisons	Approximate Number of Items Left
1	$\frac{n}{2}$
2	$\frac{n}{4}$
3	$\frac{n}{8}$
…
$i$	$\frac{n}{2^i}$

When we split the list enough times, we end up with a list that has just one item. Either that is the item we are looking for or it is not. Either way, we are done. The number of comparisons necessary to get to this point is $i$ where $\frac{n}{2^i}=1$. Solving for $i$ gives us $i=\log n$. The maximum number of comparisons is logarithmic with respect to the number of items in the list. Therefore, the binary search is $O(\log n)$.

One additional analysis issue needs to be addressed. In the recursive solution shown above, the recursive call

binary_search_rec(a_list[:midpoint], item)

uses slicing operator to create the left half of the list that is then passed to the next invocation (similarly for the right half as well). The analysis that we did above assumed that slicing takes constant time. However, we know that in Python it is actually $O(k)$. This means that the binary search using slicing will not perform in strict logarithmic time. Luckily this can be remedied by passing the list along with the starting and ending indices. The indices can be calculated as we did in Listing 3. We leave this implementation as an exercise.

Even though a binary search is generally better than a sequential search, it is important to note that for small values of $n$, the additional cost of sorting is probably not worth it. In fact, we should always consider whether it is cost effective to take on the extra work of sorting to gain searching benefits. If we can sort once and then search many times, the cost of the sort is not so significant. However, for large lists, sorting even once can be so expensive that simply performing a sequential search from the start may be the best choice.

Self Check

Q-3: Suppose you have the following sorted list [3, 5, 6, 8, 11, 12, 14, 15, 17, 18] and are using the recursive binary search algorithm. Which group of numbers correctly shows the sequence of comparisons used to find the key 8.

• 11, 5, 6, 8
• Looks like you might be guilty of an off-by-one error. Remember the first position is index 0.
• 12, 6, 11, 8
• Binary search starts at the midpoint and halves the list each time.
• 3, 5, 6, 8
• Binary search does not start at the beginning and search sequentially, its starts in the middle and halves the list after each compare.
• 18, 12, 6, 8
• It appears that you are starting from the end and halving the list each time.

Q-4: Suppose you have the following sorted list [3, 5, 6, 8, 11, 12, 14, 15, 17, 18] and are using the recursive binary search algorithm. Which group of numbers correctly shows the sequence of comparisons used to search for the key 16?

• 11, 14, 17
• Looks like you might be guilty of an off-by-one error. Remember the first position is index 0.
• 18, 17, 15
• Remember binary search starts in the middle and halves the list.
• 14, 17, 15
• Looks like you might be off by one, be careful that you are calculating the midpont using integer arithmetic.
• 12, 17, 15
• Binary search starts at the midpoint and halves the list each time. It is done when the list is empty.

You have attempted 1 of 4 activities on this page