3.21. Implementación de una lista no ordenada: Listas enlazadas¶
Con el fin de implementar una lista no ordenada, vamos a construir lo que comúnmente se conoce como una lista enlazada (encadenada o ligada). Recordemos que tenemos que estar seguros de que podemos mantener el posicionamiento relativo de los ítems. Sin embargo, no existe ningún requisito que mantenga ese posicionamiento en memoria contigua. Por ejemplo, considere la colección de elementos mostrados en la Figura 1. Parece que estos valores se han colocado al azar. Si podemos mantener alguna información explícita en cada ítem, es decir, la ubicación del ítem siguiente (véase la Figura 2), entonces la posición relativa de cada ítem puede expresarse simplemente siguiendo el enlace de un ítem al siguiente.

Figura 1: Ítems no restringidos en su ubicación física¶
Figura 1: Ítems no restringidos en su ubicación física
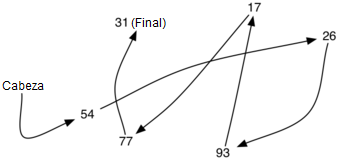
Figura 2: Posiciones relativas mantenidas por enlaces explícitos¶
Figura 2: Posiciones relativas mantenidas por enlaces explícitos
Es importante tener en cuenta que la ubicación del primer ítem de la lista debe especificarse explícitamente. Una vez que sepamos dónde está el primer ítem, éste puede decirnos dónde está el segundo, y así sucesivamente. La referencia externa se conoce a menudo como la cabeza de la lista. Del mismo modo, el último ítem necesita saber que no hay ningún ítem siguiente.
3.21.1. La clase Nodo¶
El bloque constructivo básico para la implementación de la lista enlazada es el nodo. Cada objeto nodo debe contener al menos dos piezas de información. En primer lugar, el nodo debe contener el ítem de lista en sí mismo. Esto lo llamaremos el campo de dato del nodo. Además, cada nodo debe contener una referencia al siguiente nodo. El Programa 1 muestra la implementación en Python. Para construir un nodo, usted debe proporcionar el valor inicial del dato del nodo. La evaluación de la instrucción de asignación que aparece más abajo producirá un objeto nodo que contiene el valor 93 (véase la Figura 3). Tenga en cuenta que típicamente representaremos un objeto nodo como se muestra en la Figura 4. La clase Nodo también incluye los métodos habituales para acceder y modificar el dato y la siguiente referencia.
Programa 1
class Nodo:
def __init__(self,datoInicial):
self.dato = datoInicial
self.siguiente = None
def obtenerDato(self):
return self.dato
def obtenerSiguiente(self):
return self.siguiente
def asignarDato(self,nuevodato):
self.dato = nuevodato
def asignarSiguiente(self,nuevosiguiente):
self.siguiente = nuevosiguiente
Creamos objetos Nodo de la manera habitual.
>>> temp = Nodo(93)
>>> temp.obtenerDato()
93
El valor de referencia especial de Python None desempeñará un papel importante en la clase Nodo y más tarde en la propia lista enlazada. Una referencia a None indicará el hecho de que no hay nodo siguiente. Fíjese en el constructor que un nodo se crea inicialmente con siguiente asignado a None. Puesto que esto a veces se denomina “puesta a tierra del nodo”, usaremos el símbolo estándar de tierra para designar una referencia que se refiere a None. Siempre es una buena idea asignar explícitamente None a los valores de referencia iniciales siguientes.
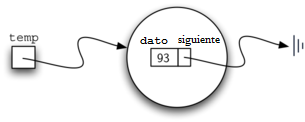
Figura 3: Un objeto de nodo contiene el ítem y una referencia al siguiente nodo¶
Figura 3: Un objeto de nodo contiene el ítem y una referencia al siguiente nodo
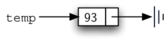
Figura 4: Representación típica para un nodo¶
Figura 4: Representación típica para un nodo
3.21.2. La clase ListaNoOrdenada¶
Como sugerimos anteriormente, la lista no ordenada se construirá a partir de una colección de nodos, cada uno vinculado al siguiente mediante referencias explícitas. Siempre y cuando sepamos dónde encontrar el primer nodo (que contiene el primer ítem), cada ítem posterior se puede encontrar sucesivamente siguiendo los enlaces subsiguientes. Con esto en mente, la clase ListaNoOrdenada debe mantener una referencia al primer nodo. El Programa 2 muestra el constructor. Tenga en cuenta que cada objeto de la lista mantendrá una sola referencia a la cabeza de la lista.
Programa 2
class ListaNoOrdenada:
def __init__(self):
self.cabeza = None
Inicialmente, cuando construimos una lista, no hay ítems. La instrucción de asignación
>>> milista = ListaNoOrdenada()
crea la representación de lista enlazada que se muestra en la Figura 5. Como hemos comentado en el apartado sobre la clase Nodo, la referencia especial None será utilizada nuevamente para indicar que la cabeza de la lista no se refiere a nada. Eventualmente, la lista de ejemplo dada anteriormente será representada por una lista enlazada como se muestra en la Figura 6. La cabeza de la lista se refiere al primer nodo que contiene el primer ítem de la lista. A su vez, ese nodo contiene una referencia al siguiente nodo (el siguiente ítem) y así sucesivamente. Es muy importante tener en cuenta que la clase lista en sí misma no contiene ningún objeto nodo. Contiene, en cambio, una sola referencia únicamente al primer nodo de la estructura enlazada.
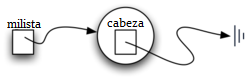
Figura 5: Una lista vacía¶
Figura 5: Una lista vacía
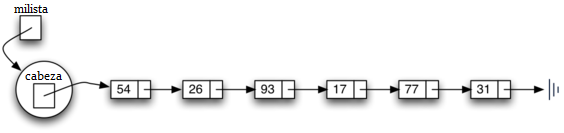
Figura 6: Una lista enlazada de enteros¶
Figura 6: Una lista enlazada de enteros
El método estaVacia, que se muestra en el Programa 3, simplemente comprueba si la cabeza de la lista es una referencia a None. El resultado de la expresión booleana self.cabeza == None sólo será verdadero si no hay nodos en la lista enlazada. Dado que una lista nueva está vacía, el constructor y la comprobación de estar vacía deben ser coherentes entre sí. Esto muestra la ventaja de usar la referencia None para denotar el “final” de la estructura enlazada. En Python, None puede compararse con cualquier referencia. Dos referencias son iguales si ambas se refieren al mismo objeto. Usaremos esto con frecuencia en nuestros métodos restantes.
Programa 3
def estaVacia(self):
return self.cabeza == None
Entonces, ¿cómo incluiremos ítems en nuestra lista? Tenemos que implementar el método agregar. Sin embargo, antes de que podamos hacer eso, necesitamos enfrentar la importante cuestión de dónde ubicar el nuevo ítem en la lista enlazada. Dado que esta lista no está ordenada, no es importante la ubicación específica del nuevo ítem con respecto a los otros elementos que ya están en la lista. El nuevo ítem puede ubicarse en cualquier parte. Con esto en mente, tiene sentido poner el nuevo ítem en la ubicación más fácil posible.
Recuerde que la estructura de lista enlazada nos proporciona sólo un punto de entrada, la cabeza de la lista. Todos los demás nodos sólo pueden ser alcanzados accediendo al primer nodo y luego siguiendo los enlaces subsiguientes. Esto significa que el lugar más fácil para agregar el nuevo nodo está justo en la cabeza, o al principio, de la lista. En otras palabras, haremos que el nuevo ítem sea el primer ítem de la lista y los elementos existentes tendrán que enlazarse a este nuevo primer ítem de modo que estarán a continuación de él.
La lista enlazada mostrada en la Figura 6 fue construida llamando al método agregar varias veces.
>>> milista.agregar(31)
>>> milista.agregar(77)
>>> milista.agregar(17)
>>> milista.agregar(93)
>>> milista.agregar(26)
>>> milista.agregar(54)
Note que, como 31 es el primer ítem agregado a la lista, eventualmente será el último nodo en la lista enlazada ya que cada uno de los otros ítems es agregado adelante de él. Además, puesto que 54 es el último ítem añadido, se convertirá en el dato del primer nodo de la lista enlazada.
El método agregar se muestra en el Programa 4. Cada ítem de la lista debe residir en un objeto nodo. La línea 2 crea un nuevo nodo y hace que el ítem sea su dato. Ahora debemos completar el proceso uniendo el nuevo nodo a la estructura existente. Esto requiere dos pasos como se muestra en la Figura 7. El paso 1 (línea 3) cambia la referencia siguiente del nuevo nodo para que se refiera al primer nodo antiguo de la lista. Ahora que el resto de la lista ha sido correctamente adjuntado al nuevo nodo, podemos modificar la cabeza de la lista para hacer referencia al nuevo nodo. La instrucción de asignación en la línea 4 asigna la cabeza de la lista.
El orden de los dos pasos descritos anteriormente es muy importante. ¿Qué sucede si se invierte el orden de las líneas 3 y 4? Si la modificación de la cabeza de la lista ocurre primero, el resultado se puede ver en la Figura 8. Dado que la cabeza era la única referencia externa a los nodos de lista, todos los nodos originales se pierden y ya no se puede acceder.
Programa 4
def agregar(self,item):
temp = Nodo(item)
temp.asignarSiguiente(self.cabeza)
self.cabeza = temp
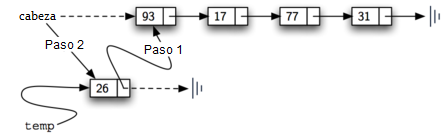
Figura 7: Agregar un nuevo nodo es un proceso de dos pasos¶
Figura 7: Agregar un nuevo nodo es un proceso de dos pasos
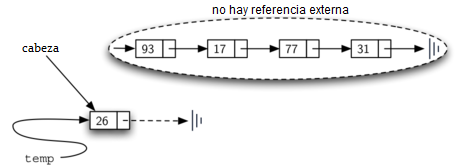
Figura 8: Resultado de invertir el orden de los dos pasos¶
Figura 8: Resultado de invertir el orden de los dos pasos
Los siguientes métodos que implementaremos–tamano, buscar y remover–están basados en una técnica conocida como recorrido de listas enlazadas. Recorrido se refiere al proceso de visitar sistemáticamente cada nodo. Para ello utilizamos una referencia externa que comienza en el primer nodo de la lista. A medida que visitamos cada nodo, movemos la referencia al siguiente nodo “recorriendo” la siguiente referencia.
Para implementar el método tamano, necesitamos recorrer la lista enlazada y mantener un recuento del número de nodos que aparecieron. El Programa 5 muestra el código en Python para contar el número de nodos en la lista. La referencia externa se llama actual y se inicializa en la cabeza de la lista en la línea 2. Al comienzo del proceso no hemos visto ningún nodo, por lo que la cuenta se fija en \(0\). Las líneas 4-6 implementan realmente el recorrido. Mientras la referencia actual no haya visto el final de la lista (None), nos trasladaremos a través del siguiente nodo por medio de la instrucción de asignación en la línea 6. De nuevo, es muy útil la capacidad de comparar una referencia con None. Cada vez que actual se mueve a un nuevo nodo, agregamos \(1\) a contador. Finalmente, contador es devuelto cuando termina la iteración. La Figura 9 muestra este proceso a medida que avanza en la lista.
Programa 5
1def tamano(self):
2 actual = self.cabeza
3 contador = 0
4 while actual != None:
5 contador = contador + 1
6 actual = actual.obtenerSiguiente()
7
8 return contador
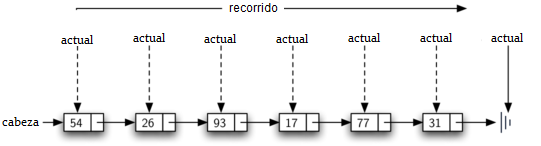
Figura 9: Recorrido de una la lista enlazada desde la cabeza hasta el final¶
Figura 9: Recorrido de una la lista enlazada desde la cabeza hasta el final
La búsqueda de un valor en una implementación de lista enlazada de una lista no ordenada también utiliza la técnica de recorrido. A medida que visitamos cada nodo en la lista enlazada nos preguntaremos si los datos almacenados allí coinciden con el elemento que estamos buscando. En este caso, sin embargo, es posible que no tengamos que recorrer todo el camino hasta el final de la lista. De hecho, si llegamos al final de la lista, eso significa que el ítem que estamos buscando no debería estar presente. También, si encontramos el ítem, no hay necesidad de continuar.
El Programa 6 muestra la implementación del método buscar. Como en el método tamano, el recorrido se inicializa para comenzar en la cabeza de la lista (línea 2). También usamos una variable booleana que se llama encontrado para recordar si hemos localizado el ítem que estamos buscando. Puesto que no hemos encontrado el ítem al principio del recorrido, encontrado puede ser inicializado en False (línea 3). La iteración en la línea 4 tiene en cuenta ambas condiciones discutidas anteriormente. Mientras haya más nodos por visitar y no hayamos encontrado el ítem que estamos buscando, seguiremos comprobando el siguiente nodo. La pregunta de la línea 5 averigua si el ítem de datos está presente en el nodo actual. En caso afirmativo, encontrado puede ser puesto en True.
Programa 6
1def buscar(self,item):
2 actual = self.cabeza
3 encontrado = False
4 while actual != None and not encontrado:
5 if actual.obtenerDato() == item:
6 encontrado = True
7 else:
8 actual = actual.obtenerSiguiente()
9
10 return encontrado
Por ejemplo, considere la invocación al método buscar averiguando por el ítem 17.
>>> milista.buscar(17)
True
Dado que 17 está en la lista, el proceso de recorrido necesita moverse solamente al nodo que contiene el 17. En ese punto, la variable encontrado es cambiada a True y la condición del while fallará, llevando al valor devuelto indicado arriba. Este proceso se puede ver en la Figura 10.
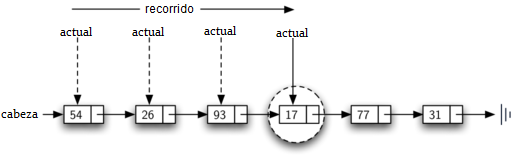
Figura 10: Búsqueda exitosa del valor 17¶
Figura 10: Búsqueda exitosa del valor 17
El método remover requiere dos pasos lógicos. En primer lugar, necesitamos recorrer la lista buscando el ítem que queremos eliminar. Una vez que encontramos el ítem (recuerde que asumimos que está presente), debemos eliminarlo. El primer paso es muy similar a buscar. Comenzando con una referencia externa puesta en la cabeza de la lista, recorremos los enlaces hasta que descubrimos el ítem que buscamos. Dado que suponemos que el ítem está presente, sabemos que la iteración se detendrá antes de que actual obtenga el valor None. Esto significa que en la condición podemos usar simplemente la variable booleana encontrado.
Cuando encontrado toma el valor True, actual será una referencia al nodo que contiene el ítem a ser removido. Pero, ¿cómo lo eliminamos? Una posibilidad sería reemplazar el valor del ítem con algún marcador que sugiera que el ítem ya no está presente. El problema con este enfoque es que el número de nodos ya no coincidirá con el número de ítems. Sería mucho mejor remover el ítem mediante la eliminación completa del nodo.
Para remover el nodo que contiene el ítem, necesitamos modificar el enlace en el nodo anterior para que se refiera al nodo que sigue después de actual. Desafortunadamente, no hay manera de retroceder en la lista enlazada. Dado que actual se refiere al nodo delante de aquél donde queremos hacer el cambio, es demasiado tarde para hacer la modificación necesaria.
La solución a este dilema es usar dos referencias externas a medida que recorremos la lista enlazada. actual se comportará igual que antes, marcando la ubicación actual del recorrido. La nueva referencia, que llamaremos previo, siempre estará un nodo detrás de actual. De esta forma, cuando actual se detenga en el nodo que se va a eliminar, previo se referirá al lugar adecuado en la lista enlazada para la modificación.
El Programa 7 muestra el método remover completo. Las líneas 2-3 asignan valores iniciales a las dos referencias. Observe que actual comienza en la cabeza de la lista como en los otros ejemplos de recorrido. previo, sin embargo, se supone que va siempre un nodo detrás de actual. Por esta razón, previo comienza con un valor de None ya que no hay ningún nodo antes de la cabeza (ver la Figura 11). La variable booleana encontrado se volverá a utilizar para controlar la iteración.
En las líneas 6-7 preguntamos si el ítem almacenado en el nodo actual es el ítem que queremos remover. En caso afirmativo, encontrado puede ser puesto en True. Si no encontramos el ítem, previo y actual deben moverse un nodo hacia adelante. Una vez más, el orden de estas dos instrucciones es crucial. previo debe moverse primero un nodo hacia adelante a la ubicación de actual. En ese momento, actual se puede mover. Este proceso se conoce a menudo como “avance de oruga” ya que previo debe alcanzar a actual antes que actual se pueda mover hacia adelante. La Figura 12 muestra el movimiento de previo y actual a medida que avanzan en la lista buscando el nodo que contiene el valor 17.
Programa 7
1def remover(self,item):
2 actual = self.cabeza
3 previo = None
4 encontrado = False
5 while not encontrado:
6 if actual.obtenerDato() == item:
7 encontrado = True
8 else:
9 previo = actual
10 actual = actual.obtenerSiguiente()
11
12 if previo == None:
13 self.cabeza = actual.obtenerSiguiente()
14 else:
15 previo.asignarSiguiente(actual.obtenerSiguiente())
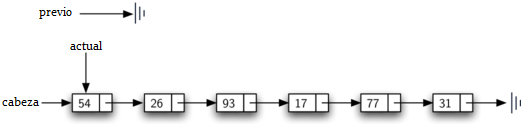
Figura 11: Valores iniciales para las referencias previo y actual¶
Figura 11: Valores iniciales para las referencias previo y actual
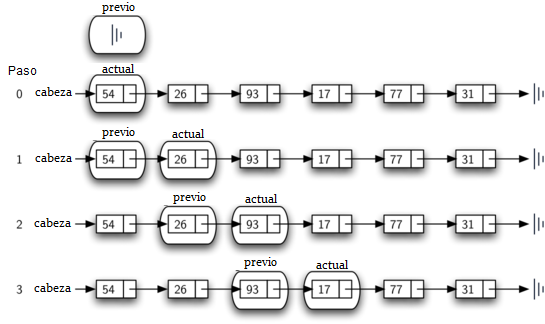
Figura 12: previo y actual se mueven por la lista¶
Figura 12: previo y actual se mueven por la lista
Una vez que se ha completado el paso de búsqueda de remover, necesitamos eliminar el nodo de la lista enlazada. La Figura 13 muestra el enlace que debe modificarse. Sin embargo, hay un caso especial que necesita ser abordado. Si resulta que el ítem a ser eliminado es el primer ítem de la lista, entonces actual hará referencia al primer nodo de la lista enlazada. Esto también significa que previo será None. Hemos dicho anteriormente que previo se referiría al nodo cuya próxima referencia necesita ser modificada para completar la eliminación. En este caso, no es previo, sino la cabeza de la lista la que necesita ser cambiada (ver la Figura 14).
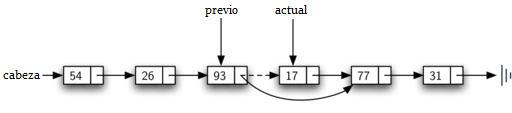
Figura 13: Eliminación de un ítem intermedio de la lista¶
Figura 13: Eliminación de un ítem intermedio de la lista
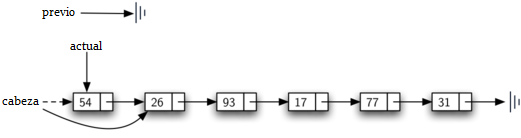
Figura 14: Remoción del primer nodo de la lista¶
Figura 14: Remoción del primer nodo de la lista
La línea 12 nos permite comprobar si estamos tratando con el caso especial descrito anteriormente. Si previo no se movió, seguirá teniendo el valor None cuando la variable booleana encontrado se vuelva True. En ese caso (línea 13), la cabeza de la lista se modifica para referirse al nodo después del nodo actual, eliminando en efecto el primer nodo de la lista enlazada. Sin embargo, si previo no es None, el nodo que se va a quitar está en algún lugar de la estructura de la lista enlazada. En este caso la referencia previo nos proporciona el nodo cuya próxima referencia debe ser cambiada. La línea 15 utiliza el método asignarSiguiente de previo para realizar la eliminación. Note que en ambos casos el destino del cambio de referencia es actual.obtenerSiguiente(). Una pregunta que surge a menudo es si los dos casos mostrados aquí también considerarán la situación en la que el elemento que se va a eliminar está en el último nodo de la lista enlazada. Dejamos ese caso para que usted lo considere.
Pruebe la clase ListaNoOrdenada en el ActiveCode 1.
Los métodos restantes anexar, insertar, indice y extraer se dejan como ejercicios. Recuerde que cada uno de estos debe tener en cuenta si el cambio se lleva a cabo en la cabeza de la lista o en algún otro lugar. Además, insertar, indice y extraer requieren que nombremos las posiciones de la lista. Asumiremos que los nombres de las posiciones son números enteros que comienzan con 0.
Autoevaluación
Parte I: Implementar el método anexar para ListaNoOrdenada. ¿Cuál es la complejidad de tiempo del método que usted creó?
Parte II: En el problema anterior, usted probablemente creó un método anexar que era \(O(n)\). Si usted agrega una instancia a la clase ListaNoOrdenada puede crear un método anexar que sea \(O(1)\). Modifique su método anexar para que sea \(O(1)\) ¡Sea cuidadoso! Para realmente hacer esto correctamente tendrá que considerar un par de casos especiales que pueden requerir que usted realice también una modificación al método agregar.