3.9. Expresiones en notaciones infija, prefija y sufija¶
Cuando usted escribe una expresión aritmética como B * C, la forma de la expresión le proporciona información para que pueda interpretarla correctamente. En este caso sabemos que la variable B está siendo multiplicada por la variable C, ya que el operador de multiplicación * aparece entre ellos en la expresión. Este tipo de notación se conoce como infija ya que el operador está entre los dos operandos sobre los que está actuando.
Considere otro ejemplo de notación infija, A + B * C. Los operadores + y * siguen apareciendo entre los operandos, pero hay un problema. ¿Sobre qué operandos actúan? ¿Opera el + sobre A y B o el * opera sobre B y C? La expresión parece ambigua.
De hecho, usted ha estado leyendo y escribiendo estos tipos de expresiones durante mucho tiempo y no le causan ningún problema. La razón de esto es que usted sabe algo sobre los operadores + y *. Cada operador tiene un nivel de precedencia. Los operadores de mayor precedencia se utilizan antes que los operadores de menor precedencia. Lo único que puede cambiar ese orden es la presencia de paréntesis. El orden de precedencia para los operadores aritméticos ubica la multiplicación y la división por encima de la suma y la resta. Si aparecen dos operadores de igual precedencia, se utiliza un ordenamiento o asociatividad de izquierda a derecha.
Interpretemos la expresión problemática A + B * C usando la precedencia de los operadores. B y C se multiplican primero y A se añade a ese resultado. (A + B) * C forzaría la suma de A y B antes de la multiplicación. En la expresión A + B + C, por precedencia (vía asociatividad), el + que está más a la izquierda operaría primero.
Aunque todo esto puede ser obvio para usted, recuerde que las computadoras necesitan saber exactamente qué operadores deben ejecutarse y en qué orden. Una forma de escribir una expresión que garantice que no habrá confusión con respecto al orden de las operaciones es crear lo que se denomina expresión completamente agrupada. Este tipo de expresión utiliza una pareja de paréntesis para cada operador. Los paréntesis dictan el orden de las operaciones; no hay ambigüedad. Tampoco es necesario recordar las reglas de precedencia.
La expresión A + B * C + D se puede reescribir como ((A + (B * C)) + D) para mostrar que la multiplicación ocurre primero, seguida por la adición que está más a la izquierda. A + B + C + D se puede escribir como ((A + B) + C) + D) ya que las operaciones de adición se asocian de izquierda a derecha.
Hay otros dos formatos de expresión muy importantes que, al principio, pueden no parecer obvios. Considere la expresión infija A + B. ¿Qué pasaría si moviéramos el operador antes de los dos operandos? La expresión resultante sería + A B. Del mismo modo, podríamos mover el operador al final. Obtendríamos A B +. Estas expresiones se ven un poco extrañas.
Estos cambios en la posición del operador con respecto a los operandos crean dos nuevos formatos de expresión, la notación prefija y la notación sufija (o postfija). La notación prefija requiere que todos los operadores precedan a los dos operandos sobre los que actúan. La notación sufija, por otro lado, requiere que sus operadores aparezcan después de los operandos correspondientes. Algunos ejemplos más deberían ayudar a hacer esto un poco más claro (ver la Tabla 2).
A + B * C se escribiría como + A * B C en la notación prefija. El operador de multiplicación aparece inmediatamente antes de los operandos B y C, denotando que el * tiene precedencia sobre el +. El operador de adición aparece entonces antes de la A y del resultado de la multiplicación.
En notación sufija, la expresión sería A B C * +. Una vez más, el orden de las operaciones se conserva ya que el * aparece inmediatamente después de la B y la C, denotando que el * tiene precedencia, con el + apareciendo después. Aunque los operadores se movieron y ahora aparecen antes o después de sus respectivos operandos, el orden de cada operando se mantuvo exactamente igual en relación con los demás.
Expresión infija |
Expresión prefija |
Expresión sufija |
|---|---|---|
A + B |
+ A B |
A B + |
A + B * C |
+ A * B C |
A B C * + |
Ahora considere la expresión infija (A + B) * C. Recuerde que en este caso, la notación infija requiere los paréntesis para forzar que se lleve a cabo la adición antes de la multiplicación. Sin embargo, cuando A + B fue escrito en notación prefija, el operador de adición fue movido simplemente antes de los operandos, + A B. El resultado de esta operación se convierte en el primer operando para la multiplicación. El operador de multiplicación se mueve delante de toda la expresión, dándonos * + A B C. Igualmente, en notación sufija A B + obliga a que la adición ocurra primero. La multiplicación se puede hacer sobre ese resultado y el operando restante C. La expresión sufija correcta es entonces A B + C *.
Considere nuevamente estas tres expresiones (ver la Tabla 3). Ha ocurrido algo muy importante. ¿A dónde se fueron los paréntesis? ¿Por qué no los necesitamos en las notaciones prefija y sufija? La respuesta es que los operadores ya no son ambiguos con respecto a los operandos sobre los que actúan. Solamente la notación infija requiere los símbolos adicionales. El orden de las operaciones dentro de las expresiones prefijas y sufijas está completamente determinado por la posición del operador y nada más. De muchas maneras, esto hace que la notación infija sea la notación menos deseable de usar.
Expresión infija |
Expresión prefija |
Expresión sufija |
|---|---|---|
(A + B) * C |
* + A B C |
A B + C * |
La Tabla 4 muestra algunos ejemplos adicionales de expresiones infijas y las expresiones equivalentes en notaciones prefija y sufija. Asegúrese de entender cómo son equivalentes en términos del orden de las operaciones que se están realizando.
Expresión infija |
Expresión prefija |
Expresión sufija |
|---|---|---|
A + B * C + D |
+ + A * B C D |
A B C * + D + |
(A + B) * (C + D) |
* + A B + C D |
A B + C D + * |
A * B + C * D |
+ * A B * C D |
A B * C D * + |
A + B + C + D |
+ + + A B C D |
A B + C + D + |
3.9.1. Conversión de expresiones infijas a notaciones prefija y sufija¶
Hasta el momento, hemos utilizado métodos ad hoc para convertir entre expresiones infijas y las expresiones equivalentes en notaciones prefija y sufija. Como es de esperar, hay formas algorítmicas para realizar la conversión que permiten transformar correctamente cualquier expresión de cualquier complejidad.
La primera técnica que vamos a considerar utiliza la noción de una expresión completamente agrupada que se discutió anteriormente. Recordemos que A + B * C se puede escribir como (A + (B * C)) para mostrar explícitamente que la multiplicación tiene precedencia sobre la adición. Sin embargo, al observar más de cerca, puede verse que cada pareja de paréntesis también indica el comienzo y el final de un par de operandos con el operador correspondiente en la mitad.
Observe el paréntesis derecho en la subexpresión (B * C) anterior. Si tuviéramos que mover el símbolo de multiplicación a esa posición y quitar el paréntesis izquierdo correspondiente, nos daría B C *, de hecho habríamos convertido la subexpresión a notación sufija. Si el operador de adición también es movido a la posición de su paréntesis derecho correspondiente y se elimina el paréntesis izquierdo que le corresponde, se produciría la expresión sufija completa (ver la Figura 6).
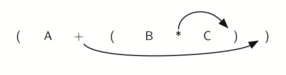
Figura 6: Traslado de operadores a la derecha para producir la notación sufija¶
Figura 6: Traslado de operadores a la derecha para producir la notación sufija
Si hacemos lo mismo pero en lugar de mover el símbolo a la posición del paréntesis derecho, lo movemos a la izquierda, obtenemos la notación prefija (ver la Figura 7). La posición de la pareja de paréntesis es en realidad una pista sobre la posición final del operador encerrado entre ellos.
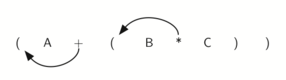
Figura 7: Traslado de operadores a la izquierda para producir la notación prefija¶
Figura 7: Traslado de operadores a la izquierda para producir la notación prefija
Así que, para convertir una expresión, independientemente de su complejidad, ya sea a notación prefija o a notación sufija, agrúpela completamente utilizando el orden de las operaciones. A continuación, mueva cada operador a la posición correspondiente de los paréntesis izquierdo o derecho dependiendo de si desea obtener la expresión en notación prefija o en notación sufija.
La siguiente es una expresión más compleja: (A + B) * C - (D - E) * (F + G). La Figura 8 muestra la conversión a las notaciones sufija y prefija.
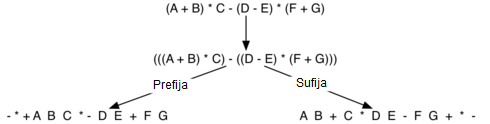
Figura 8: Conversión de una expresión compleja a notaciones prefija y sufija¶
Figura 8: Conversión de una expresión compleja a notaciones prefija y sufija
3.9.2. Conversión general de notación infija a notación sufija¶
Necesitamos desarrollar un algoritmo para convertir cualquier expresión infija a una expresión sufija. Para hacer esto vamos a examinar más de cerca el proceso de conversión.
Consideremos una vez más la expresión A + B * C. Como se muestra arriba, A B C * + es la equivalencia en notación sufija. Ya hemos observado que los operandos A, B y C permanecen en sus posiciones relativas. Sólo los operadores cambian de posición. Veamos de nuevo los operadores en la expresión infija. El primer operador que aparece de izquierda a derecha es el +. Sin embargo, en la expresión sufija, el + está al final dado que el siguiente operador, *, tiene precedencia sobre la adición. El orden de los operadores en la expresión original se invierte en la expresión sufija resultante.
A medida que procesamos la expresión, los operadores tienen que ser guardados en alguna parte, ya que sus operandos derechos correspondientes no aparecen todavía. También, el orden de estos operadores guardados puede necesitar ser invertido debido a su precedencia. Ése es el caso con la adición y la multiplicación en este ejemplo. Dado que el operador de adición aparece antes del operador de multiplicación y tiene menor precedencia, necesita aparecer después de que se use el operador de multiplicación. Debido a esta inversión del orden, tiene sentido considerar el uso de una pila para almacenar a los operadores hasta que se necesiten.
Y ¿qué ocurrirá con (A + B) * C? Recuerde que A B + C * es la equivalencia en notación sufija. De nuevo, procesando esta expresión infija de izquierda a derecha, vemos primero el +. En este caso, cuando vemos el *, el + ya se ha transcrito en la expresión de resultado porque tiene precedencia sobre el * en virtud de los paréntesis. Ahora podemos empezar a ver cómo funcionará el algoritmo de conversión. Cuando veamos un paréntesis izquierdo, lo guardaremos para indicar que habrá otro operador de alta precedencia. Ese operador tendrá que esperar hasta que aparezca el paréntesis derecho correspondiente para indicar su posición (recuerde la técnica de agrupar completamente). Cuando aparezca ese paréntesis derecho, el operador puede ser extraído de la pila.
Al recorrer la expresión infija de izquierda a derecha, usaremos una pila para almacenar los operadores. Esto proporcionará la inversión que hemos observado en el primer ejemplo. El tope de la pila siempre será el operador guardado más recientemente. Siempre que leamos a un operador nuevo, tendremos que comparar la precedencia de ese operador con la de los operadores que ya estén en la pila, si los hay.
Suponga que la expresión infija es una cadena de símbolos delimitados por espacios. Los símbolos de operaciones son *, /, + y -, junto con los paréntesis izquierdo y derecho, ( y ). Los símbolos de operandos son los identificadores de un solo carácter A, B, C, y así sucesivamente. Los siguientes pasos producirán una cadena de símbolos en el orden sufijo.
Crear una pila vacía llamada
pilaOperadorespara almacenar los operadores. Crear una lista vacía para almacenar la salida.Corvertir la cadena de entrada de notación infija a una lista, usando el método
split.Recorrer la lista de símbolos de izquierda a derecha:
Si el símbolo es un operando, agregarlo al final de la lista de salida.
Si el símbolo es un paréntesis izquierdo, enviarlo a
pilaOperadores.Si el símbolo es un paréntesis derecho, extraer de
pilaOperadoreshasta que el correspondiente paréntesis izquierdo se haya extraído. Agregar cada operador al final de la lista de salida.Si el símbolo es un operador *, /, +, ó -, incluirlo en
pilaOperadores. No obstante, extraer previamente de la pila los operadores que tengan mayor o igual precedencia y agregarlos a la lista de salida.
Cuando la expresión de entrada ha sido procesada completamente, verificar
pilaOperadores. Todos los operadores que aún estén almacenados en ella se deben enviar a la lista de salida.
La Figura 9 muestra el algoritmo de conversión trabajando sobre la expresión A * B + C * D. Observe que el primer operador * se elimina al verse el operador +. Además, el + permanece en la pila cuando aparece el segundo *, ya que la multiplicación tiene precedencia sobre la adición. Al final de la expresión infija, se extrae dos veces de la pila, eliminando ambos operadores y colocando el + como el último operador en la expresión sufija.
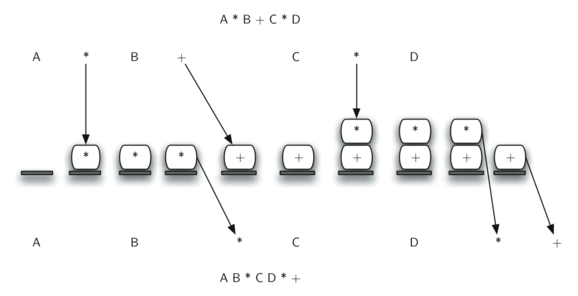
Figura 9: Conversión de A * B + C * D a notación sufija¶
Figura 9: Conversión de A * B + C * D a notación sufija
Para codificar el algoritmo en Python, usaremos un diccionario llamado precedencia para almacenar los valores de precedencia para los operadores. Este diccionario mapeará cada operador a un entero que se pueda comparar con los niveles de precedencia de otros operadores (hemos utilizado arbitrariamente los números enteros 3, 2 y 1). El paréntesis izquierdo recibirá el valor más bajo posible. De esta manera cualquier operador que se compara con él tendrá mayor precedencia y se colocará encima de él. La línea 15 define los operandos como cualquier carácter en mayúsculas o dígito. La función de conversión completa se muestra en el ActiveCode 1.
A continuación se muestran algunos ejemplos de ejecución en la consola de Python.
>>> infija_a_sufija("( A + B ) * ( C + D )")
'A B + C D + *'
>>> infija_a_sufija("( A + B ) * C")
'A B + C *'
>>> infija_a_sufija("A + B * C")
'A B C * +'
>>>
3.9.3. Evaluación de expresiones en notación sufija¶
Como ejemplo final sobre las pilas, consideraremos la evaluación de una expresión que ya está en notación sufija. En este caso, una pila será de nuevo la estructura de datos elegida. Sin embargo, al recorrer la expresión sufija, son los operandos los que deben esperar, no los operadores como en el algoritmo de conversión anterior. Otra forma de pensar en la solución es que siempre que se vea un operador en la entrada, se usarán en la evaluación los dos operandos más recientes.
Para ver esto con más detalle, considere la expresión sufija 4 5 6 * +. Al recorrer la expresión de izquierda a derecha, usted encuentra primero los operandos 4 y 5. En este punto, usted todavía no está seguro respecto a qué hacer con ellos hasta que vea el siguiente símbolo. Ubicando cada uno en la pila asegura que estén disponibles si un operador viene a continuación.
En este caso, el símbolo siguiente es otro operando. Así pues, como antes, inclúyalo en la pila y examine el símbolo siguiente. Ahora vemos un operador, *. Esto significa que los dos operandos más recientes necesitan ser utilizados en una operación de multiplicación. Al extraer dos veces de la pila, podemos obtener los operandos adecuados y luego realizar la multiplicación (en este caso obtenemos 30 como resultado).
Ahora podemos manejar este resultado colocándolo de nuevo en la pila para que pueda ser utilizado como un operando para los operadores posteriores en la expresión. Cuando se procesa el operador final, sólo quedará un valor en la pila. Se extrae y se devuelve como el resultado de la expresión. La Figura 10 muestra el contenido de la pila a medida que se procesa toda la expresión de ejemplo.
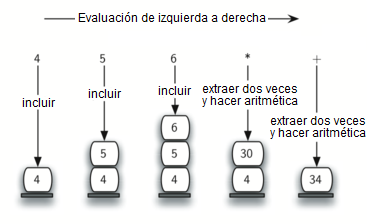
Figura 10: Contenido de la pila durante la evaluación¶
Figura 10: Contenido de la pila durante la evaluación
La Figura 11 muestra un ejemplo un poco más complejo, 7 8 + 3 2 + /. Hay dos cosas a tener en cuenta en este ejemplo. En primer lugar, el tamaño de la pila crece, disminuye y, a continuación, crece de nuevo a medida que las subexpresiones se evalúan. En segundo lugar, la operación de división necesita ser manejada cuidadosamente. Recuerde que los operandos en la expresión sufija están en su orden original ya que la notación sufija cambia sólo la ubicación de los operadores. Cuando los operandos para la división se extraen de la pila, estos se invierten. Dado que la división no es un operador conmutativo, en otras palabras \(15/5\) no es lo mismo que \(5/15\), debemos estar seguros de que el orden de los operandos no esté intercambiado.
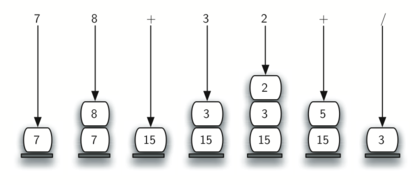
Figura 11: Un ejemplo más complejo de evaluación¶
Figura 11: Un ejemplo más complejo de evaluación
Supongamos que la expresión sufija es una cadena de símbolos delimitados por espacios. Los operadores son *, /, + y -; además, se supone que los operandos son valores enteros de un solo dígito. La salida será un resultado entero.
Crear una pila vacía llamada
pilaOperandos.Convertir la cadena a una lista mediante la aplicación del método
split.Recorrer la lista de símbolos de izquierda a derecha.
Si el símbolo es un operando, convertirlo de tipo cadena a tipo entero e incluir el valor en
pilaOperandos.Si el símbolo es un operador, *, /, +, ó -, éste necesitará dos operandos. Extraer dos veces de
pilaOperandos. La primera extracción corresponde al segundo operando y la segunda al primer operando. Realizar la operación aritmética. Incluir el resultado enpilaOperandos.
Cuando la expresión de entrada se ha procesado completamente, el resultado queda en la pila. Extraerlo de
pilaOperandosy devolver dicho valor.
La función completa para la evaluación de expresiones sufijas se muestra en el ActiveCode 2. Para ayudar con la aritmética, se define una función auxiliar hacerAritmetica que tomará dos operandos y un operador y luego realizará la operación aritmética apropiada.
Es importante tener en cuenta que tanto en el programa de conversión de expresiones sufijas como en el programa de evaluación de expresiones sufijas asumimos que no había errores en la expresión de entrada. Utilizando estos programas como punto de partida, usted puede fácilmente pensar cómo podría incluirse una detección de errores y la generación de informes. Dejamos esto como un ejercicio para el final del capítulo.
Autoevaluación