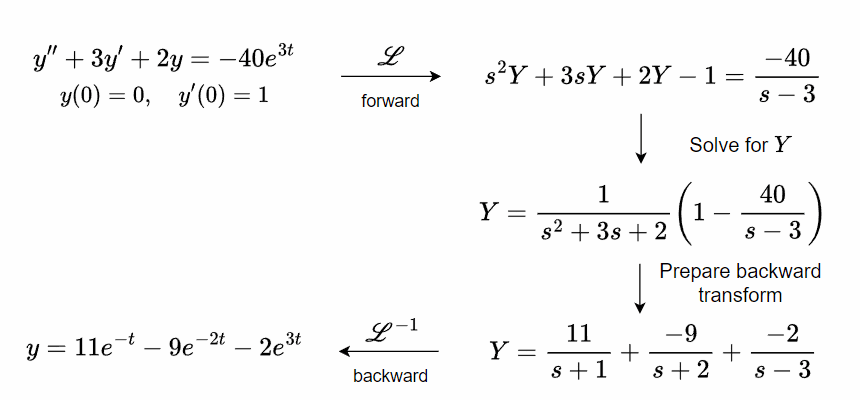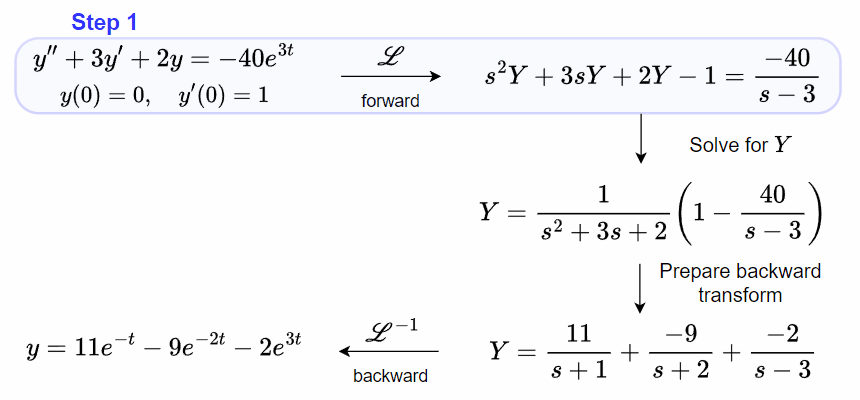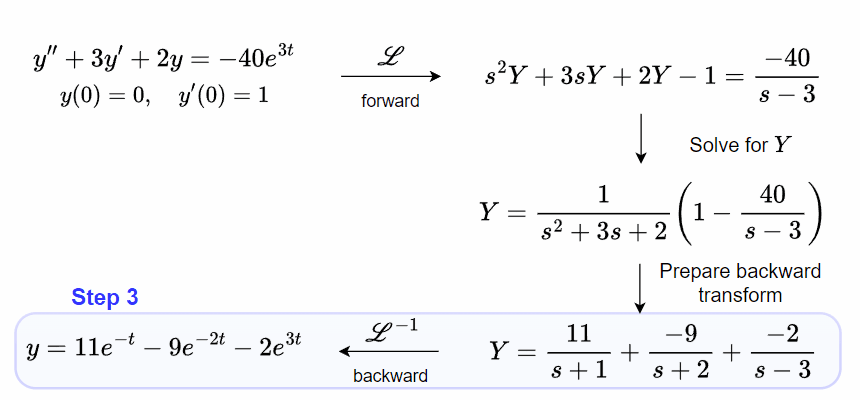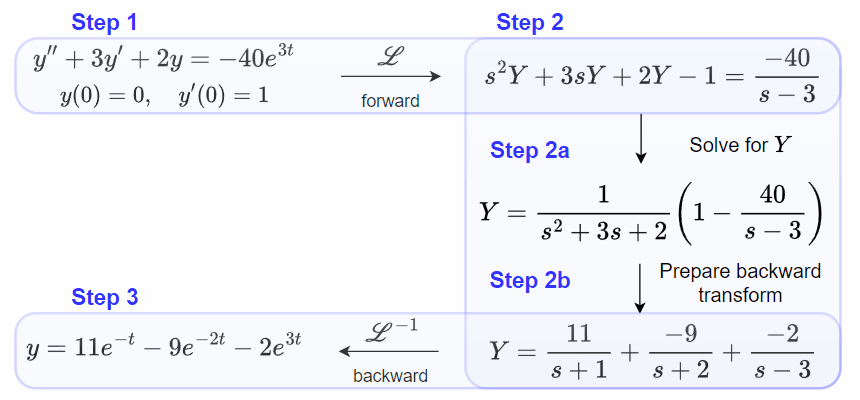
Part IV Laplace Transform Method
Solving an algebraic equation often involves isolating the unknown variable. However, in differential equations, the unknown is entangled within derivatives, making isolation more challenging. The Laplace Transform offers a powerful technique to temporarily reframe the equation, effectively “unwrapping” the derivatives and enabling a more straightforward isolation of the unknown, similar to algebra.
By applying the Laplace Transform, the dependent variable is extracted from its derivatives and embedded within a special integral. This integral serves as a “container” that encapsulates the unknown function we seek. In this transformed state, these containers can be manipulated algebraically, allowing us to isolate the unknown function within. Once isolated, we can then revert the transform, releasing the function and revealing the solution.
In essence, the Laplace Transform alters the mathematical landscape of a differential equation, simplifying the process of solving for the unknown function. This method is particularly powerful for tackling linear non-constant coefficient (LNCC) equations with discontinuous right-hand side functions.
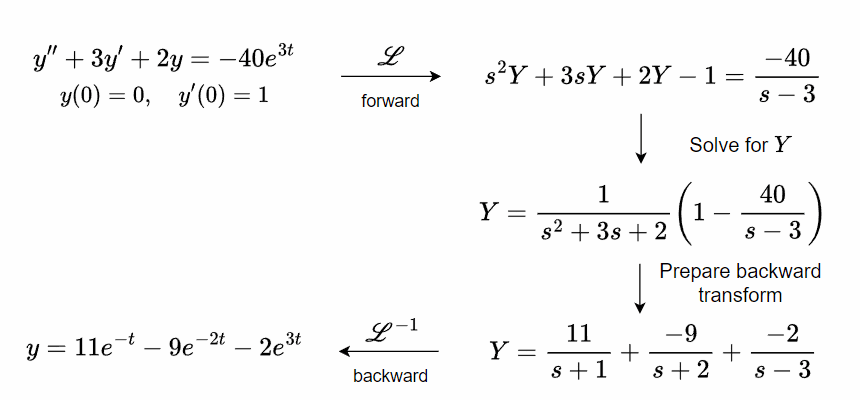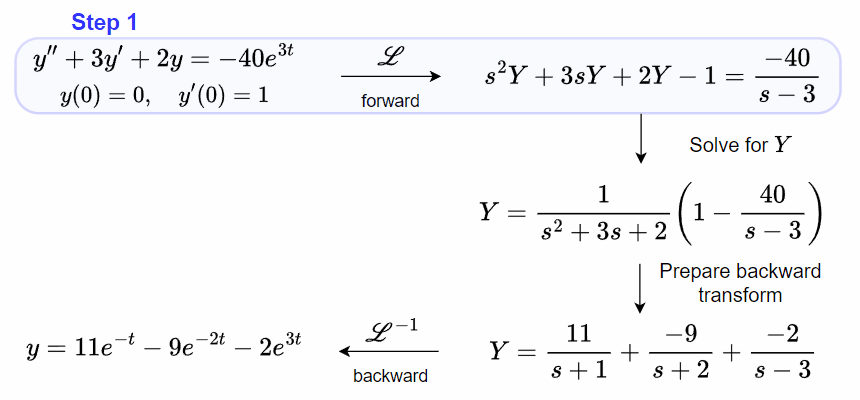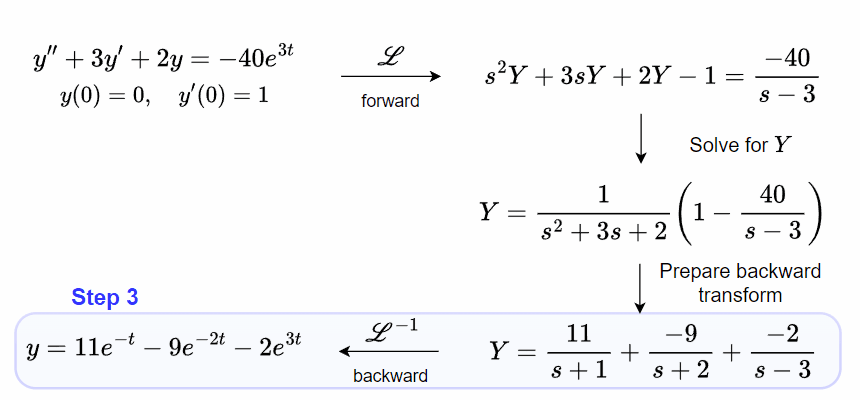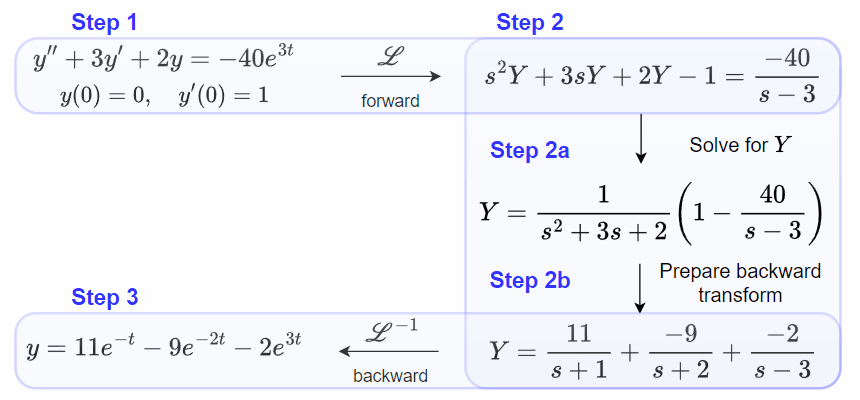
Throughout this chapter, we will frequently refer to this roadmap and apply it to the initial-value problem,
\begin{gather}
y'' + 3y' + 2y = -40e^{3t},\tag{44}\\
y(0) = 0, \quad y'(0) = 1,\tag{45}
\end{gather}
as a guiding example to illustrate the key concepts.

