8.13. Sorting Efficiency¶

To figure out how efficient the Selection Sort algorithm is, we will analyze the worst case. For units of work, we will consider comparisons and swaps - the two key operations in a sort. This video works through how much work there is for a Selection Sort on a list of 4 items:

Animation used by permission of Virginia Tech

If we did the same work for a selection sort on a list of 100 things ( $n = 100$ ), it would look like:

Step	Comparisons	Swaps
1	99	1
2	98	1
3	97	1
…	…	…
97	3	1
98	2	1
99	1	1

The total swaps would be 99 steps times 1 swap each = 99. Expressed in terms of $n$ we could say it is $n - 1$ swaps.

The total comparisons would be 99 + 98 + 97 + … + 3 + 2 + 1 or $(n - 1) + (n - 2) + (n - 3) + . . . + 3 + 2 + 1$ . So what does that equal? There is a trick to find out - pair up the first item and the last, then the second item and next to last and so on. Each pair of items sums to $n$ :

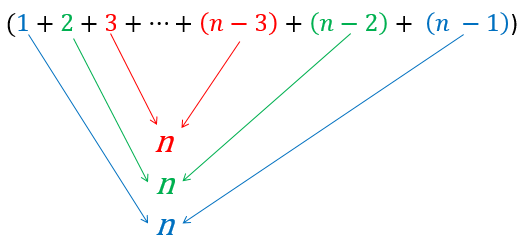
Since there were $n - 1$ numbers to start with, there will be $\frac{n - 1}{2}$ pairs, each of which adds to $n$ . Multiplying the number of pairs by the sum of each pair gives us the total: $\frac{n - 1}{2} \cdot n = \frac{n^{2} - n}{2} = \frac{n^{2}}{2} - \frac{n}{2}$ .

Overall, our work will be given by:

$Total work = Comparisons + Swaps$

Or:

$Total work = (\frac{n^{2}}{2} - \frac{n}{2}) + (n - 1) = \frac{n^{2}}{2} + \frac{n}{2} - 1$

Since for Big-O purposes, all we care about is the class of the dominant term, in this case $\frac{n^{2}}{2}$ , we will say that Selection Sort is $O (n^{2})$ (Quadratic). A similar process can be used to show that so is Insertion Sort.

Important

Selection and Insertion Sort are Quadratic - $O (n^{2})$ .

You have attempted 1 of 2 activities on this page