6.11. Implementación de un montículo binario¶
6.11.1. La propiedad de estructura¶
Para lograr que nuestro montículo funcione eficientemente, aprovecharemos la naturaleza logarítmica del árbol binario para representar nuestro montículo. Para garantizar un rendimiento logarítmico, debemos mantener a nuestro árbol equilibrado. Un árbol binario equilibrado tiene aproximadamente el mismo número de nodos en los subárboles izquierdo y derecho de la raíz. En nuestra implementación del montículo mantenemos al árbol equilibrado creando un árbol binario completo. Un árbol binario completo es un árbol en el que cada nivel tiene todos sus nodos. La excepción a esta regla es el nivel inferior del árbol, el cual llenamos de izquierda a derecha. La Figura 1 muestra un ejemplo de un árbol binario completo.
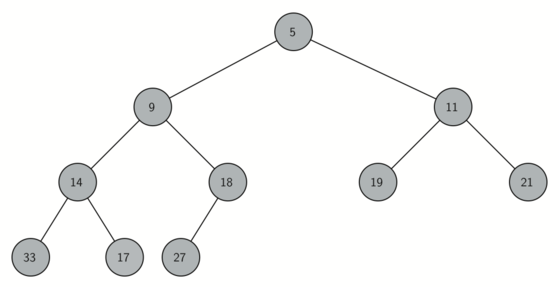
Figura 1: Un árbol binario completo¶
Figura 1: Un árbol binario completo
Otra propiedad interesante de un árbol completo es que podemos representarlo usando una sola lista. No necesitamos usar nodos y referencias ni incluso listas de listas. Debido a que el árbol está completo, el hijo izquierdo de un padre (en la posición \(p\)) es el nodo que se encuentra en la posición \(2p\) en la lista. Del mismo modo, el hijo derecho del padre está en la posición \(2p + 1\) en la lista. Para encontrar el padre de cualquier nodo en el árbol, podemos simplemente usar la división entera de Python. Dado que un nodo esté en la posición \(n\) en la lista, el padre está en la posición \(n/2\). La Figura 2 muestra un árbol binario completo junto con la representación de lista para el árbol. Note la relación \(2p\) y \(2p+1\) entre el padre y los hijos. La representación de lista para el árbol, junto con la propiedad de estructura completa, nos permite recorrer eficientemente un árbol binario completo usando sólo unas cuantas operaciones matemáticas simples. Veremos que esto también conduce a una implementación eficiente de nuestro montículo binario.
6.11.2. La propiedad de orden del montículo¶
El método que usaremos para almacenar ítems en un montículo depende de mantener la propiedad de orden del montículo. La propiedad de orden del montículo es la siguiente: En un montículo, para cada nodo \(x\) con padre \(p\), la clave en \(p\) es menor o igual a la clave en \(x\). La Figura 2 también ilustra un árbol binario completo que posee la propiedad de orden del montículo.
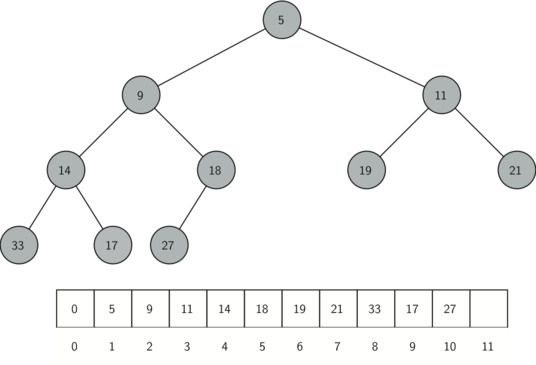
Figura 2: Un árbol binario completo, junto con su representación de lista¶
Figura 2: Un árbol binario completo, junto con su representación de lista
6.11.3. Operaciones con montículos¶
Comenzaremos nuestra implementación de un montículo binario con el constructor. Puesto que todo el montículo binario puede ser representado por una sola lista, todo lo que el constructor hará es inicializar la lista y un atributo tamanoActual para realizar un seguimiento del tamaño actual del montículo. El Programa 1 muestra el código en Python para el constructor. Usted notará que un montículo binario vacío tiene un cero solo como primer elemento de listaMonticulo y que este cero no se usa, pero está ahí para que la división entera simple pueda usarse en métodos posteriores.
Programa 1
class MonticuloBinario:
def __init__(self):
self.listaMonticulo = [0]
self.tamanoActual = 0
El siguiente método que implementaremos es insertar. La manera más fácil y eficiente de agregar un ítem a una lista es simplemente añadir el elemento al final de la lista. La buena noticia respecto a la inserción al final de la lista es que garantiza que mantendremos la propiedad de estructura completa del árbol. La malas noticia sobre ella es que muy probablemente violaremos la propiedad de estructura del montículo. Sin embargo, es posible escribir un método que nos permitirá recuperar la propiedad de estructura del montículo comparando el ítem recién agregado con su padre. Si el ítem recién agregado es menor que su padre, entonces podemos intercambiar el ítem con su padre. La Figura 2 muestra la serie de intercambios necesarios para infiltrar hacia arriba el ítem recién agregado hasta su posición correcta en el árbol.
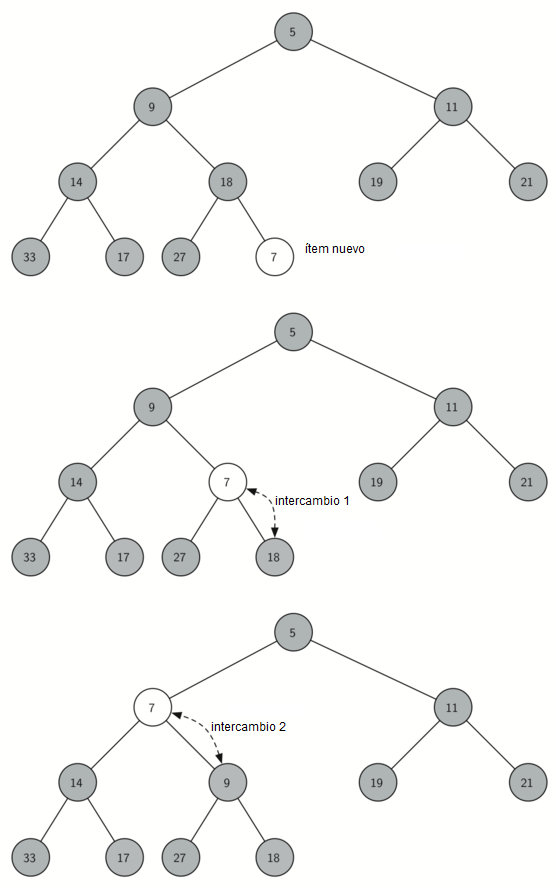
Figura 2: Infiltración del nuevo nodo hasta su posición correcta¶
Figura 2: Infiltración del nuevo nodo hasta su posición correcta
Tenga en cuenta que cuando infiltramos un ítem hacia arriba, estamos restaurando la propiedad de montículo entre el ítem recién agregado y el padre. También estamos preservando la propiedad de montículo para cualesquiera hermanos. Por supuesto, si el ítem recién agregado es muy pequeño, es posible que tengamos que cambiarlo a otro nivel superior. De hecho, es posible que tengamos que seguir haciendo intercambios hasta llegar a la parte superior del árbol. El Programa 2 muestra el método infiltArriba, el cual infiltra un nuevo ítem hacia arriba en el árbol hasta donde sea necesario para mantener la propiedad de montículo. Es aquí donde nuestro elemento desperdiciado en listaMonticulo resulta importante. Observe que podemos calcular el padre de cualquier nodo utilizando la división entera simple. El padre del nodo actual se puede calcular dividiendo el índice del nodo actual por 2.
Ahora estamos listos para escribir el método insertar (ver el Programa 3). La mayor parte del trabajo en el método insertar es hecho realmente por infiltArriba. Una vez que se añade un nuevo ítem al árbol (al final de su lista), infiltArriba se hace cargo y posiciona el nuevo ítem apropiadamente.
Programa 2
def infiltArriba(self,i):
while i // 2 > 0:
if self.listaMonticulo[i] < self.listaMonticulo[i // 2]:
tmp = self.listaMonticulo[i // 2]
self.listaMonticulo[i // 2] = self.listaMonticulo[i]
self.listaMonticulo[i] = tmp
i = i // 2
Programa 3
def insertar(self,k):
self.listaMonticulo.append(k)
self.tamanoActual = self.tamanoActual + 1
self.infiltArriba(self.tamanoActual)
Con el método insertar correctamente definido, ahora podemos examinar el método eliminarMin. La propiedad de montículo requiere que la raíz del árbol sea el ítem más pequeño del árbol, encontrar el ítem mínimo es fácil. La parte difícil de eliminarMin es restaurar el cumplimiento total de la estructura de montículo y las propiedades de orden del montículo después de que se haya eliminado la raíz. Podemos restaurar nuestro montículo en dos pasos. Primero, restauraremos el ítem raíz tomando el último ítem de la lista y moviéndolo a la posición de la raíz. Mover el último ítem preserva nuestra propiedad de estructura de montículo. Sin embargo, probablemente hemos destruido la propiedad de orden de montículo de nuestro montículo binario. En segundo lugar, restauraremos la propiedad de orden de montículo empujando el nuevo nodo raíz hacia abajo del árbol hasta su posición correcta. La Figura 3 muestra la serie de intercambios necesarios para mover el nuevo nodo raíz a su posición correcta en el montículo.
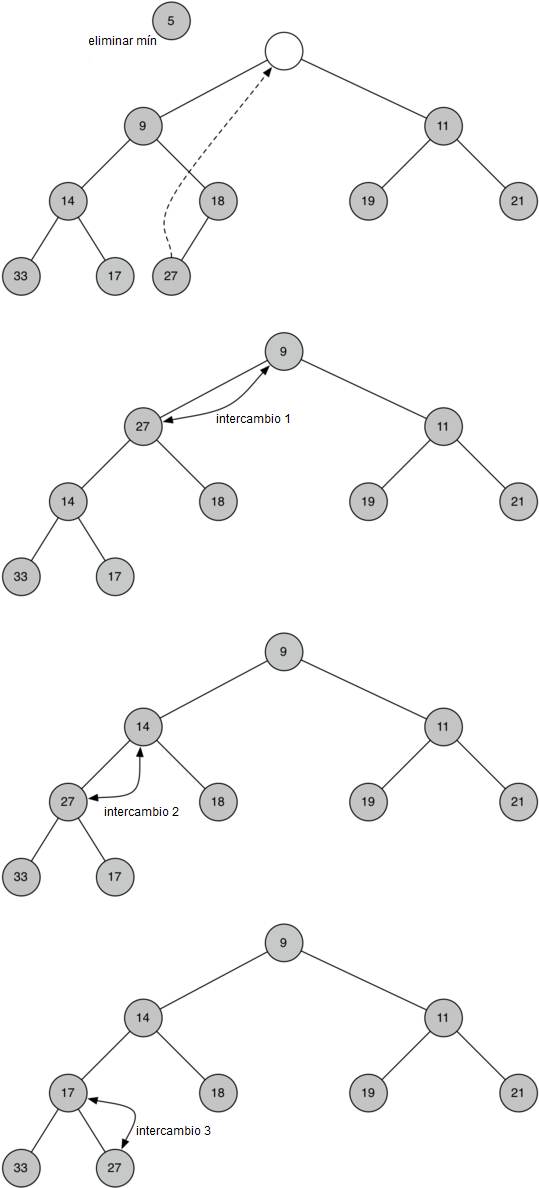
Figura 3: Infiltración del nodo raíz hacia abajo en el árbol¶
Figura 3: Infiltración del nodo raíz hacia abajo en el árbol
Para mantener la propiedad de orden del montículo, todo lo que necesitamos hacer es intercambiar la raíz con su hijo que sea menor que la raíz. Después del intercambio inicial, podemos repetir el proceso de intercambio con un nodo y sus hijos hasta que el nodo sea intercambiado a una posición en el árbol donde ya sea menor que ambos. El código para infiltrar un nodo hacia abajo en el árbol se encuentra en los métodos infiltAbajo e hijoMin en el Programa 4.
Programa 4
def infiltAbajo(self,i):
while (i * 2) <= self.tamanoActual:
hm = self.hijoMin(i)
if self.listaMonticulo[i] > self.listaMonticulo[hm]:
tmp = self.listaMonticulo[i]
self.listaMonticulo[i] = self.listaMonticulo[hm]
self.listaMonticulo[hm] = tmp
i = hm
def hijoMin(self,i):
if i * 2 + 1 > self.tamanoActual:
return i * 2
else:
if self.listaMonticulo[i*2] < self.listaMonticulo[i*2+1]:
return i * 2
else:
return i * 2 + 1
El código para la operación eliminarMin está en el Programa 5. Tenga en cuenta que una vez más el trabajo duro es manejado por una función de ayuda, en este caso infiltAbajo.
Programa 5
def eliminarMin(self):
valorSacado = self.listaMonticulo[1]
self.listaMonticulo[1] = self.listaMonticulo[self.tamanoActual]
self.tamanoActual = self.tamanoActual - 1
self.listaMonticulo.pop()
self.infiltAbajo(1)
return valorSacado
Para terminar nuestra discusión sobre montículos binarios, vamos a mirar un método para construir un montículo completo a partir de una lista de claves. El primer método en el que usted podría pensar puede ser como el siguiente. Dada una lista de claves, usted podría crear un montículo fácilmente insertando cada clave una a la vez. Puesto que usted está comenzando con una lista de un ítem, la lista está ordenada y podría usar la búsqueda binaria para encontrar la posición correcta para insertar la clave siguiente a un costo de aproximadamente \(O(\log{n})\). Sin embargo, recuerde que la inserción de un elemento en el centro de la lista puede requerir \(O(n)\) operaciones para desplazar el resto de la lista con el fin de dar cabida a la nueva clave. Por lo tanto, insertar \(n\) claves en el montículo requeriría un total de \(O(n\log{n})\) operaciones. No obstante, si empezamos con una lista completa, entonces podemos construir todo el montículo en \(O(n)\) operaciones. El Programa 6 muestra el código para construir todo el montículo.
Programa 6
def construirMonticulo(self,unaLista):
i = len(unaLista) // 2
self.tamanoActual = len(unaLista)
self.listaMonticulo = [0] + unaLista[:]
while (i > 0):
self.infiltAbajo(i)
i = i - 1
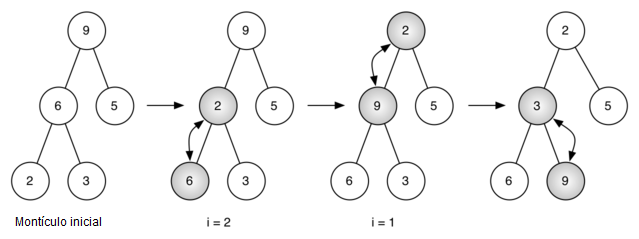
Figura 4: Construcción de un montículo a partir de la lista [9, 6, 5, 2, 3]¶
Figura 4: Construcción de un montículo a partir de la lista [9, 6, 5, 2, 3]
La Figura 4 muestra los intercambios que el método construirMonticulo hace a medida que mueve los nodos en un árbol inicial de [9, 6, 5, 2, 3] a sus posiciones correctas. Aunque comenzamos en la mitad del árbol y nos devolvemos hacia la raíz, el método infiltAbajo asegura que el hijo más grande siempre es desplazado hacia abajo en el árbol. Debido a que el montículo es un árbol binario completo, cualesquiera nodos más allá del punto medio será hojas y por lo tanto no tienen hijos. Observe que cuando i = 1, estamos infiltrando hacia abajo desde la raíz del árbol, por lo que esto puede requerir múltiples intercambios. Como se puede ver en los árboles de más a la derecha en la Figura 4, primero es retirado el 9 de la posición raíz, pero después que el 9 se mueve un nivel hacia abajo en el árbol, infiltAbajo asegura que revisemos el siguiente conjunto de hijos más abajo en el árbol para asegurarnos de que el 9 se empuje tan abajo como pueda ir. En este caso resulta un segundo intercambio con 3. Ahora que el 9 se ha movido al nivel más bajo del árbol, no se pueden hacer más intercambios. Es útil comparar la representación de lista de esta serie de intercambios como se muestra en la Figura 4 con la representación de árbol.
i = 2 [0, 9, 5, 6, 2, 3]
i = 1 [0, 9, 2, 6, 5, 3]
i = 0 [0, 2, 3, 6, 5, 9]
La implementacón completa del montículo binario se puede ver en el ActiveCode 1.
La afirmación de que podemos construir el montículo en \(O(n)\) puede parecer un poco misteriosa al principio, y una prueba está más allá del alcance de este libro. Sin embargo, la clave para entender que usted puede construir el montículo en \(O(n)\) es recordar que el factor \(\log{n}\) se deriva de la altura del árbol. Para la mayor parte del trabajo en construirMonticulo, el árbol es más bajo que \(\log{n}\).
Usando el hecho de que usted puede construir un montículo a partir de una lista en tiempo \(O(n)\), usted construirá, como ejercicio al final de este capítulo, un algoritmo de ordenamiento que use un montículo y ordene una lista en \(O(n\log{n}))\).