7.12. Construcción del grafo de la gira del caballo¶
Para representar como un grafo el problema de la gira del caballo usaremos las dos ideas siguientes: Cada cuadrado en el tablero de ajedrez puede representarse como un nodo del grafo. Cada movimiento legal del caballo puede representarse como una arista del grafo. La Figura 1 ilustra, en un grafo, los movimientos legales de un caballo y las aristas correspondientes.
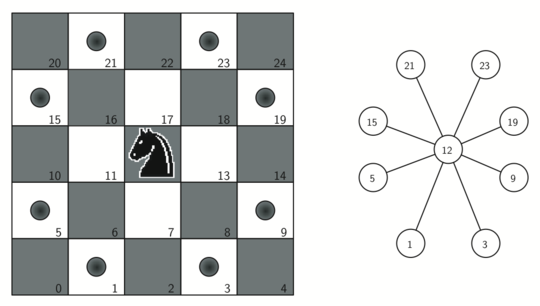
Figura 1: Movimientos legales para un caballo ubicado en el cuadrado 12, y el grafo correspondiente¶
Figura 1: Movimientos legales para un caballo ubicado en el cuadrado 12, y el grafo correspondiente
Podemos usar la función en Python mostrada en el Programa 1 para construir el grafo completo de un tablero n-por-n, . La función grafoDelCaballo da una pasada por el tablero completo. En cada cuadrado del tablero la función grafoDelCaballo llama a una función auxiliar, generarMovLegales, para crear una lista de movimientos legales para esa posición en el tablero. Todos los movimientos legales se convierten en aristas del grafo. Otra función auxiliar pos_A_Id_Nodo convierte una posición en el tablero, dada originalmente en términos de una fila y una columna, en un número de vértice lineal similar a los números de vértice mostrados en la Figura 1.
Programa 1
from pythoned.grafos import Grafo
def grafoDelCaballo(tamanoTablero):
grafoCbllo = Grafo()
for fil in range(tamanoTablero):
for col in range(tamanoTablero):
idNodo = pos_A_Id_Nodo(fil,col,tamanoTablero)
posicionesNuevas = generarMovLegales(fil,col,tamanoTablero)
for e in posicionesNuevas:
nid = pos_A_Id_Nodo(e[0],e[1],tamanoTablero)
grafoCbllo.agregarArista(idNodo,nid)
return grafoCbllo
def pos_A_Id_Nodo(fila, columna, tamano_del_tablero):
return (fila * tamano_del_tablero) + columna
La función generarMovLegales (Programa 2) toma la posición del caballo en el tablero y genera cada uno de los ocho movimientos posibles. La función auxiliar coordLegal (Programa 2) asegura que un movimiento particular que se genere todavía esté aún dentro del tablero.
Programa 2
def generarMovLegales(x,y,tamanoTablero):
nuevosMovimientos = []
desplazamientosEnL = [(-1,-2),(-1,2),(-2,-1),(-2,1),
( 1,-2),( 1,2),( 2,-1),( 2,1)]
for i in desplazamientosEnL:
nuevoX = x + i[0]
nuevoY = y + i[1]
if coordLegal(nuevoX,tamanoTablero) and \
coordLegal(nuevoY,tamanoTablero):
nuevosMovimientos.append((nuevoX,nuevoY))
return nuevosMovimientos
def coordLegal(x,tamanoTablero):
if x >= 0 and x < tamanoTablero:
return True
else:
return False
La Figura 2 muestra el grafo completo de los posibles movimientos en una tablero de ocho por ocho. Hay exactamente 336 aristas en el grafo. Note que los vértices correspondientes a las aristas del tablero tienen menos conexiones (movimientos legales) que los vértices del centro del tablero. Una vez más podemos ver cuán ralo es el grafo. Si el grafo estuviera completamente conectado, habría 4,096 aristas. Dado que sólo hay 336 aristas, la matriz de adyacencia estaría llena sólo en un 8.2 por ciento.

Figura 2: Todos los movimientos legales para un caballo en un tablero de ajedrez de \(8 \times 8\)¶
Figura 2: Todos los movimientos legales para un caballo en un tablero de ajedrez de \(8 \times 8\)