2.3. Notación O-grande¶
Al tratar de caracterizar la eficiencia de un algoritmo en términos del tiempo de ejecución, independientemente de cualquier programa o computadora en particular, es importante cuantificar el número de operaciones o pasos que el algoritmo requerirá. Si se considera que cada uno de estos pasos es una unidad básica de cálculo, entonces el tiempo de ejecución de un algoritmo puede expresarse como el número de pasos necesarios para resolver el problema. Decidir sobre una unidad básica de cálculo apropiada puede ser un problema complicado y dependerá de cómo se implemente el algoritmo.
Una buena unidad básica de cálculo para comparar los algoritmos de sumatoria mostrados anteriormente podría ser contar el número de instrucciones de asignación realizadas para calcular la suma. En la función sumaDeN, el número de instrucciones de asignación es 1 (\(laSuma = 0\)) más el valor de n (el número de veces que ejecutamos \(laSuma=laSuma+i\)). Podemos denotar esto por una función, digamos T, donde \(T(n)=1 + n\). El parámetro n a menudo se denomina el “tamaño del problema”, y podemos interpretar la función como “T(n) es el tiempo que se necesita para resolver un problema de tamaño n, a saber, 1+n pasos”.
En las funciones de sumatoria mencionadas anteriormente, tiene sentido utilizar el número de términos en la sumatoria para indicar el tamaño del problema. Podemos decir entonces que la suma de los primeros 100,000 enteros es un caso más grande del problema de la suma que la suma de los primeros 1,000. Debido a esto, podría parecer razonable que el tiempo requerido para resolver el caso más grande fuera mayor que para el caso más pequeño. Nuestro objetivo entonces es mostrar cómo cambia el tiempo de ejecución del algoritmo con respecto al tamaño del problema.
Los científicos de la computación prefieren llevar esta técnica de análisis un poco más allá. Resulta que el número exacto de operaciones no es tan importante como determinar la parte más dominante de la función \(T(n)\). En otras palabras, a medida que el problema se hace más grande, una parte de la función \(T(n)\) tiende a dominar la parte restante. Este término dominante es lo que, al final, se utiliza para la comparación. La función orden de magnitud describe la parte de \(T(n)\) que más rápido crece a medida que aumenta el valor de n. El orden de magnitud es a menudo llamado notación O-grande (por “orden”) y se escribe como \(O(f(n))\). Esta notación proporciona una aproximación útil al número real de pasos en el cálculo. La función \(f(n)\) brinda una representación sencilla de la parte dominante de la función \(T(n)\) original.
En el ejemplo anterior, \(T(n)=1+n\). A medida que n se hace grande, la constante 1 será cada vez menos significativa para el resultado final. Si estamos buscando una aproximación para \(T(n)\), entonces podemos despreciar el 1 y simplemente decir que el tiempo de ejecución es \(O(n)\). Es importante notar que el 1 es ciertamente significativo para \(T(n)\). No obstante, a medida que n se hace grande, nuestra aproximación será igualmente exacta sin él.
Como ejemplo alternativo, supongamos que para algún algoritmo, el número exacto de pasos es \(T(n)=5n^{2}+27n+1005\). Cuando n es pequeño, digamos 1 ó 2, la constante 1005 parece ser la parte dominante de la función. Sin embargo, a medida que n se hace más grande, el término \(n^{2}\) se convierte en el más importante. De hecho, cuando n es realmente grande, los otros dos términos se vuelven insignificantes en el papel que desempeñan para la determinación del resultado final. Una vez más, para aproximar \(T(n)\) a medida que n se hace grande, podemos ignorar los otros términos y concentrarnos en \(5n^{2}\). Además, el coeficiente \(5\) se vuelve insignificante cuando n se hace grande. Podemos decir entonces que la función \(T(n)\) tiene un orden de magnitud \(f(n)=n^{2}\), o simplemente que es \(O(n^{2})\).
Aunque no vemos esto en el ejemplo de la suma, a veces el rendimiento de un algoritmo depende de los valores exactos de los datos en lugar de simplemente el tamaño del problema. Para este tipo de algoritmos necesitamos caracterizar su desempeño en términos del mejor caso, el peor caso, o el caso promedio. El peor caso de rendimiento se refiere a un conjunto de datos en particular, donde el algoritmo se comporta especialmente mal. Mientras que un conjunto de datos diferente para el mismo algoritmo podría tener un rendimiento extraordinariamente bueno. Sin embargo, en la mayoría de los casos, el algoritmo se comporta de algún modo entre estos dos extremos (caso promedio). Es importante que un científico de la computación entienda estas distinciones para que no resulten engañosas en un caso particular.
Una serie de funciones de orden de magnitud muy comunes aparecerán una y otra vez a medida que usted estudia algoritmos. Éstas se muestran en la Tabla 1. Para decidir cuál de estas funciones es la parte dominante de cualquier función \(T(n)\), debemos compararlas entre sí a medida que n se hace grande.
f(n) |
Nombre |
|---|---|
\(1\) |
Constante |
\(\log n\) |
Logarítmica |
\(n\) |
Lineal |
\(n\log n\) |
Log-lineal |
\(n^{2}\) |
Cuadrática |
\(n^{3}\) |
Cúbica |
\(2^{n}\) |
Exponencial |
La Figura 1 muestra las gráficas de las funciones comunes de la Tabla 1. Note que cuando n es pequeño, las funciones no están muy bien definidas una con respecto a otra. Es difícil saber cuál es la dominante. Sin embargo, a medida que n crece, existe una relación definida y es fácil compararlas entre sí.
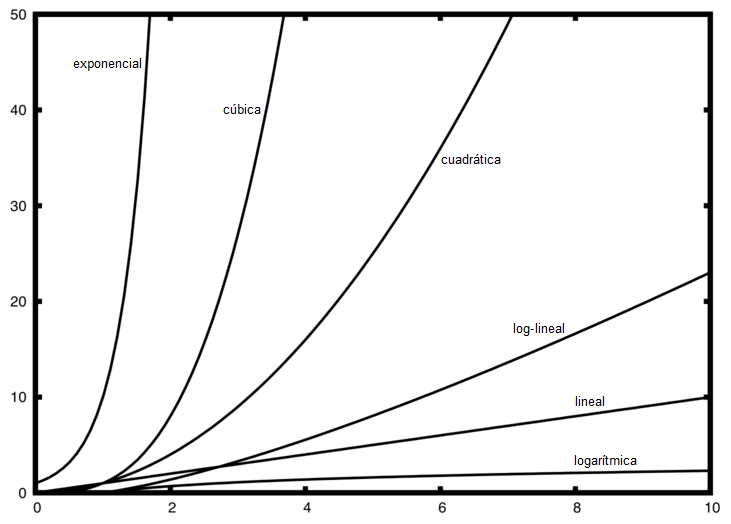
Figura 1: Gráficas de las funciones comunes para la notación O-grande¶
Figura 1: Gráficas de las funciones comunes para la notación O-grande
Como ejemplo final, supongamos que tenemos el fragmento de código en Python que se muestra en el Programa 2. Aunque este programa realmente no hace nada, es instructivo ver cómo podemos considerar el código real y analizar su rendimiento.
Programa 2
a=5
b=6
c=10
for i in range(n):
for j in range(n):
x = i * i
y = j * j
z = i * j
for k in range(n):
w = a*k + 45
v = b*b
d = 33
El número de operaciones de asignación es la suma de cuatro términos. El primer término es la constante 3, que representa las tres instrucciones de asignación al inicio del fragmento de código. El segundo término es \(3n^ {2}\), ya que hay tres declaraciones que se realizan \(n^{2}\) veces debido a la iteración anidada. El tercer término es \(2n\), dos instrucciones que se repiten n veces. Finalmente, el cuarto término es la constante 1, que representa la instrucción de asignación final. Esto nos da \(T(n)=3+3n^{2}+2n+1=3n^{2}+2n+4\). Observando los exponentes, podemos notar fácilmente que el término \(n^{2}\) será dominante y por lo tanto este fragmento de código es \(O(n^{2})\). Tenga en cuenta que todos los otros términos, así como el coeficiente en el término dominante, se pueden ignorar a medida que n crece más.
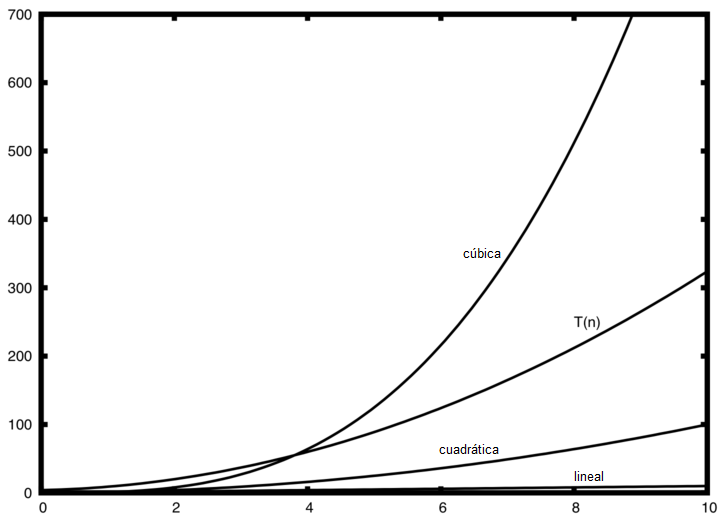
Figura 2: Comparación de \(T(n)\) con funciones comunes para la notación O-grande¶
Figura 2: Comparación de \(T(n)\) con funciones comunes para la notación O-grande
La Figura 2 muestra algunas de las funciones comunes para la notación O-grande comparadas con la función \(T (n)\) discutida anteriormente. Tenga en cuenta que \(T(n)\) es inicialmente mayor que la función cúbica. Sin embargo, a medida que n crece, la función cúbica rápidamente supera \(T(n)\). Es fácil ver que \(T(n)\) sigue entonces a la función cuadrática a medida que \(n\) continúa creciendo.
Autoevaluación
Escriba dos funciones en Python para encontrar el número mínimo en una lista. La primera función debe comparar cada número de una lista con todos los demás de la lista. \(O(n^2)\). La segunda función debe ser lineal \(O(n)\).