6.22. Exercises

  1. Draw the tree structure resulting from the following set of tree function calls:

    >>> r = BinaryTree(3)
>>> insert_left(r, 4)
[3, [4, [], []], []]
>>> insert_left(r, 5)
[3, [5, [4, [], []], []], []]
>>> insert_right(r, 6)
[3, [5, [4, [], []], []], [6, [], []]]
>>> insert_right(r, 7)
[3, [5, [4, [], []], []], [7, [], [6, [], []]]]
>>> set_root_val(r, 9)
>>> insert_left(r, 11)
[9, [11, [5, [4, [], []], []], []], [7, [], [6, [], []]]]

  2. Trace the algorithm for creating an expression tree for the expression (4∗8)/6−3.

  3. Consider the following list of integers: [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]. Show the binary search tree resulting from inserting the integers in the list.

  4. Consider the following list of integers: [10, 9, 8, 7, 6, 5, 4, 3, 2, 1]. Show the binary search tree resulting from inserting the integers in the list.

  5. Generate a random list of integers. Show the binary heap tree resulting from inserting the integers on the list one at a time.

  6. Using the list from the previous question, show the binary heap tree resulting from using the list as a parameter to the heapify method. Show both the tree and list form.

  7. Draw the binary search tree that results from inserting the following keys in the order given: 68, 88, 61, 89, 94, 50, 4, 76, 66, and 82.

  8. Generate a random list of integers. Draw the binary search tree resulting from inserting the integers on the list.

  9. Consider the following list of integers: [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]. Show the binary heap resulting from inserting the integers one at a time.

  10. Consider the following list of integers: [10, 9, 8, 7, 6, 5, 4, 3, 2, 1]. Show the binary heap resulting from inserting the integers one at a time.

  11. Consider the two different techniques we used for implementing traversals of a binary tree. Why must we check before the call to preorder when implementing it as a method, whereas we could check inside the call when implementing it as a function?

  12. Show the function calls needed to build the following binary tree.

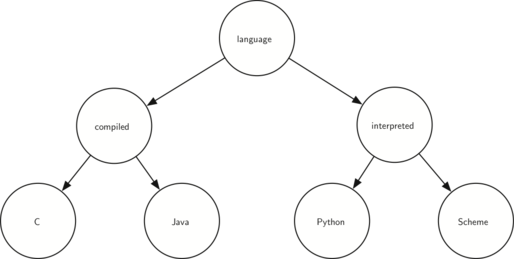
../_images/exerTree.png

  1. Given the following tree, perform the appropriate rotations to bring it back into balance.

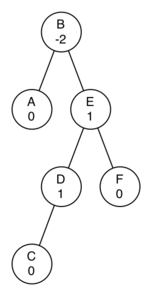
../_images/rotexer1.png

  1. Using the following as a starting point, derive the equation that gives the updated balance factor for node D.

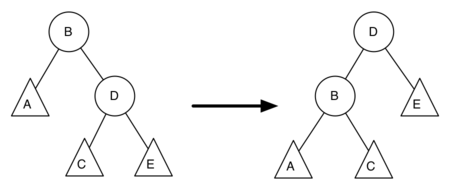
../_images/bfderive.png

  1. Extend the build_parse_tree function to handle mathematical expressions that do not have spaces between every character.

  2. Modify the build_parse_tree and evaluate functions to handle Boolean statements (and, or, and not). Remember that not is a unary operator, so this will complicate your code somewhat.

  3. Using the find_successor method, write a non-recursive inorder traversal for a binary search tree.

  4. A threaded binary tree maintains a reference from each node to its successor. Modify the code for a binary search tree to make it threaded, then write a non-recursive inorder traversal method for the threaded binary search tree.

  5. Modify our implementation of the binary search tree so that it handles duplicate keys properly. That is, if a key is already in the tree then the new payload should replace the old rather than add another node with the same key.

  6. Create a binary heap with a limited heap size. In other words, the heap only keeps track of the n most important items. If the heap grows in size to more than n items the least important item is dropped.

  7. Clean up the print_exp function so that it does not include an extra set of parentheses around each number.

  8. Using the heapify method, write a sorting function that can sort a list in O(nlog⁡n) time.

  9. Write a function that takes a parse tree for a mathematical expression and calculates the derivative of the expression with respect to some variable.

  10. Implement a binary heap as a max heap.

  11. Using the BinaryHeap class, implement a new class called PriorityQueue. Your PriorityQueue class should implement the constructor plus the enqueue and dequeue methods.

  12. Implement the delete method for an AVL tree.