5.5. Converting an Integer to a String in Any Base¶
Suppose you want to convert an integer to a string in some base between
binary and hexadecimal. For example, convert the integer 10 to its
string representation in decimal as "10", or to its string
representation in binary as "1010". While there are many algorithms
to solve this problem, including the algorithm discussed in the stack
section, the recursive formulation of the problem is very
elegant.
Let’s look at a concrete example using base 10 and the number 769.
Suppose we have a sequence of characters corresponding to the first 10
digits, like convString = "0123456789". It is easy to convert a
number less than 10 to its string equivalent by looking it up in the
sequence. For example, if the number is 9, then the string is
convString[9] or "9". If we can arrange to break up the number
769 into three single-digit numbers, 7, 6, and 9, then converting it to
a string is simple. A number less than 10 sounds like a good base case.
Knowing what our base is suggests that the overall algorithm will involve three components:
Reduce the original number to a series of single-digit numbers.
Convert the single digit-number to a string using a lookup.
Concatenate the single-digit strings together to form the final result.
The next step is to figure out how to change state and make progress toward the base case. Since we are working with an integer, let’s consider what mathematical operations might reduce a number. The most likely candidates are division and subtraction. While subtraction might work, it is unclear what we should subtract from what. Integer division with remainders gives us a clear direction. Let’s look at what happens if we divide a number by the base we are trying to convert to.
Using integer division to divide 769 by 10, we get 76 with a remainder of 9. This gives us two good results. First, the remainder is a number less than our base that can be converted to a string immediately by lookup. Second, we get a number that is smaller than our original and moves us toward the base case of having a single number less than our base. Now our job is to convert 76 to its string representation. Again we will use integer division plus remainder to get results of 7 and 6 respectively. Finally, we have reduced the problem to converting 7, which we can do easily since it satisfies the base case condition of \(n < base\), where \(base = 10\). The series of operations we have just performed is illustrated in Figure 3. Notice that the numbers we want to remember are in the remainder boxes along the right side of the diagram.
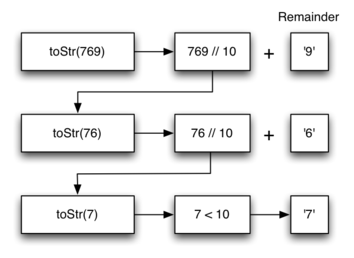
Figure 3: Converting an Integer to a String in Base 10¶
ActiveCode 1 shows the C++ and Python code that implements the algorithm outlined above for any base between 2 and 16.
Notice that in line 7 we check for the base case where n
is less than the base we are converting to. When we detect the base
case, we stop recursing and simply return the string from the
convertString sequence. In line 10 we satisfy both the
second and third laws–by making the recursive call and by reducing the
problem size–using division.
Let’s trace the algorithm again; this time we will convert the number 10
to its base 2 string representation ("1010").
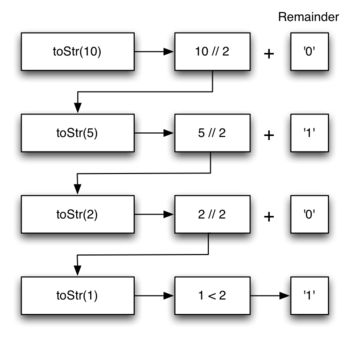
Figure 4: Converting the Number 10 to its Base 2 String Representation¶
Figure 4 shows that we get the results we are looking for,
but it looks like the digits are in the wrong order. The algorithm works
correctly because we make the recursive call first on line
6, then we add the string representation of the remainder.
If we reversed returning the convertString lookup and returning the
toStr call, the resulting string would be backward! But by delaying
the concatenation operation until after the recursive call has returned,
we get the result in the proper order. This should remind you of our
discussion of stacks back in the previous chapter.
Self Check
- A stack, because a recursive function will complete the final function call before any of the other function calls, similar to how a stack has the Last-in-First-out principle.
- Correct! a recursive function will complete the final function call first, because the rest of the calls are waiting for the results of the calls they made.
- A queue, because a recursive function will complete its intial function call before any of the other function calls, similar to how a queue has the First-in-First-out principle.
- Incorrect. Think of it this way, when a function is called and it calls itself, the original function call cannot be completed until the new function call is completed.
Q-3: Is the process of stepping through a recursive function similar to the construct of a stack or a queue?
Write a function that takes a string as a parameter and returns a new string that is the reverse of the old string. Hint: using the substr(strIndex1, strIndex2) method for returning specific sections of a string can help.
Write a function that takes a string as a parameter and returns True if the string is a palindrome, False otherwise. Remember that a string is a palindrome if it is spelled the same both forward and backward. For example: radar is a palindrome. for bonus points palindromes can also be phrases, but you need to remove the spaces and punctuation before checking. for example: madam i’m adam is a palindrome. Other fun palindromes include:
kayak
aibohphobia
Live not on evil
Reviled did I live, said I, as evil I did deliver
Go hang a salami; I’m a lasagna hog.
Able was I ere I saw Elba
Kanakanak – a town in Alaska
Wassamassaw – a town in South Dakota