Loading from URL (In RStudio)
If you’re using RStudio on your computer, you can load the
InfantData.txt file directly from the web using the
url() function:
InfantData = read.table(url("https://www.rossmanchance.com/iscam3/data/InfantData.txt"), header=TRUE)
The
header=TRUE argument indicates the first row contains variable names.
Loading from Your Computer
If you’ve downloaded the
InfantData.txt file, use
file.choose() to browse for it:
InfantData = read.table(file.choose(), header=TRUE)
For This Interactive Textbook (Sage Cell)
Since the Sage cells in this textbook cannot access external URLs, we’ll create the data directly. Click “Evaluate (R)” below to load and view the Infant data:
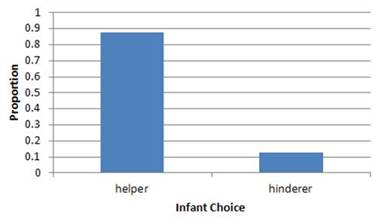
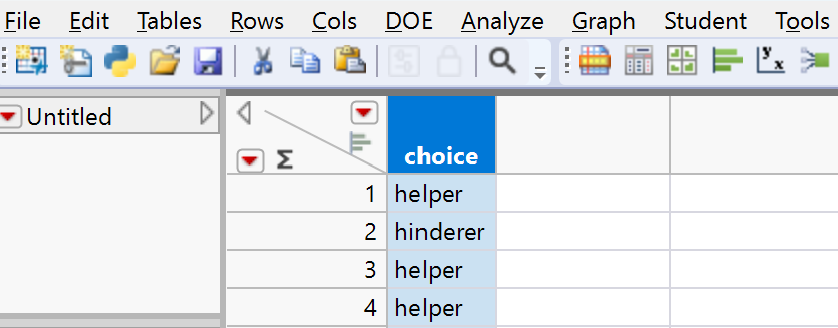
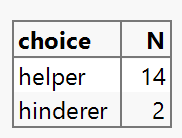
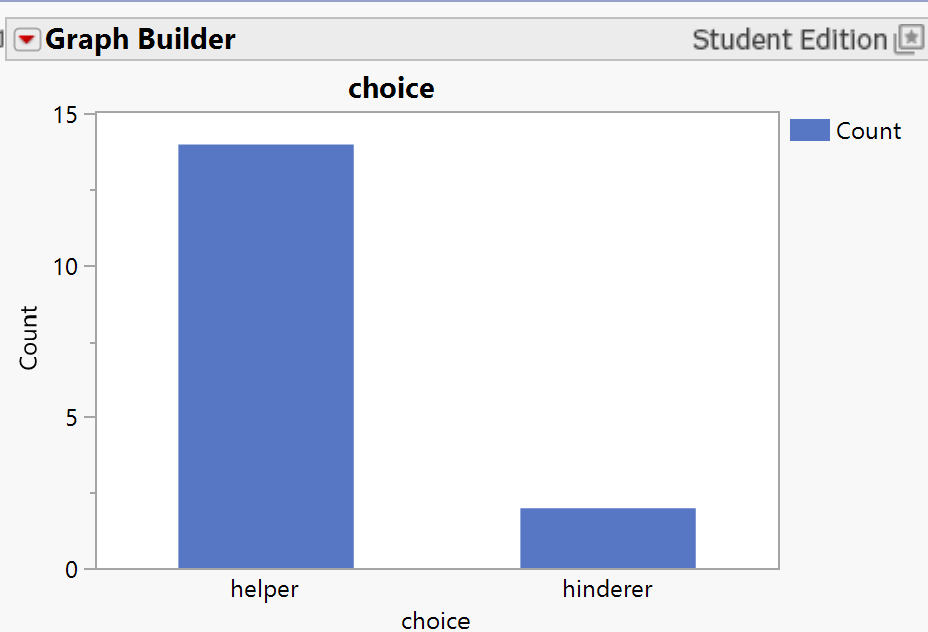
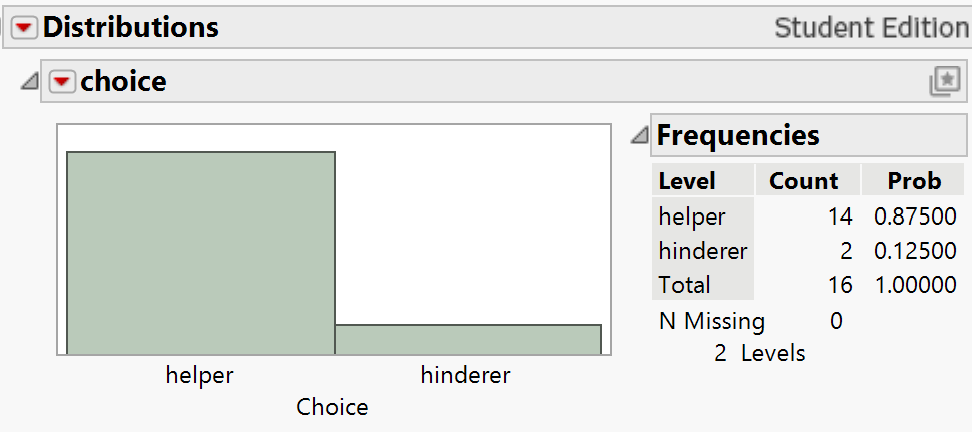
You should see output showing the data with 16 rows and one column called
choice. Verify that you see both "Helper" and "Hinderer" values.
Or you need to clarify to R which datafile you are using (e.g.,
InfantData$choice).
Depending on how the data you are pasting is formatted, you may need additional arguments:
-
sep="\t" - separated by tabs
-
na.strings="*" - how to code missing values
-
strip.white=TRUE - strip extra white space
Solution.
After running
head(InfantData), you should see output similar to:
choice
1 Helper
2 Helper
3 Helper
4 Helper
5 Helper
6 Hinderer
This shows the first 6 observations of the data. The full dataset contains 16 observations total.